Общие закономерности токопрохождения в радиоэлектронных материалах

Основы зонной теории твёрдых тел

Сущность зонной теории сводится к тому, что каждый электрон в одиночном возбужденном атоме находится на определённом дискретном энергетическом уровне, так как энергия квантована.

Электроны располагаются вокруг атома в оболочках, которые состоят из электронов с близкими энергиями. Чем дальше от ядра атома оболочка, тем энергия электрона больше. Самая удалённая оболочка атома называется валентной: в ней находятся электроны, имеющие максимально возможную для данного атома энергию (для связанных электронов). Электроны могут изменять свой энергетический статус: приобретать и терять энергию, переходя при этом из одной электронной оболочки в другую. Электроны могут иметь энергию и большую, чем в валентной оболочке, но при этом они становятся свободными от влияния ядра атома и способными к перемещению в объёме вещества.

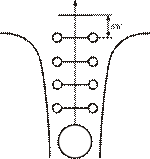
Рисунок 8.

Постулаты зонной теории

I Связанные электроны находятся в потенциальной яме атома.

II Электроны имеют дискретный спектр энергий.

III На каждом энергетическом уровне может одновременно находиться не более двух электронов с разными спиновыми моментами.

Картина, представленная на рисунке 8, деформируется при объединении атомов в кристалл.

Рисунок 9

После сближения отдельных атомов на расстояние межатомного взаимодействия образуется потенциальная диаграмма со слитыми и пониженными границами потенциальной энергии между соседними атомами.

Если температура кристалла не рана 0 К, то расстояние между атомами постоянно изменяется, то есть, атомы колеблются. Поэтому в каждый фиксированный момент времени немного отклоняется от изображённой на рисунке 9. При сближении атомов энергия потенциального барьера между ними понижается, а при удалении – повышается. При образовании кластера, состоящего из двух атомов, электронные оболочки этих атомов взаимодействуют между собой, частично перекрываются, при этом фактически возникает ситуация, когда в одной точке пространства находятся уже не 2, а 4 электрона с одинаковой энергией, что противоречит постулату III. Следовательно, при образовании кластера каждый энергетический уровень расщепляется на 2 близко лежащих по оси энергии подуровня. При присоединении третьего – на 3, и так далее. Если мы имеем 1 см³ кристаллического вещества, то каждый энергетический уровень будет расщеплён 10²² – 10²³ подуровней (по числу атомов), расстояние между ними находится в пределах 10^-16 – 10^-25 эВ.

[ 1 электрон-вольт – энергия, необходимая для перемещения 1 электрона в электрическом поле с напряжённостью 1 вольт]

Энергия 10^-25 эВ пренебрежимо мала, поэтому считается, что в кристалл каждый энергетический уровень расщепляется в квазисплошную разрешённую для пребывания электронов энергетическую зону.

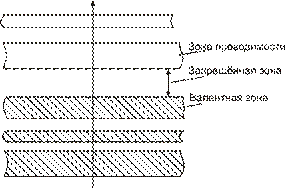
Рисунок 10.

Рисунок 11.

Условия возникновения и понятие об активационном характере токопрохождения

Существует две причины возникновения макротоков в материалах:

1. Градиент потенциала ;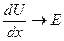

2. Градиент концентрации .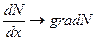

В соответствии с этими причинами электрический ток, возникающий под действием градиента потенциала называется дрейфовым, по действием концентрации – диффузионный.

Условия, необходимые для возникновения макротоков:

1. Наличие свободных носителей заряда: электронов, ионов, активных в зарядовом отношении радикалов.

2. Способность носителей заряда к перемещению, то есть подвижность.

Как для образования свободного носителя заряда, так и для начала его движения требуется какая-то энергия, причём всегда. Принято различать эти энергии: энергия, необходимая для образования одного свободного носителя заряда – энергия активации носителя заряда; энергия, необходимая для перемещения – энергия активации подвижности.

В том случае, если величина этих энергий пренебрежимо мала, говорят, что имеет место безактивационный механизм образования носителей заряда и подвижности (электропроводности)

Материалы	Механизм образования	Механизм подвижности
Металлы	безактивационный	безактивационный
Полупроводники	активационный	безактивационный
Диэлектрики	активационный	активационный
Электролиты	безактивационный	активационный

Чисто безактивациооный механизм электропроводности имеют только металлы. Остальные классы веществ имеют электропроводность активационного типа.

Не вдаваясь в механизм движения носителей заряда, очевидно 6электрический ток равен произведению числа носителей заряда на их подвижность: .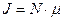

Подвижность носителей заряда.

В соответствии с существующими причинами возникновения электрического тока, различают дрейфовую и диффузионную подвижности.

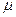- дрейфовая подвижность – скорость направленного движения носителя заряда в результате воздействия на него внешнего электрического поля с напряжённостью 1В/см. Размерность .

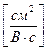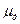- диффузионная подвижность – скорость направленного движения носителя заряда под действием единичного градиента концентрации. Размерность .

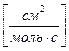Рассмотрим, как зависит подвижность от атомарной структуры вещества (материала) и характера токопрохождения. Для описания дрейфовой подвижности применимы две модели: пролётная и прыжковая.

Пролётная модель применима к веществам, для которых существует понятие длины свободного пробега. Графически можно представить

Рисунок 12.

В движении электронов при наличии Е≠0 возникает отклонение от прямолинейности движения – параболическая траектория движения. При этом очевидно, что направленность всему движению придаёт именно это отклонение в сторону действия электрического поля.

Для дальнейшего изучения нам потребуются следующие понятия:

· длина свободного пробега λ;

· средняя скорость теплового движения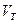

· средняя скорость направленного движения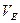

Допущение: энергия направленного движения носителя заряда гораздо меньше тепловой энергии:

.

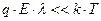Следовательно 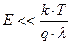, то есть мы говорим о слабых электрических полях.

Согласно допущению очевидно, что

,

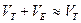то есть приращение скорости, обусловленное действием электрического поля, незначительно.

Для расчёта подвижности необходимо оценить расстояние, которое носитель заряда проходит за одну секунду.

Среднее время пролёта между соударениями

.

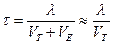Тогда количество соударений в 1 секунду

.

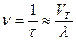За время свободного пролёта носитель под действием электрического поля направленно смещается на расстояние N₁:

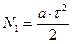, где а – коэффициент, .

.

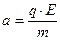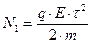Учитывая элементарных перемещений в одну секунду можно сказать, что

,

,

, .

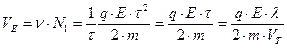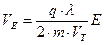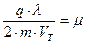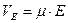Поскольку

,

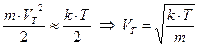итоговое выражение для подвижности примет вид:

.

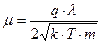Из него следует два вывода:

1. Дрейфовая подвижность не зависит от величины напряжённости электрического поля.

2. Истинная скорость носителя заряда при любых напряжённостях может быть определена по формуле:

.

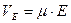Данное выражение является проявлением закона Ома для микромира.

Прыжковая модель

Применима для описания движения носителей заряда, при котором теряет смысл понятие длина свободного пробега.

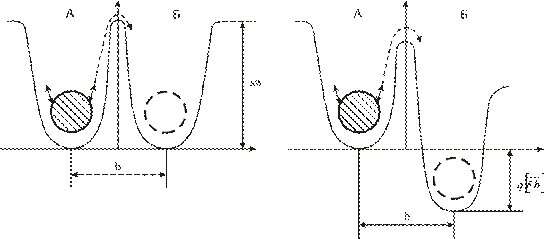
Рисунок 13.

Как и в предыдущей модели, введём ограничение:

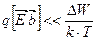, что говорит о том, что модель справедлива лишь для малых электрических потерь.

1. Электрическое поле не способно непосредственно перенести носитель заряда из одного положения в другое.

2. Электрическое поле только нарушает симметрию потенциальных диаграмм. Следовательно, вероятности нахождения заряда в различных положениях различны.

3. Носитель заряда совершает колебательные движения в положении равновесия с частотой 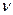и только благодаря тепловой флуктуации способен приобрести энергию, достаточную для преодоления энергетического барьера, то есть для перехода из одного равновесного состояние в другое.

4. Направленное движение будет обусловлено неодинаковой частотой прыжков вправо и влево, что обусловлено разной высотой энергетических барьеров.

Влево: 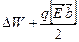, вправо: 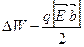. Из этого следует, что скорости перемещения вправо и влево 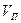и 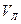будут различными и очевидно, что скорость направленного движения будет представлять собой сумму этих скоростей:

.

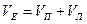Оценим её величину. Носитель заряда совершает 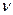колебаний в одну секунду, то есть принимает 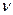попыток преодолеть барьер. Обозначим 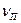и 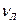- число удачных попыток преодолеть соответственно правый или левый барьер.

;

.

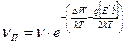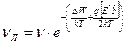Тогда разница 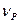определит количество элементарных шагов направленного движения носителя в единицу времени:

.

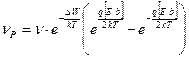Необходимо разложить полученное выражение в ряд. Используем допущение, которое мы приняли в начале – о малости энергии электрического поля и разложим экспоненты в ряд с ограничением двумя членами разложения:

.

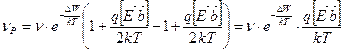Поскольку величина каждого шага составляет b, то скорость насителя

.

.

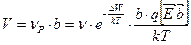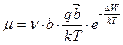Из полученной зависимости можно сделать выводы:

1. Скорость направленного движения (подвижность) не зависит от напряжённости электрического поля.

2. Истинная скорость вычисляется по формуле:

.

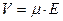Диффузионная подвижность носителей заряда.

Предположим, что в материале искусственно поддерживается градиент концентрации вида:

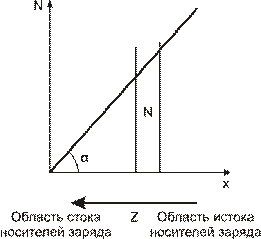
Рисунок 14.

Возникает поток Z.

,

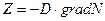где D – коэффициент диффузии, 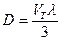. Знак минус в выражении говорит о том, что диффузия идёт в сторону уменьшения концентрации.

Отсечём на графике слой вещества с толщиной 1см и со средней концентрацией носителей заряда N и введём понятие средней диффузионной скорости носителя:

;

;

;

.

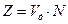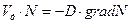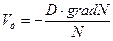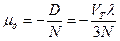Из полученной зависимости можно сделать вывод:

В отличии от дрейфовой подвижности, диффузионная зависит от причины, вызывающей направленное перемещение носителей заряда, то есть от концентрации. Чем меньше концентрация, тем скорость диффузионного движения больше.

Количество носителей заряда.

Для безактивационного механизма образования носителей заряда, который имеет место в металлах и электролитах. Энергия, необходимая для активации, мала (10^-19эВ). Поэтому в них число носителей заряда определяется в основном количеством атомов в единице объёма.

Что касается активационного механизма образования носителей заряда, то здесь существует другая система подсчёта, которая опирается на квантовую статистику. Предположим, что для образования носителей необходимо затратить энергию 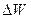. Количество нейтральных атомов и молекул, которые могут быть превращены в ионы составляет N₀ в 1см³. Тогда без учёта процесса гибели носителей заряда число атомов, которые могут претерпеть акт ионизации N будет определяться:

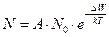, где А – коэффициент пропорциональности, зависит от материала (1…3).

;

.

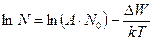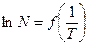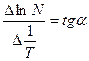
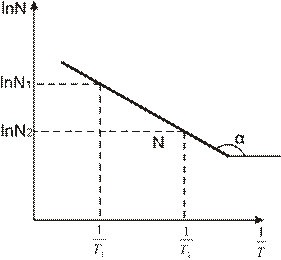
Рисунок 15.

Возьмём на этой прямой 2 точки

;

; ;

.

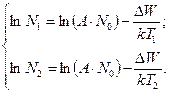
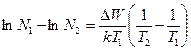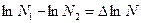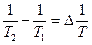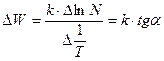Зависимость изменения концентрации носителей заряда от температуры, построенная в логарифмических координатах, определяет величину энергии ионизации данного материала через угол наклона данной прямой.

[Для полупроводников 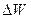- ширина запрещённой зоны]

Вывод основного уравнения электропроводности вещества.

Макроскопический подход

Рассмотрим опыт по схеме, изображённой на рисунке 16.

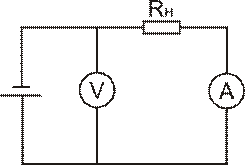
Рисунок 16.

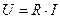, где R – коэффициент пропорциональности сопротивления цепи.

Из опыта известно:

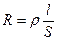, где 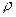- коэффициент пропорциональности, удельное сопротивление.

Введём искусственно ещё одну величину:

- удельная проводимость.

Вывод: R, 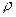и 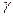- экспериментально измеряемые величины опыта, которые не дают представления о природе токопрохождения и не раскрывают взаимосвязь между величиной тока и структурой вещества.

.

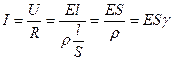Микроскопический подход

Рассмотрим процесс прохождения тока с молекулярно-атомарной позиции.

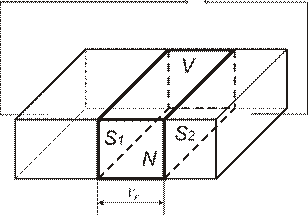
Рисунок 17

Предположим, что в 1 см³ данного проводника находится N носителей заряда. Они перемещаются по проводнику со средней скоростью направленного движения 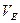. При этом очевидно, что в течении одной секунды через любое сечение проводника пройдёт количество зарядов, находящееся с объёме между двумя сечениями, отстоящими друг от друга на расстояние, равное .

.

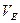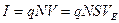Согласно результатам, полученным в разделе, посвящённом подвижности, -

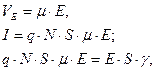
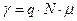- основное уравнение электропроводности вещества.

В этом случае, если в материале имеется не один тип носителей заряда, а n –

.
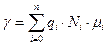