Фізичні основи низькочастотних індукційних методів

Вирішення прямої задачі індукційних методів полягає в отриманні залежності виміряної е.р.с. електромагнітного поля від електропровідності середовища, його геометрії та параметрів зонда.

Наближена теорія низькочастотного індукційного методу вперше була розроблена Х. Г. Доллем в 1949 р., потім вона отримала розвиток в роботах С. М. Аксельрода, А. А. Кауфмана та інших дослідників. В основі наближеної теорії Долля лежать два припущення: 1) всі індуковані в навколишньому середовищі вихрові струми мають одну і ту саму фазу, зсунуту відносно фази струму в генераторній котушці на 90°; це означає, що взаємодія вихрових струмів відсутня, тобто при вирішенні прямої задачі явище скін-ефекту не береться до уваги; 2) амплітуда щільності струму в будь-якій точці середовища розраховується за спрощеною формулою і визначається тільки просторовим фактором та питомою електропровідністю ділянки середовища.

Іншими словами, в основі наближеної теорії Доля лежить припущення про те, що при досить високому питомому опорі порід та низький частоті електромагнітного поля можна знехтувати взаємодією струмів, що індукуються в провідному середовищі. Тому фаза струмів є постійною і складає 90º на будь-якій відстані від генераторної котушки, і сигнал, що вимірюється, є сумою окремих сигналів, утворених різними ділянками середовища. При чому кожен доданок являється функцією тільки питомої провідності окремої ділянки. Формули, отримані на основі цієї теорії, є асимптотичними. Вони є справедливими при хвилях великої довжини у порівнянні з радіусом свердловини, потужністю пласта та діаметром зони проникнення.

Ці припущення є справедливими лише тоді, коли частота струму живлення та електропровідність середовища порівняно невеликі. При високій частоті струму або великій електропровідності порід явище скін-ефекту суттєво змінює характер розподілення електромагнітного поля, і в цьому випадку при вирішенні прямої задачі необхідно використати строгу теорію.

Наближена теорія низькочастотних індукційних методів дозволяє порівняно просто встановити залежність ефективної питомої електропровідності досліджуваного середовища від електропровідності окремих його складових, їх розмірів і положення відносно індукційного зонда, а також наочно представити фізичну сутність цього методу. За допомогою наближеної теорії можливо шляхом елементарних розрахунків вирішити пряму задачу індукційного методу для випадку плоских та циліндричних поверхонь розділу між середовищами.

Отже, розглянемо однорідне ізотропне середовище питомої електропровідності σ, абсолютної діелектричної проникності ε_а та магнітної проникності μ_а.

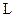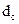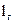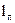На вісі свердловини розташований індукційний зонд, складений двома котушками – генераторної та приймальної (вимірювальної), розташованих на відстані одна від одної. Вплив свердловини в даній постановці не враховується ( → 0). Генераторна та вимірювальна котушки мають відповідно висоти та з кількістю витків 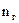та 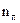, радіуси яких 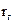та 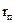. Площа одного витку генераторної котушки 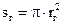, а вимірювальної – 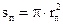; загальні площі витків, відповідно, 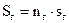та 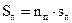. Домовимося, що 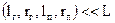. Це припущення дозволяє розглядати котушки як точкові. Генераторну котушку можна замінити для спрощення розрахунків магнітним диполем зі змінним моментом.

Генераторна котушка живиться змінним струмом з амплітудою 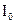, миттєве значення якого

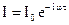, (52)

де 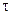– час; 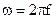– кругова частота; 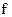– циклічна частота.

Згаданий вище магнітний диполь утворює в навколишньому середовищі електромагнітне поле. Необхідно визначити величину е.р.с., що наводиться вихровим струмом у досліджуваному середовищі, та встановити зв’язок між величиною наведеної е.р.с. та питомою електропровідністю однорідного середовища, частотою поля і параметрами зонда: 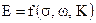, де 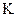– коефіцієнт індукційного зонду.

Для розв’язку задачі введемо циліндричну систему координат 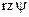, початок якої розташований в точці О, що являється серединою відстані між центрами генераторної та вимірювальної котушок. Розіб’ємо весь досліджуваний простір на елементарні тороїди, що являють собою ділянки породи, обмежені горизонтальними та коаксіально-циліндричними поверхнями. Одиничний тороїд – це горизонтальне кільце радіуса 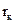з центром на осі свердловини (рис. 38) та площею його прямокутного перерізу 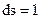. Він названий Х.Г. Доллем елементарним кільцем.

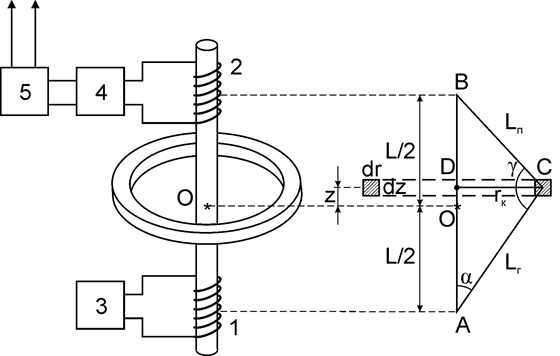
Рис. 38. Геометрична модель елементарного кільця: О – середина індукційного зонда (точка запису); D – центр елементарного кільця; z = OD; r_к – радіус елементарного кільця; ds = dr×dz – площа елементарного кільця; 1 – генераторна котушка; 2 – вимірювальна котушка; 3 – генератор; 4 – підсилювач; 5 – фазочутливий випрямляч.

З урахуванням (52) магнітний момент магнітного диполя запишеться:

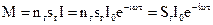(53)

Магнітний диполь утворює в навколишньому середовищі магнітне поле напруженістю

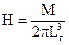(54)

де 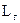– відстань від центру генераторної котушки до довільної точки, розташованої на тороїді радіусу 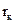(точка С на рис. 38)

Беручи до уваги (53),

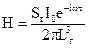(55)

Як відомо, величина магнітного потоку, що пронизує замкнену поверхню,

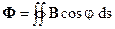, (56)

де 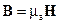– вектор магнітної індукції; 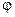– кут між нормаллю до поверхні тору і силовими лініями магнітного поля.

Для елементарного кільця з радіусом 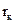, площу якого магнітні силові лінії перетинають під кутом 90 ^º ( 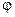= 0^º), формула (56) має вигляд:

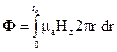, (57)

де 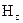– вертикальна компонента напруженості магнітного диполя (оскільки силові лінії магнітного поля направлені вздовж вісі свердловини, ).

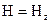Підставивши (55) в (57) і провівши інтегрування, отримаємо

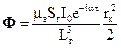(58)

Зміни магнітного потоку 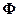в часі утворює е.р.с. електромагнітної індукції 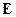в елементарному кільці (згідно закону електромагнітної індукції Фарадея):

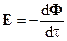(59)

Знак мінус в формулі (59) відповідає закону Ленца, згідно якого індукційний струм, взаємодіючи з магнітним полем, викликає силу, спрямовану протилежно дії магнітного диполя.

Взявши похідну у відповідності з (59) від (58), маємо

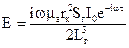(60)

Внаслідок дії е.р.с. в одиничному елементарному кільці виникає вихровий струм силою

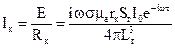, (61)

де 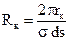– опір одиничного елементарного кільця; 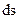– площа його перерізу, що дорівнює 1.

Струм, що протікає в елементарному кільці, утворює в навколишньому просторі вторинне магнітне поле. У відповідності з (54) в точці, де розташована приймаюча котушка, напруженість 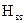цього поля

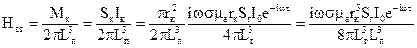, (62)

де: 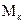– магнітний момент елементарного кільця радіуса 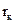і площею 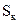; 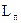– відстань від точок елементарного кільця до центру приймаючої котушки;

Величина вторинного магнітного потоку, що пронизує витки приймаючої котушки,

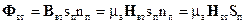(63)

Підставивши вираз (62) у вираз (63), отримаємо

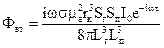(64)

Зміна вторинного магнітного потоку в часі утворює у вимірювальній котушці е.р.с.

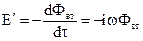(65)

З врахуванням виразу (64) і співвідношення 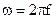е.р.с. у приймальній котушці буде:

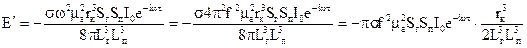(66)

Знак мінус в (66) свідчить про те, що активна складова е.р.с., індукована вторинним магнітним полем в приймальній котушці, знаходиться у протифазі із струмом, що живить генераторну котушку.

Одночасно із вторинною е.р.с., що викликається вихровим струмом у елементарному кільці (досліджуваному середовищі) і є корисним сигналом, в приймальній котушці наводиться е.р.с прямого поля генераторної котушки, що не містить інформації про досліджуване середовище, тобто є завадою. Зазвичай, як було сказано раніше, вона вилучається апаратними засобами безпосередньо в процесі вимірів.

Таким чином, в загальному випадку зареєстрована е.р.с. залежить: від питомої провідності 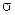та магнітної проникності 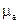середовища, від конструктивних особливостей зонду ( 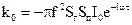) та від взаємного розташування зонду і досліджуваного середовища ( 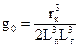). Останній вираз, за Доллем, називається геометричним фактором елементарного кільця, або диференціальним геометричним фактором .

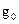Абсолютна магнітна проникність більшості осадових гірських порід фактично не відрізняється від магнітної проникності вакууму ( 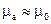). Тому у виразі (66) її можна вважати сталою. Таким чином, сигнал, що створюється елементарним кільцем породи, є пропорційним питомій провідності елементарного кільця 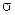та його геометричному фактору 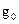. Для того, аби обрахувати сигнал від усього середовища, що оточує зонд, представимо функцію 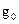в циліндричних координатах 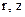. Для цього відстані від генераторної та приймальної котушок до точки спостереження також виразимо через :

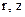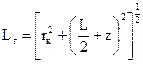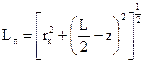, (67)

Тоді, диференціальний геометричний фактор запишеться наступним чином:

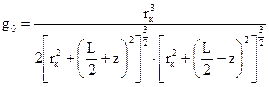(68)

Знаючи сигнал, створений одним елементарним кільцем породи, можна розрахувати сигнал, що створюється усім оточуючим простором, який буде дорівнювати сумі сигналів елементарних кілець породи, тобто потрібно проінтегрувати вираз (68) за двома координатами r та z. Оскільки середовище є однорідним ( 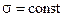), то сумарний сигнал буде:

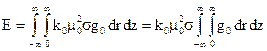(69)

Зауважимо, що до конструктивних особливостей зонду відноситься і довжина зонду L, від якої безпосередньо залежать глибинність і роздільна здатність досліджень. Вочевидь, розмір зонду повинен визначати таку важливу характеристику, як коефіцієнт зонду 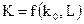. Тому Доллем запропоновано одночасно помножити і розділити вираз (69) на величину L. Такий суто технічний прийом, з одного боку, дозволяє звести інтегральне значення просторового фактору G усього однорідного середовища до безрозмірної величини, що дорівнює одиниці (шляхом заміни 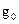на функцію ):

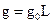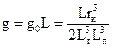(70)

а з іншого – дозволяє визначити коефіцієнт зонда ( ):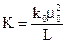

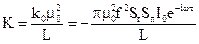(71)

В останньому виразі параметр 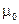був введений до коефіцієнту зонду, оскільки, як було зазначено вище, абсолютна магнітна проникність осадових порід не відрізняється від магнітної проникності вакууму і залишається фактично константою.

Тоді, вираз (69) перепишеться у вигляді:

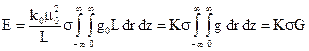(72)

Як було зазначено вище, для однорідного середовища просторовий фактор

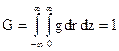(73)

Тоді, питома провідність такого середовища визначиться:

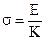(74)