Основные типы кристаллических структур

Способы описания и изображения атомного

Строения кристалла

Кристаллы

Периодичность структуры является наиболее характерным свойством кристаллов. В периодической решетке всегда можно выделить элементарную ячейку, транслируя которую в пространстве легко получить представление о структуре всего кристалла. Образование каким-либо элементом или соединением определенной пространственной решетки в основном зависит от размеров атомов и электронной конфигурации их внешних оболочек.

Русский ученый Е. С. Федоров почти за 40 лет до того, как были найдены методы рентгеноструктурного анализа, рассчитал возможные расположения частиц в кристаллических решетках различных веществ и предложил 230 пространственных гпупп. Геометрически возможны лишь 14 различных пространственных решеток, получивших название решеток Браве и являющихся основой шести кристаллических систем, приведенных в табл. 2.1 и на рис. 2.1. Иногда считают ромбоэдрическую, или тригональную, систему (а = b = с; α = β = γ ≠ 90°) самостоятельной седьмой системой.

Если атомы расположены только в вершинах элементарной ячейки, то решетка называется примитивной или простой. Если атомы есть и на гранях или в объеме ячейки, то решетка будет сложной (например, базо-, объемо- и гранецентрированной).

Кристаллические тела могут быть в виде отдельных крупных кристаллов — монокристаллов или состоять из совокупности большого числа мелких кристалликов (зерен).

Таблица 2.1

Пространственные решетки кристаллических систем

Кристалличе- ская система	Пространственная решетка	Соотношение между осевыми углами и осевыми единицами
1. Триклинная	I – простая	a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90°
2. Моноклинная	II – простая III – базоцентрированная	a ≠ b ≠ c; α = γ = 90°; β ≠ 90°
3. Ромбическаяили орторомбическая	IV – простая V – базоцентрированная VI – объемноцентрированная VII – гранецентрированная	a ≠ b ≠ c; α = β = γ = 90°
4. Гексагональная	VIII – простая IX – ромбоэдрическая	a = b ≠ c; α = β = 90°; γ = 120°
5. Тетрагональная	X – простая XI – объемноцентрированная	a = b ≠ c; α = β = γ = 90°
6. Кубическая	XII – простая XIII ‑ объемноцентрированная XIV – гранецентрированная	a = b = c; α = β = γ = 90°

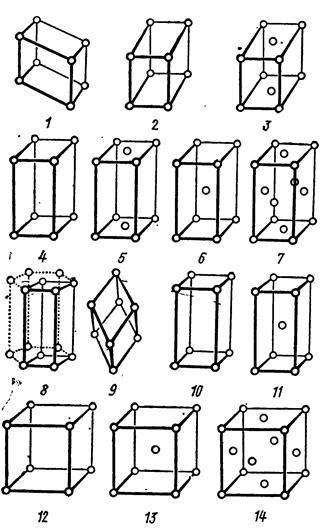
Рис. 2.1. Решетки Браве

В случае поликристалла в пределах каждого зерна атомы расположены периодически, но при переходе от одного зерна к другому на границах раздела регулярное расположение частиц нарушается.

Монокристаллы характеризуются анизотропией свойств. В поликристаллических телах анизотропия в большинстве случаев не наблюдается, однако с помощью специальной обработки могут быть получены текстурованные материалы с ориентированым расположением кристаллов.

Так как монокристаллы анизотропны, то при определении электрических, механических и других свойств необходимо указывать расположение кристаллографических плоскостей и направления в кристаллах. Для этого используют индексы Миллера.

Индексы Миллера

Пусть плоскость отсекает на осях координат отрезки ОА, ОВ и ОС (в единицах периода решетки). Рассчитаем обратные им величины H = 1/ОА, K = 1/ОВ, L = 1/ОС и определим наименьшие целые числа с таким же соотношением, как H : K : L = h : k : l. Целочисленные (hkl) называются индексами Миллера плоскости.

В кубических кристаллах индексы (100) относятся к плоскости, параллельной осям У и Z; индексы (010) — к плоскости, параллельной осям X и Z, а (001) — к плоскости, параллельной осям X и Y. В кристаллах с ортогональными осями эти плоскости вместе с тем перпендикулярны соответственно осям X, Y и Z.

Для обозначения направлений в кристалле применяют индексы в виде наименьших целых чисел, относящихся между собой как компо­ненты вектора, параллельного данному направлению. В отличие от обозначения плоскостей их пишут в квадратных скобках. В кубических кристаллах эти направления перпендикулярны плоскости с теми же индексами. Положительное направление оси X обозначают [100], положительное направление оси Y — [010], отрица­тельное направление оси Z — [001], диагональ куба — [111] и т.д. Обозначения кристаллографических плоскостей и направлений приведены, на рис. 2.2.

Плоскости, отсекающие равные отрезки, но расположенные в других октантах, эквивалентны в кристаллографическом и физико-химическом отношениях. Они образуют совокупность эквивалентных плоскостей – {hkl} или систему плоскостей, у которых h, k, l могут быть записаны в любом порядке и с любым числом минусов перед индексами. Минус записывается над индексом.

Положение направления в пространственной решетке может быть легко определено координатами атома, ближайшего к началу координат и лежащего на данном направлении.

Совокупность эквивалентных направлений или система направлений обозначается <hkl>, где h, k, l могут быть записаны в любом порядке и с любым числом минусов: <100> ‑ совокупность направлений, параллельных всем ребрам куба; {100} ‑ совокупность плоскостей, параллельных всем граням куба.

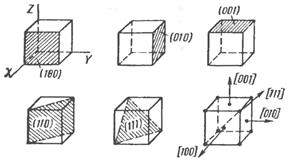
Рис. 2.2. Примеры обозначения кристаллографических

плоскостей и направлений в кубических кристаллах

с помощью индексов Миллера

Примеры решения задач

Пример 1. Определить индексы плоскости, отсекающей на осях решетки отрезки А = 1, В = 2, С = - 4.

Отношения величин, обратных отрезкам, 1/А : 1/В : 1/С = 1/1 : 1/2 : 1/(-4). Доводим это отношение до отношения трех целых чисел, умножая на общий знаменатель 4, дополнитель­ными множителями будут 4 и 2. 1/А : 1/В : 1/С = 4 : 2 :(- 1). Это и будут искомые h, k, l. Индексы плоскости (42 ).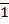

Пример 2. Определить отрезки, которые отсекает на осях решетки плоскость (023).

Записываем величины, обратные индексам плоскости: 1/0, 1/2, 1/3. Умножаем на общий знаменатель, равный 6 (доводим отрезки до целых чисел). Отрезки, отсекаемые плоскостью на осях, будут равны А = 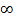, В = 3, С = 2. Эта плоскость будет параллельна оси х, так как А = .

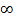Полиморфизм

Некоторые твердые вещества обладают способностью образовывать не одну, а две и более кристаллические структуры, устойчивые при различных температурах и давлениях. Такое свойство материалов называют полиморфизмом, а отвечающие им кристаллические структуры называют полиморфными формами или аллотропными модификациями вещества.

Модификацию, устойчивую при нормальной и более низкой температуре, принято обозначать буквой α; модификации, устойчивые при более высоких температурах, обозначают соответственно буквами β, γ и т.д.

Полиморфизм широко распространен среди технических материалов и имеет важное значение для их обработки и эксплуатации.

Классическим примером полиморфизма является низкотемпературное пре­вращение белого олова (β-Sn) в серое (α-Sn), известное в технике как «оловянная чума».

Практический интерес представляет полиморфизм углерода — существование его в виде алмаза или графита. В обычных условиях графит является более устойчивой модификацией, чем алмаз. Однако при повышении давления устойчивость алмаза растет, а графита падает, и при достаточно высоких давлениях алмаз становится более устойчивым. Если при этом повысить температуру, чтобы увеличить подвижность атомов, то графит можно перевести в алмаз. На этом принци­пе основано получение искусственных алмазов. В Советском Союзе их промышленное производство началось в 1961 г. Синтез проводят под давлением порядка 10¹⁰ Па при температуре на уровне 2000 °С. Получаемые таким образом искусственные алмазы имеют более высокую прочность и твердость, нежели природные кристаллы.

2.1.5. Изоморфизм

Изоморфизм – это свойство химически и геометрически близких атомов и ионов и их сочетаний замещать друг друга в кристаллической решетке, образуя кристаллы переменного состава.

Изоморфные кристаллы кремния и германия образуют непрерывный ряд твердых растворов замещения. Оба этих вещества кристаллизуются в структуре алмаза, период решетки германия а = 0,565 нм, кремния а = 0,542 нм, различие в периодах составляет менее 4 %, поэтому возможно образование образование твердых растворов замещения с неограниченной растворимостью, в которых атомы германия и кремния располагаются в узлах алмазной решетки.

Плотность, период решетки, твердость в изоморфном ряду смешанных кристаллов Si – Ge меняются линейно. Подбором различных изоморфных составов удается варьировать области рабочих температур и электрофизические параметры для этих и других твердых растворов полупроводниковых соединений.