Статистический характер второго закона термодинамики

Химическая термодинамика изучает системы реагирующих веществ, состоящих из очень большого числа частиц. В подобных системах различают так называемые макро и микропараметры. К макрохарактеристикам относятся независимые переменные, свойственные системе в целом, например давление (р), объем (V), температура (Т), концентрации (С_i), которые можно определить экспериментально или рассчитать теоретически. Наряду с этим каждая частица имеет свои непрерывно изменяющиеся микрохарактеристики: координаты в пространстве (X_i, Y_i, Z_i), скорость перемещения по свеем трем направлениям (V_х,_i; V_y,_i; V_z,_i;), энергию. Совокупность микропараметров каждой частицы называется микросостоянием частицы. Число микросостояний, посредством которых реализуется данное макросостояние системы, называется термодинамической вероятностью (W). В отличии от математической вероятности, равной единице или меньше ее, термодинамическая вероятность представляет собой очень большую величину: значение W имеет порядок 10⁴ для системы, состоящей всего из десятка частиц, в то время один моль вещества содержит W_А = 6,02 * 10²³ структурных единиц.

Чтобы перейти к более удобным для восприятия и расчетов числам, в термодинамике используют не величину W, а ее логарифм. Связь энтропии с термодинамической вероятностью установил Л.Больцман и соответствующее уравнение названо его именем.

S = k lgW (1.53)

Где К = 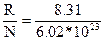= 1,38 * 10^-23 Дж/К – константа Больцмана (универсальная газовая постоянная, рассчитанная на одну молекулу).

Так как энтропия является экстенсивным свойством системы, поэтому ее целесообразно относить к одному молю вещества и выражать

S = R lgW Дж/моль*К (1.54)

Из уравнения (1.54) видно, что энтропия системы увеличивается пропорционально логарифму термодинамической вероятности.

Рассмотрим изолированную систему, в которой находятся два химически не взаимодействующих газа. Например, азот (N₂) и аргон (Ar), при одинаковых температуре и давлении разделенные перегородкой. (Рис.1.10а).

В этом состоянии термодинамическая вероятность системы равна W₁ (Рис. 1.10б)

Р, Т, U, V = const

а

б

Рис. 1.10 Схема смешивания двух химически невзаимодействующих газов.

При удалении перегородки газы начнут самопроизвольно диффундировать друг в друга (смешиваться) до тех пор, пока молекулы каждого газа не распределятся по всему объему. В конечном состоянии термодинамическая вероятность равна W₂. Система самопроизвольно перешла из мене вероятного состояния в более вероятное (W₁ > W₂). Энергетический обмен системы отсутствует, следовательно, единственной причиной протекания данного процесса является увеличение энтропии:

_∆S = S₂ – S₁ = R lgW₂ - R lgW₁ = R lg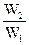

По W₂ > W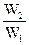₁; > 1; 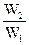> 0, следовательно, _∆S > 0

Таким образом, в соответствии с уравнением (1.54) второй закон термодинамики можно сформулировать так, всякая изолированная система самопроизвольно стремиться принять состояние, характеризующееся максимальной термодинамической вероятностью.

Термодинамическая вероятность напрямую связана со степенью беспорядка в расположении частиц системы.

Представим себе какое-либо твердое вещество (например кристалл C_sF), которое находится при данных Р и Т.Ионы цезия (C_s⁺) и фтора (F^-), расположенные в узлах кристаллической решетки, совершают колебания около равновесных положений. Представим себе, что мы могли бы так быстро «фотографировать» этот кристалл, что фиксировали мгновенные положения колеблющихся ионов. Тогда количество неодинаковых фотоснимков равнялось бы W. В условиях более низких температур амплитуда колебания этих частиц уменьшается и число не совпадающих фотоснимков сокращается, а это значит, что величина W станет значительно меньше.

Допустим, что наш кристалл взят при Т = 10 К; тогда термодинамическая вероятность станет совсем незначительной. И, наконец, если бы достигли Т = 0 К, то обнаружили бы, что все ионы «вмерзли» в узлы кристаллической решетки, т.е. вариации в осуществлении данного состояния были бы исключены, иными словами W = 1. В соответствии с уравнением (1.54), это значит, что при Т =0 К энтропия равна нулю (S = 0).

Мысленно осуществив обратный процесс, приходим к выводу, что нагревание вызовет возрастание энтропии.

Изложенное означает, что энтропия является мерой неупорядоченности состояния системы – мерой беспорядка.

Это и нагревание вещества, и его плавление, кипение и сублимация, превращение кристаллического вещества в аморфное; это и растворение газа, и растворение соли, и многие другие процессы, протекающие с увеличением объема.

Все изменения, противоположные перечисленным, в том числе и химические реакции, сопровождающиеся уменьшением объема, например, полимеризация, являются энтропийно дефицитными – идут с уменьшением энтропии.

Возрастание энтропии вещества при повышении температуры можно проиллюстрировать на рис 1.11

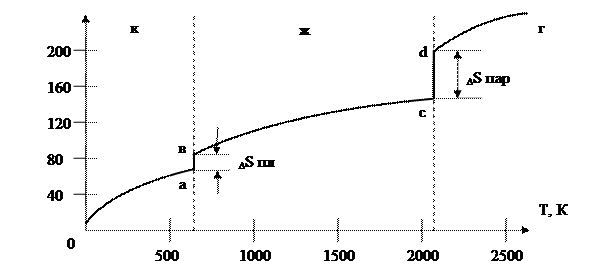Рис. 1.11 Зависимость энтропии свинца от температуры.

_∆S_пл = S^ж – S^к = 8 Дж/ моль * К

_∆S_пар = S^г – S^ж = 88 Дж/ моль * К

Т_пл = 600,5 К

Т_кип = 2013 К

Влияние давления на энтропию можно показать на следующем примере:

при Т = 500 К и р = 101,3 кПа энтропия аммиака

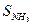= 212 Дж/ моль * К, а

при Т = 500 К и р = 30,300 кПа

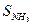= 146 Дж/ моль * К

Чтобы энтропии веществ можно было сопоставлять и определять изменение в различных процессах, их, как и энтальпии образования и тепловые эффекты, относят к определенным условиям. Энтальпию при давлении р = 101,3 кПа обозначают S⁰_(Т) и называют стандартной. Но так как энтальпия каждого вещества возрастает с температурой в расчетах пользуются значениями энтропии при стандартной температуре (Т = 298 К) – S⁰₂₉₈.