Нестационарное уравнение Шредингера.
Выше мы уже отмечали, что модели Бора и Бора – Зоммерфельда, являющиеся полуклассическими по своей сути, не могут описать особенности динамики атомных электронов. Более того, эти модели, в основе которых лежит движение электронов по некоторым разрешенным орбитам, противоречат нашим представлениям о необходимости вероятностного описания процессов в микромире атомно-молекулярных масштабов. Наша задача теперь – формализовать описание движения микрочастиц (в дальнейшем для определенности мы будем говорить об электронах) в пространстве, рассмотренное нами ранее на качественном уровне. Мы уже говорили о том, что частицу следует описывать с помощью некоторого волнового поля, причем это поле связано с вероятностью обнаружения микрообъекта в той или иной области пространства. В частности, частице с импульсом p (мы рассматриваем одномерный случай) соответствует волна
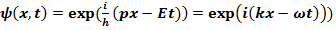 (17.1)
(17.1)
Попробуем теперь угадать волновое уравнение, решением которого является плоская волна (17.1), причем связь ω и k (дисперсионное соотношение) задается в виде:
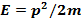 или
или 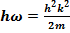 (17.2)
(17.2)
Дифференцируя один раз ψ(x,t) по времени и дважды – по пространственной координате, получим
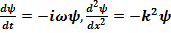 (17.3)
(17.3)
Сопоставляя теперь (17.3) с дисперсионным соотношением (17.2), мы понимаем, что искомое уравнение будет уравнением первого порядка по времени и - второго по пространственной координате. Действительно, умножая первое из соотношений (17.3) на
ih , получим
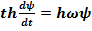 (17.4)
(17.4)
Аналогично, домножим второе из соотношений (6.3) на 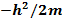 :
:
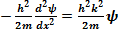 (17.5)
(17.5)
Сравнивая (17.4) и (17.5), получаем, что решение в виде плоской волны (17.1) с дисперсионным соотношением (17.2) удовлетворяет уравнению
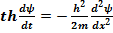 (17.6)
(17.6)
Уравнение (6.6) было получено Э. Шредингером в 1926 году, носит его имя и описывает движение частицы в свободном пространстве.
Обобщение на трехмерный случай делается элементарно. Выражение для волны
де Бройля запишем в виде
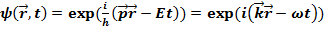 (17.7)
(17.7)
причем
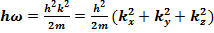 (17.8)
(17.8)
Здесь kx , ky , kz - проекции волнового вектора на соответствующие оси координат.
Тогда, очевидно, нестационарное уравнение Шредингера имеет вид
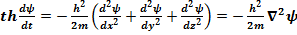 (17.9)
(17.9)
Обобщим это уравнение на случай движения частицы в потенциальном поле V ( 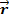 ,t) . Для
,t) . Для
этого вспомним, что в правой части уравнения (17.9) фактически стоит кинетическая
энергия частицы (см. выражение (17.2)). При наличии потенциального поля ее следует
заменить на полную энергию, т.е. добавить в (17.9) потенциальный член
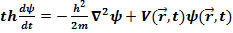 (17.10)
(17.10)
Уравнение (17.10) есть нестационарное уравнение Шредингера, описывающее движение
частицы в произвольном потенциальном поле.
Как видно, уравнение Шредингера (6.10) является уравнением первого порядка
по времени. Поэтому для его решения необходимо задать одно начальное условие, а именно, волновую функцию в некоторый начальный (например, нулевой) момент времени
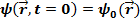 (17.11)
(17.11)
Тогда, зная волновую функцию системы в начальный момент времени, проинтегрировав
(17.10), мы сможем определить волновую функцию в любой наперед заданный момент
времени.
Нестационарное уравнение Шредингера есть основное уравнение квантовой механики и фактически приходит на смену классическим уравнениям Ньютона. Как мы уже отмечали, постановка задачи в классической механике (по начальным значениям
координаты и скорости (или импульса) определить значения этих величин в любой на-перед заданный момент времени) невозможна в квантовой теории. Соотношения неопределенностей Гейзенберга не позволяют в принципе задать начальные условия так, как это делается в классической теории. Состояние микрообъекта в квантовой теории описывается волновым полем, ψ - функцией. Вся информация, которую мы можем узнать о системе, содержится в ее волновой функции.
