Определение истинных значений удельного теплового потока, коэффициента теплопередачи, температур стенок и поверхности

Теплопередачи

3.6.1 Метод построения зависимости удельного теплового потока от температуры стенки

Наиболее наглядным методом определения истинных значений удельного теплового потока, коэффициента теплопередачи и температур стенок является графический метод построения нагрузочной характеристики проектируемого аппарата.

С этой целью задаются рядом значений температуры стенки со стороны горячего теплоносителя 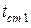в интервале от 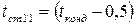до ,

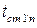где .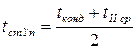

Затем для каждого значения температуры стенки по формулам (10-13) рассчитывают значения коэффициента теплоотдачи для конденсирующегося пара 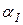и удельного теплового потока из уравнения теплоотдачи по формуле

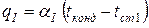. (27)

По полученному значению удельного теплового потока 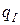, из уравнения теплопроводности

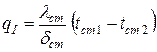(28)

определяют соответствующий ряд значений температуры стенки со стороны нагреваемой жидкости для чистых труб

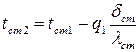, (29)

а для загрязненных труб по формуле

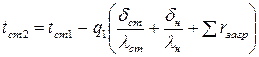, (30)

где 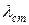– коэффициент теплопроводности материала трубок, Вт/м×К;

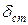– толщина стенки трубок, м;

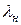– коэффициент теплопроводности накипи, Вт/м×К;

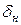– толщина слоя накипи, м;

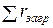– термическое сопротивление загрязнения, м²×К/Вт.

Для каждой температуры 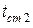с учетом режима движения жидкости по критериальным уравнениям рассчитывают коэффициент теплоотдачи для жидкости 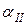по формулам (15,18,20-26) и удельный тепловой поток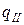

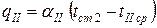
По результатам расчета строится график зависимости удельных тепловых потоков 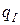и 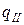от температуры стенки 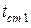, как показано на рисунке 8.

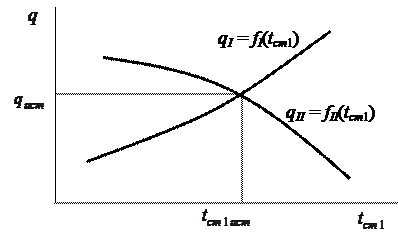
Рисунок 8 – Зависимость удельного теплового потока

от температуры стенки

Точка пересечения кривых 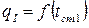и 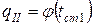дает истинное значение удельного теплового потока 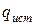и истинное значение температуры стенки 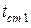, по которым из равенства

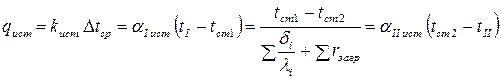
можно определить истинные значения коэффициентов теплоотдачи

,

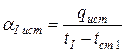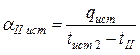
и температуры стенки

.

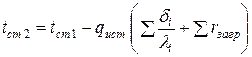3.6.2 Метод графического решения зависимости коэффициента
теплопередачи от удельного теплового потока

Для вертикального кожухотрубчатого теплообменника, применяя формулы для расчета коэффициентов теплоотдачи 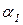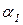(11) и 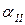(15,18,21-23,25,26), в зависимости от режима движения теплоносителя в трубном пространстве, выражают коэффициент теплопередачи 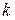, подставляя его в формулу удельного теплового потока (4)

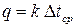
и получают уравнение 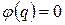, решая которое графически, находят истинное значение удельного теплового потока, показанного на рисунке 9.

Рисунок 9 – Графическое определение истинного

значения удельного теплового потока

Так, выражение для коэффициента теплопередачи в вертикальном кожухотрубчатом теплообменнике запишется в виде:

– для турбулентного режима движения теплоносителя:

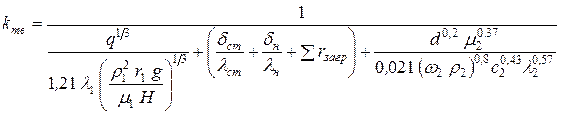, (31)

а уравнение 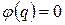в виде

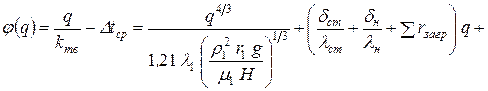
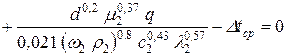; (32)

– для переходного режима:

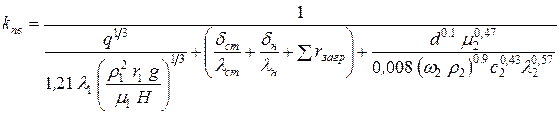, (33)

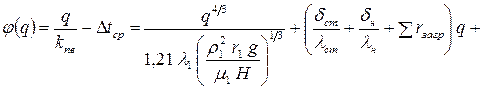
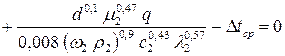; (34)

– для ламинарного режима:

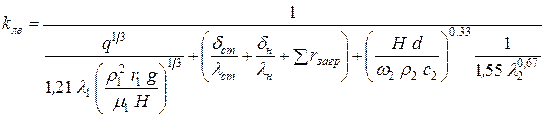, (35)

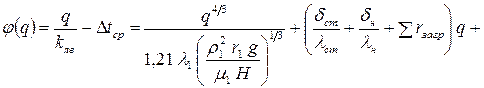
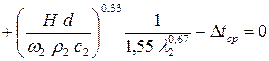. (36)

Аналогично, применяя формулы (13,15,18,21-23,25,26), получают выражения для коэффициента теплопередачи и уравнения 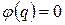для горизонтального кожухотрубчатого теплообменника:

– для турбулентного режима:

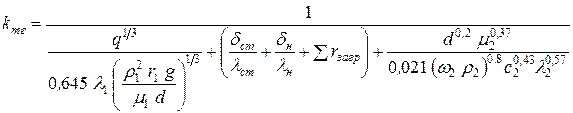, (37)

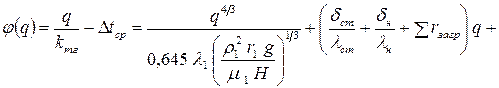
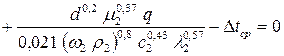; (38)

– для переходного режима:

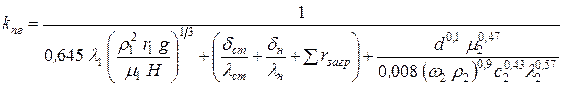, (39)

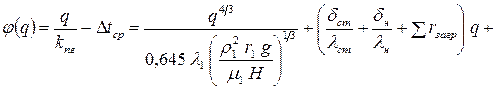
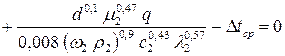; (40)

– для ламинарного режима:

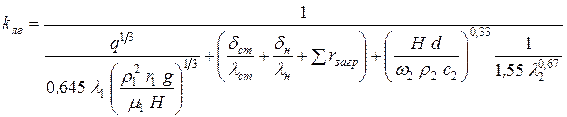, (41)

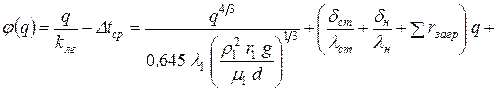
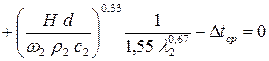. (42)

3.6.3 Расчет истинного значения коэффициента теплопередачи и поверхности теплообмена

По найденному истинному значению удельного теплового потока 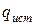рассчитывают истинное значение коэффициента теплопередачи

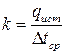
и поверхность теплообмена

.

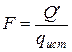3.7 Расчет истинных значений удельного теплового потока,
коэффициентов теплоотдачи и теплопередачи, температуры
стенок на ПК

Целью расчета является получение точных значений удельной тепловой нагрузки, коэффициентов теплоотдачи, теплопередачи и температуры стенок при заданной скорости движения раствора, а также исследование влияния скорости движения раствора на значение удельного теплового потока, коэффициентов теплоотдачи, теплопередачи для конкретного случая нагревания раствора «глухим» насыщенным паром в теплообменнике.

3.7.1 В программе приняты следующие обозначения:

А1	– коэффициент теплоотдачи от греющего пара к стенке, aI;
А2	– коэффициент теплоотдачи от стенки к раствору, aII;
Z	– коэффициент теплопередачи, k;
G1, G2	– удельный тепловой поток qI, qII;
Т1	– температура стенки со стороны греющего пара, tcm1;
Т2	– температура стенки со стороны раствора, tcm2;
Т3	– температура конденсации пара, tканд;
Т4	– средняя температура раствора, tII cр;
L1	– коэффициент теплопроводности конденсата греющего пара, λк;
Р1	– плотность конденсата, ρк;
М1	– динамический коэффициент вязкости конденсата, μк;
R	– удельная теплота конденсации греющего пара, r;
Р2	– плотность раствора, ρр;
С2	– удельная теплоемкость раствора, с;
L2	– коэффициент теплопроводности раствора, λр;
М2	– динамический коэффициент вязкости раствора, μр;
D	– наружный диаметр трубок, d;
В3	– толщина стенки трубок, δст;
L3	– коэффициент теплопроводности материала трубок, λст;
В4	– толщина слоя накипи, δн = 0,5 мм;
L4	– коэффициент теплопроводности накипи, λн;
О	– термическое сопротивление загрязнений стенок трубок, м2×К/Вт ;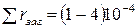
W2	– скорость движения раствора в трубках, w;
R2	– критерий Рейнольдса, Re.

Программа составлена для расчета теплообменников горизонтального типа.

Исходные данные, представленные в системе СИ, должны быть подготовлены на бланке, как показано в приложении А.

Для заполнения бланка необходимо из справочной литературы правильно выбрать физико-химические константы для конденсата греющего пара при рабочем давлении греющего пара и нагреваемого раствора.

3.7.2 Инструкция оператора

Зайти на диск М:\Dosapp\Upprog\MAXP\PAХТ\ТЕРLОLab_07.exe, cкопировать на диск D: файл Lab_07.exe, начать расчет.

3.7.3 Контрольный пример

3.7.3.1 Задание

Определить значения удельного теплового потока, коэффициентов теплоотдачи и теплопередачи, температуры стенок в горизонтальном трубчатом теплообменнике для нагревания раствора гидроксида натрия концентрацией 20 % «глухим» насыщенным водяным паром при заданной скорости движения раствора в трубах теплообменника при следующих условиях:

давление греющего пара – 0,202 МПа;

температура конденсации пара – 120 °С;

начальная температура раствора NaOH – 20 °С;

конечная температура раствора NaOH – 80 °С;

диаметр трубок – 38×3 мм;

материал трубок – Ст3, учесть наличие слоя накипи толщиной 0,5 мм загрязнение поверхности трубок – 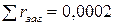м²×К/Вт.

Для исследования влияния скорости движения раствора в трубках на процесс теплопередачи выбирать предельное значение скорости 3 м/с.

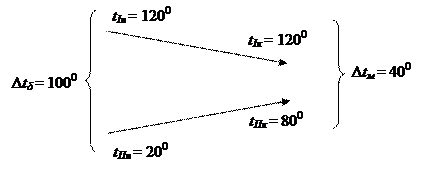
3.7.3.2 Определение среднего температурного напора

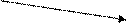Поскольку 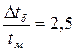> 2, для расчета применить формулу (7):

.

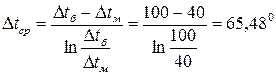3.7.3.3 Определение средней температуры нагреваемого раствора

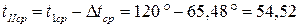°С.

3.7.3.4 Выбор физико-химических констант произвести для конденсата греющего пара при 120 °С, для нагреваемого раствора NaOH при 54,52 °С.

Исходные данные для расчета:

L1	– коэффициент теплопроводности конденсации греющего пара, λк = 0,686 Вт/(м2×К);
L2	– коэффициент теплопроводности раствора NaOH, λр = 0,557 Вт/(м2×К);
L3	– коэффициент теплопроводности стали, λст = 46,5 Вт/(м2×К);
L4	– коэффициент теплопроводности накипи, λн = 2,0 Вт/(м2×К);
М1	– динамический коэффициент вязкости конденсата, μк = 0,000231 Па×с;
М2	– динамический коэффициент вязкости раствора NaOH, μр = 0,00182 Па×с;
Н	– высота трубок, м
В3	– толщина стенки трубок, δст = 0,003 м;
В4	– толщина слоя накипи, δн = 0,0005 м;
R	– удельная теплота конденсации греющего пара, r = 2208000 Дж/кг;
О	– термическое сопротивление загрязнений стенок трубок, Srзагр = 0,0002 м2×К/Вт;
Р1	– плотность конденсата, ρк = 943 кг/м3;
Р2	– плотность раствора NaOH, ρр = 1198 кг/м3;
Т3	– температура конденсации пара, tконд = 120 °С;
Т4	– средняя температура раствора NaOH, tII cр = 54,52 °С;
D	– наружный диаметр трубок, d = 0,038 м;
С2	– удельная теплоемкость раствора NaOH, с = 3684 Дж/(кг×К);
W2	– скорость движения раствора NaOH в трубках, w = 1,5 м/с.

3.7.3.5 Результаты расчета удельного теплового потока, коэффициентов теплоотдачи и теплопередачи, температуры стенок при заданной скорости движения раствора NaOH приведены в приложении Б.