Зависимость скорости реакции от температуры

Скорость реакции с повышением температуры на 10 °C в большинстве случаев увеличивается в 2 – 4 раза (правило Вант-Гоффа). Поскольку концентрация реагентов изменяется в зависимости от температуры незначительно, то влияние последней сводится к изменению величины константы скорости. Для характеристики зависимости константы скорости от температуры был введен температурный коэффициент реакции:

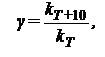(5.16)

где – константы скорости реакций при температурах T + 10 °C и T.

Если разность температур не равна десяти градусам, то равенство (5.16) запишется в виде

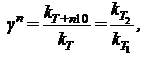Зная величину и константу скорости при температуре T₁, можно приблизительно вычислить константу скорости реакции при температуре T₂ по уравнению

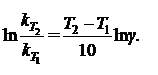(5.17)

Более точно зависимость константы скорости от температуры выражается уравнением Аррениуса:

а) в дифференциальной форме

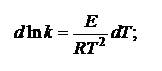(5.18)

б) в интегральной форме

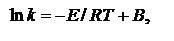(5.19)

или

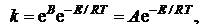(5.20)

где E – энергия активации; B – постоянная интегрирования; A = e^B.

Энергия активации – это та минимальная избыточная энергия (по сравнению со средней энергией молекул), обладая которой, молекула вступает в химическую реакцию. Так как не любое столкновение молекул ведет к образованию новой молекулы, т. е. к протеканию химической реакции, химическое взаимодействие происходит только между активными молекулами, обладающими энергией, равной или большей энергии активации E.

Для элементарных реакций значения E и A мало зависят от температуры и в небольшом температурном интервале их можно считать постоянными.

Определение опытной энергии активации возможно провести следующим образом: решение уравнения Аррениуса (5.19) для двух температур имеет вид

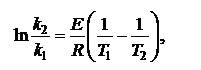или

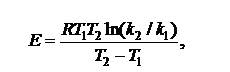(5.21)

где k₁ и k₂ – константы скорости реакции при температурах T₁ и T₂.

Следовательно, для расчета энергии активации по уравнению (5.21) следует экспериментально определить константу скорости реакции при двух температурах.

Для более точного определения значения энергии активации необходимо иметь данные о константах скорости при четырех и более температурах. В этом случае энергия активации вычисляется графически.

Если для изучаемой реакции уравнение Аррениуса применимо, то в соответствии с равенством (5.19) ln k должен линейно зависеть от обратной температуры, т. е. если отложить опытные значения k от температуры в координатах ln k = f (1/T), то все точки должны находиться на одной прямой (рис. 5.3). Энергия активации будет равна E = – R tg α.

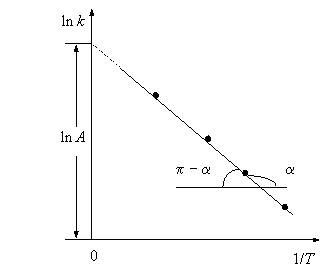
Рис. 5.3. Зависимость логарифма константы скорости реакции от обратной температуры