Вытекание газа из отверстия сосуда в вакуум

Найдем число частиц, выходящих из отверстия сосуда с газом в вакуум. Размер отверстия должен быть достаточно малым, чтобы вытекающий поток был слабым, распределение частиц в газе оставалось равновесным, и можно было использовать полученные ранее функции распределения.

Направляем ось z перпендикулярно плоскости отверстия площадью S. Используем распределение (2.43) в сферических координатах

.

Осевая симметрия системы позволяет проинтегрировать распределение по углу j

– концентрация частиц газа, движущихся с модулем скорости под углом .

Число вылетающих за 1с частиц под углом q со скоростью v пропорционально эффективной площади отверстия в направлении движения

,

скорости частиц и концентрации

,

тогда

(П.5.7)

– число частиц, вылетающих за 1с через отверстие площадью S с модулем скорости под углом .

Интегрируем (П.5.7) по модулю скорости v в интервале (0, ¥) используя

,

, , ,

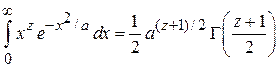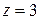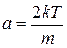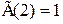и находим число частиц, вылетающих за 1с со всеми скоростями под углом :

, (П.5.8)

где плотность потока частиц (2.52)

.

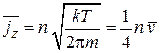Согласно (П.5.8) число частиц, вылетающих в единичный интервал угла около значения q:

.

Пунктирная линия на рисунке является функцией распределения по углу. При распределение зануляется из-за обращения в нуль телесного угла , через который идет поток частиц. Максимум распределения находится при q = 45°.

Интегрируем (П.5.7)

по углу q в интервале (0, p/2). Используем

,

и находим число частиц, вылетающих за 1с по всем направлениям со скоростями в интервале :

. (П.5.9)

Интегрируя (П.5.8) по углу, или (П.5.9) по скорости, и получаем число частиц, вылетающих через отверстие за секунду со всеми скоростями и под всеми углами

. (П.5.10)

Результат очевиден, поскольку 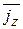– число частиц, движущихся со скоростями , и произвольными , , и пересекающих единичную поперечную оси z площадку за одну секунду.

Полученные формулы не учитывают рассеяния частицы при прохождении отверстия. Это предположение выполняется для малого отверстия, когда его размер гораздо меньше длины свободного пробега частицы.

Термоэлектронная эмиссия

Качественное описание. У элементов первой группы таблицы Менделеева (Li, Na, K, Cu, Rb, Ag, Cs, Au) валентный электрон слабо связан с ядром. При объединении атомов в кристалл валентные электроны отсоединяются от атомов и становятся свободными. Решетка положительных ионов экранирует заряд электрона на расстояниях порядка периода решетки. В результате электроны не оказывают силового воздействия друг на друга и образуют идеальный газ. Их концентрация пропорциональна концентрации узлов решетки . При средняя энергия электрона

,

он движется со скоростью ~ 100 км/с. Такой кристалл проявляет металлические свойства.

На границе металл–вакуум существует двойной электрический слой, препятствующий выходу электронов из металла. Внешний слой – облако электронов, кратковременно выходящих и возвращающихся назад под действием положительных ионов. Внутренний слой – положительные ионы, не скомпенсированные вышедшими электронами.

Объем металла для электрона оказывается потенциальной ямой с работой выхода

А @ 5 эВ.

Поскольку , то из металла выходит малая часть электронов, соответствующих хвосту распределения Максвелла. Вероятность выхода электрона из металла равна заштрихованной площади на рисунке распределения плотности вероятности по энергии.

Количественное описание. Минимальную скорость , необходимую для выхода, находим из закона сохранения энергии

,

.

По аналогии с плотностью потока частиц (2.51) вдоль оси z, перпендикулярной поверхности металла

,

где согласно (2.42а)

,

находим плотность потока электронов, выходящих из металла:

.

Интеграл вычисляем заменой аргумента

, ,

,

тогда

, (П.5.12)

где

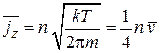
– плотность потока электронов, движущихся из объема металла к поверхности;

– вероятность выхода электрона из металла. Плотность электрического тока термоэмиссии

(П.5.13)

– формула Ричардсона (1901 г.). Нобелевская премия по физике 1928 г.

Сэр Оуэн Вильямс Ричардсон (1879–1959)