Условия стандартного состояния веществ
Законы термохимии
Термохимические уравнения - химические уравнения реакций, в которых указаны агрегатные состояния веществ и тепловые эффекты
Например, Н2(г) + 1/2О2(г) = Н2О(ж); ΔrНо298 = -285,84 кДж
Qp = H2 – H1 = Dr H ΔrН<0 - экзотермическая реакция (Q выделяется)
ΔrН>0 - эндотермическая реакция (Q поглощается)
Для газофазной реакции рассчитывается молекулярное уравнение, а для реакций в растворах – ионно-молекулярное уравнение.
Задача 2
Записать термохимические уравнения а) для газофазной реакции получения аммиака и б) реакции нейтрализации сильной кислоты сильным основанием, протекающей в растворе.
Решение
а) Для газофазной реакции записывается молекулярное уравнение:
3/2 Н2(г) +1/2N2(г) ↔ NH3(г) ΔrНо298 = -46,19 кДж
б) Для реакции, протекающей в растворе записывается ионно-молекулярное уравнение
Н+(р-р) + ОН-(р-р)→ Н2О(ж) ΔrНо298 = -55,9 кДж
(для реакции нейтрализации любой сильной кислоты любым сильным основанием тепловой эффект равен -55,9 кДж/моль Н2О(ж) )
1. Закон Ломоносова, Лавуазье-Лапласа Qобр.i = - Qразл.i
2. Закон Гесса Тепловой эффект реакции не зависит от пути ее протекания, а зависит лишь от природы и состояния исходных веществ и продуктов
А 1 В


2 3 DrНт (1) = DrНт (2) + DrНт(3)
С
Следствие из закона Гесса: энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов ν
Так, для веществ в стандартных состояниях:
ΔrН0 = ∑νiΔfНi0 продуктов - ∑νjΔfНj 0исх веществ
Условия стандартного состояния веществ
| Состояние вещества | Стандартное состояние вещества: устойчивое состояние при Т=const и Р = 105 Па |
| Простое твердое вещество | Кристаллическое твердое вещество |
| Простое жидкое вещество | Чистая жидкость |
| Газообразное | Парциальное давление Р=100 кПа (1атм) или относительное давление 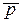 = 1 ( = 1 ( 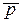 = р, Па/105Па) = р, Па/105Па) |
 Растворенное Растворенное | Концентрация 1 моль/л |
Энтальпия (теплота) образования веществаDfН -тепловой эффект реакции образования 1 моль сложного вещества из простых веществ, устойчивых при 298 К и давлении 100 кПа
Cтандартная энтальпия (теплота) образования веществаDfН0 -тепловой эффект реакции образования 1 моль вещества в стандартном состоянии из простых веществ, находящихся в стандартном состоянии.
DfН0298 - табличные данные – при 298 К.
ΔfН0298 = 0 для простых веществ (О2-газ, Br2-жидкость, Р-белый , Snбелое , S(к)ромб ….)
Задача 3
Написать термохимическое уравнение реакции, тепловой эффект которой равен энтальпии образованияH2SO4(ж)
Решение
H2(г)+2O2(г)+S(к)=H2SO4(ж), DrН°298 = -811,3 кДж/моль
DrН°298 = ΔfН0298H2SO4(ж) - ΔfН0298H2(г) - 2ΔfН0298O2(г) - ΔfН0298S(к) = -811,3 -0-2.0-0 =-811,3 кДж/моль (табличные данные)
Задача 4
Определить ∆rH0298 реакции С(к) + СО2(г) = 2СО(г) (1), если известно
(2) 2С(к) + О2(г) = 2СО(г) , ∆rH0298 (2) = -221 кДж
(3) 2СО(г) + О2(г) = 2СО2(г) , ∆rH0298 (3)= -566,1 кДж
Решение
К термохимическим уравнениям можно применять любые алгебраические действия: ур.1 = ½ ур.2 – ½ ур.3
½(2С(к)+О2(г) - 2СО(г) - О2(г)) = ½×(2СО(г) - 2СО2 (г)) После преобразования получим С(к) + СО2(г) = 2СО(г)
∆rH01= ½ (∆rH02-∆rH03) = ½[-221–(-566,1)]= 172,5 кДж
Теплота сгорания топлива ∆H0сг – тепловой эффект реакции окисления молекулярным кислородом элементов, входящих в состав этого топлива до образования высших оксидов.
Удельная теплота сгорания Qт - количество теплоты, выделяющейся при сгорании жидкого или твердого топлива массой 1 кг и газообразного вещества объемом 1 м3 до образования высших оксидов. Если расчет Qт ведется применительно к реакции с образованием H2O(ж), то Qт называется высшей, а для реакции с образованием H2O(г) называется низшей. По умолчанию обычно имеют в виду Qт высшую.
Для жидкого или твердого вещества Qт = -∆H0cг1000/M, кДж/кг (М, г/моль – молярная масса вещества)
Для газообразного вещества Qт = -∆H0cг1000/Vm, кДж/м3 (Vm =22,4, л/моль – молярный объем газа при н.у Т=273К и Р=101,3 кПа).
Задача 5
Определить удельную теплоту сгорания ∆H0сг (кДж/м3) газовой смеси объемного состава: этилен C2H4(Г) - 20% и пропан 80%
Решение
Уравнения реакций:
C2H4(Г) + 3 O2 (г) = 2 CO2(г) + 2 H2O(ж) DrН°298 = H0cг C2H4(Г) = -1312,00кДж/моль
C3H8(г) + 5 O2 (г) = 3 CO2(г) + 4 H2O(ж) DrН°298 = ∆H0cг C3H8(г) = -2436,26 кДж /моль
Расчет DrН°298 = H0cг по следствию из закона Гесса:
∆H0cгC2H4(Г) =2 ∆fH0CO2(Г) +2∆fH0H2O(Ж) - ∆fH0C2H4(Г)- 3 ∆fH0O2(г) = 2(-396,3)+ 2(-285,84) –52,28 – 0 = -1312,00 кДж.
∆H0cгC3H8(г) =3 ∆fH0CO2(г) +4 ∆fH0H2O(ж) -∆fH0C3H8(г)- 5 ∆fH0O2 (г) = 3(-396,3) + 4(-285,84) –(-104) – 0 = -2436,26 кДж.
Удельная теплота сгорания:
Qт C2H4(Г) = -∆H0cг1000/Vm = 1312,00.1000/22,4 = 58571, 4 кДж/м3 при н.у
Qт C3H8(г) = -∆H0cг1000/Vm = 2436,26.1000/22,4 = 108761,6 кДж/м3 при н.у
Удельная теплота сгорания газовой смеси объемного состава: этилен C2H4(Г) - 20% и пропан 80%:
Qт = 0,2 Qт C2H4(Г) + 0,8 Qт C3H8(г) = 0,2. 58571, 4 + 0,8. 108761,6 = 98723,56 кДж/м3 при н.у.
Задача 6
Определить удельную теплоту сгорания ∆H0сг (кДж/м3) жидкого топлива – пентана
Решение
Уравнение реакции сгорания топлива :
C5H12(ж) + 8 O2 (г) = 5 CO2(г) + 6 H2O(ж) DrН°298 = ∆H0cг C5H12(ж) = -3590,28Дж/моль.
Расчет DrН°298 = H0cг - стандартной теплоты сгорания C5H12(ж) по следствию из закона Гесса:
∆H0cгC5H12(ж)=5∆fH0CO2(Г)+6∆fH0H2O(Ж)-∆fH0С5H12(ж)-8∆fH0O2(г) =(-396,3)+6(-285,84)–(-10б,26)–0=-3590,28Дж/моль.
Молярная масса пентана C5H12 МC5H12 = 72 г/моль.
Удельная теплота сгорания жидкого топлива:
Qт=-∆H0cгC5H12(ж)1000/MC5H12=-(-3590,28)∙1000/72=44879 кДж/кг=44,878 мДж/кг.
.
Задача 7
Определить удельную теплоту сгорания ∆H0сг (кДж/м3) жидкого топлива – пентана, содержащего 10 % негорючих примесей.
Решение
Уравнение реакции сгорания топлива :
C5H12(ж) + 8 O2 (г) = 5 CO2(г) + 6 H2O(ж) DrН°298 = ∆H0cг C5H12(ж) = -3590,28Дж/моль.
Расчет DrН°298 = H0cг - стандартной теплоты сгорания C5H12(ж) по следствию из закона Гесса:
∆H0cгC5H12(ж)=5∆fH0CO2(Г)+6∆fH0H2O(Ж)-∆fH0С5H12(ж)-8∆fH0O2(г) =(-396,3)+6(-285,84)–(-10б,26)–0=-3590,28Дж/моль.
Молярная масса пентана C5H12 МC5H12 = 72 г/моль..
Удельная теплота сгорания при содержании в топливе 10 % об. негорючих примесей.
Qт = -∆H0cгC5H12(ж)1000∙(1-0,1)/MC5H12= -(-3590,28)∙1000/72=44879 кДж/кг=44,878 мДж/кг,
где0,1 – доля (об.) негорючих примесей в топливе.
Задача 8
Определить массу жидкого топлива - пентана, которое сожгли, если при полном его сгорании выделилось 448 л (н.у.) диоксида углерода CO2. Сколько тепла при этом получили? Напишите уравнение реакции. ∆H0cг C5H12(ж) = -3590,28Дж/моль.
Решение
Уравнение реакции сгорания топлива:
C5H12(ж) + 8 O2 (г) = 5 CO2(г) + 6 H2O(ж) DrН°298 = ∆H0cг C5H12(ж) = -3590,28Дж/моль.
МC5H12 = 72 г/моль 5∙22,4 л
C5H12(ж) + 8 O2 (г) = 5 CO2(г) + 6 H2O(ж) ∆H0cг C5H12(ж) = - 3590,28 кДж/моль
M г 448 л
Составим пропорцию:
по стехиометрии реакции при сжигании топлива C5H12(ж) :
1 моль (М=72 г/моль) C5H12(ж) - выделяется 5Vm=112 л(н.у) CO2(г) и -∆H0cг C5H12(ж) = 3590,28 кДж/моль
n моль (m C5H12(ж), г) C5H12(ж) - выделяется V CO2= 448 л(н.у) CO2(г) и Q кДж тепла
Сожгли m C5H12(ж) = VCO2∙ МC5H12/5Vm = 448 ∙ 72/112 = 288 г C5H12(ж)
или n C5H12(ж) = VCO2 /5Vm = 448 /112 = 4 моль C5H12(ж).
Получили Q = -∆H0cгC5H12(ж) ∙ n C5H12(ж) = -(-3590,28)кДж/моль ∙ 4 моль = 14361 кДж = 14,361 мДж тепла.
Задача 9
Вычислить количество тепла, выделяющееся при сгорании 100 м3 этилена C2H4(Г) (условия нормальные). Написать уравнение процесса горения
Решение:
Дано: V C2H4(г) = 100 м3 (н.у.)
Определить Q
Уравнение реакции:
C2H4(г) + 3 O2 (г) = 2 CO2(г) + 2 H2O(ж) ∆H0cг C2H4(Г) = -1312,00кДж/моль
.
По следствию из закона Гесса:
∆H0cгC2H4(Г)=2∆fH0CO2 (Г) +2∆fH0H2O(Ж) - ∆fH0C2H4(Г)- 3∆fH0O2 (г) =2(-396,3)+2(-285,84) –52,28 – 0 = -1312,00 кДж
Vm=22,4 л/моль (н.у) – мольный объем любого газа при нормальных условиях.
По уравнению реакции при сжигании топлива C2H4(Г
Vm=22,4 л/моль (н.у) C2H4(Г) (1 моль) - выделяется (-∆H0cг C2H4(Г))=1312,00кДж/моль тепла
V = 100 м3 (н.у.) C2H4(Г) - выделяется Q кДж тепла____________________
Q =-∆H0cг (C2H4(Г) ∙V C2H4(г)∙1000/ Vm= - (-1312,00)кДж/моль∙(100∙1000)л /22,4 л/моль = 5857∙103 кДж = 5857 МДж тепла
Зависимость ΔrН0 от температуры:
В интегральном виде для области температур (298÷Т) К, уравнение Кирхгофа:
∆rH0T = ∆rH0298 + 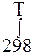 ∆rС0pdT
∆rС0pdT
Сpо –теплоемкость вещества, функция состояния системы
∆rСpо -изменение стандартной теплоемкости системы в ходе реакции
∆rСpо =∑νi Срi0 прод -∑νj Срj 0исх веществ
В отсутствие фазовых переходов веществ:
1-приближение:Ср ¹ ¦(Т) (Ср,i =соnst), тогда ∆rС0р= соnst ∆rН0Т = ∆rН0298 + ∆rС0р(Т - 298)
2 – приближение:при Т ~ 298 К ∆rС0р,i = 0 ∆rH0T = ∆rH0298
3 – есть фазовый переход в области температур (298 ÷ Т) К
∆rН0Т = ∆rН0298 + ∆rС0р(1)(Тфп - 298) +∆rН0фп + ∆rС0р(2)(Т - Тфп)
2–ой закон термодинамики:в изолированных системах энтропия самопроизвольно протекающего процесса возрастает, т.е. ∆S > 0.
S - энтропия мера неупорядоченности состояния системы. Чем больше порядок, тем меньше S . S – функция состояния системы
Неупорядоченность системыопределяется еемакросостоянием,определяемым либо параметрами (P, T…), либо через громадное число микросостояний составляющих ее частиц, т.е. их мгновенными координатами и скоростями различных видов движения частиц в различных направлениях. Число микросостояний системы, с помощью которых может быть охарактеризовано ее макросостояние, называюттермодинамической вероятностью W: S = k lnW, Дж/(моль·К)
k –постоянная Больцмана k = R/Nа =1.38×10-23 Дж/К
3–ой закон термодинамики(М. Планк): при абсолютном нуле энтропия идеального кристалла равна нулю (полная упорядоченность) W=1, S = k ln1 = 0
S вещества растет с увеличением температуры и скачкообразно возрастает в точках фазовых переходов
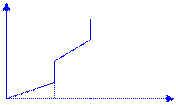 S, Дж/(моль·К)
S, Дж/(моль·К)
газы – носители S
Тпл Ткип Т, К
Для любой Т можно определить абсолютное значение S чистого вещества.
Cтандартная энтропия S0, Дж/(моль×К) - энтропия вещества, находящегося в стандартном состоянии. S0298 - справочные данные.
Задача 10
Дайте качественную оценку изменения энтропии реакций: а) Ст + СО2,г ® 2СОг DrS0= 87 Дж/К; б) 3Н2,г+ N2,г ® 2NH3,г DrS0= -90 Дж/К; в) Ст + О2,г ® СО2г; DrS0=2,9 Дж/К.
Решение
а) Ст + СО2,г ® 2СОг DrS0= 87 Дж/К > 0 – неупорядоченность системы увеличивается за счет увеличения объема системы (изменение числа молей газов ∆nгаз = 2-1=1>0);
б) 3Н2,г+ N2,г ® 2NH3,г DrS0= -90 Дж/К< 0 - неупорядоченность системы уменьшается за счет уменьшения объема системы (∆nгаз = 2-3-1=-2<0);;
в) Ст + О2,г ® СО2г; DrS0=2,9 Дж/К@0 объем системы практически не изменяется (∆nгаз = 1-1=0), но DrS0>0 за счет усложнения молекул: из двух простых веществ – Ст и О2 газ образуется газообразное сложное вещество СО2 газ.
Изменение энтропии системыпри теплообмене с окружающей средой ΔS = Q/T; при фазовом переходе ΔSфп= ∆Hфп/Tфп. Изменение энтропии химической реакции:ΔrS = ∑νi Si продуктов - ∑νj Sj исх веществ
Для стандартных состояний веществ и Т=298 К: ΔrS0298 = ∑νiS0298,i продуктов - ∑νjS0298,j исх веществ
ΔrS0298 – стандартная энтропия реакции при 298К
Зависимость ΔrS от температуры:
в области ( 298 ÷Т)нет фазовых переходов: ∆rS0T = ∆rS0298 + 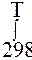
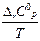 dT
dT
1 приближение: Ср ¹ ¦(Т) (Ср,i = соnst), тогда ∆rС0р= соnst и ∆rS0T = ∆rS0298 + ∆rС0р ln 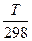
2 приближение: при Т ~ 298 К ∆rС0р,i = 0и ∆rS0T = ∆rS0298
3 - в области (298 ÷ Т) К есть фазовый переход. Для приближенных расчетов:
∆rS0Т = ∆rS0298 + ∆rС0р(1)( lnТфп - ln298) +∆rS0фп + ∆rС 0р(2)( lnТ - lnТфп)
Зависимость S реакции от Р особенно заметна в случае газовых реакций:∆Si =Sрi – S0i = - R ln(p/p0)изменение энтропии 1 моля газа при увеличении давления от 1 атм до р:∆Si = - R ln 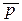 i
i
Задача 11
Определите ∆rH0298, ∆rH01000, ∆rS0298 и ∆rS01000 реакции С(к) + СО2(г) = 2СО(г), считая постоянными теплоемкости реагентов в данном температурном интервале.
Решение. ∆rН0Т = ∆rН0298 + ∆rС0р(Т - 298) ∆rS0T = ∆rS0298 + ∆rС0р ln 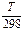
Табличные данные:
| Вещество | ΔfН0298,кДж/моль | S0298,Дж/(моль.K) | С0р298 ,Дж/моль.К |
| С(графит) | 0,0 | 5,74 | 8,54 |
| СО2 (г) | -393,5 | 213,68 | 37,41 |
| СО (г) | -110,5 | 197,54 | 29,14 |
По следствию из закона Гесса ΔrН0298 =∑νiΔfНi0 продуктов -∑νjΔfНj 0исх веществ =ΔfН0298 СОг -ΔfН0298 Ск -ΔfН0298 СО2г = 2(-110,5) – 0 – (-393,5) = 172,5 кДж > 0 - реакция эндотермическая
Т.к. Ср – функция состояния, то ∆rС0р = ∑νiСр i0 продуктов - ∑νjСр j 0исх веществ = 2С0р298СОг–С0р298Ск–С0р298СО2г= 2.(29,14)–8,54–37,41 =12,33 Дж/К.
∆rН01000 =172,5 + 12,33.10-3.(1000 - 298) = 181,16 кДж.
│(∆rН0298 - ΔrН01000)│100% /│ΔrН0298│ = │(172,5 - 181,16)│100% /172,5 = 5%.
Так как S – функции состояния, то ΔrS0298 =∑νiS0298,i прод. - ∑νjS0298,j исх веществ =2S0298,СОг - S0298,Ск - S0298,СО2г = 2(197,54)–5,74–213,68=175,66 Дж/K>0 – неупорядоченность системы повышается т.к. реакция протекает с увеличением числа молей газов (Δnгаз = 2-1=1>0).
∆rS01000 =∆rS0298 + ∆rС0рln 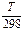 =175,66+12,33ln(1000/298)=175,66+14,93=190,59 Дж/К. При DT = 702К
=175,66+12,33ln(1000/298)=175,66+14,93=190,59 Дж/К. При DT = 702К
│(∆rS0298 - ΔrS01000) │100% /│ΔrS0298│ = │ (175,66 - 190,59 │100% /175,66 @ 8,5%.
При изменении температуры на 702 К увеличение теплового эффекта составляет 5%, а энтропии – 8,5%.
| Направление химических процессов. Энергия Гиббса. Энергия Гельмгольца Направление процесса определяется соотношениемэнтальпийного ∆rН (стремление системы к упорядоченности) иэнтропийного Т∙∆rS (стремление системы к хаотичности) факторов реакции. Функцией состояния системы,учитывающей совместное влияние ∆rН и Т∙∆rS на самопроизвольное протекание реакции, является свободная энергия: -при P, Т = const это энергия Гиббса или изобарно-изотермический потенциал ∆rGТ=∆rНТ - Т∙∆rSТ - при V, Т = const это энергия Гельмгольца или изохорно-изотермический потенциал ∆rFТ=∆rUТ - Т∙∆rSТ Критерий термодинамической возможности самопроизвольного протекания реакции в прямом направлении: · в изобарно-изотермических условиях: ∆rGТ < 0 · в изохорно-изотермических условиях: ∆rFТ <0 Соотношение между ∆rGТ и ∆rFТ: ∆rGТ - ∆rFТ = ∆n·RT Aпол = - DG «свободная энергия»,та часть теплового эффекта, которую можно превратить в работу. Т ΔS «связанная энергия»,та часть теплового эффекта, которая рассеивается в окружающую среду DrG < 0Самопроизвольный процесс - реакция в прямом направлении DrG > 0Реакция в обратном направлении DrG = 0Реакцияв равновесномсостоянии |
| знак | Принципиальная возможность и условия протекания прямой реакции | ||||||||
| ∆rН | ∆rS | DrG | |||||||
| - | + | - | Возможна при любой температуре | ||||||
| + | - | + | Невозможна. Возможна в обратном направлении | ||||||
| - | - | - | Возможна при низких температурах 298 < Т< Тр | ||||||
| + | + | - | Возможна при высоких температурах Тр< Т< Тсущ | ||||||
DrG рассчитывают двумя способами:
· 1 способ При Т=298К ΔrG0298 = ∑νiΔfG0298,i продуктов - ∑νjΔfG0298,j исх веществ
Энергия Гиббса образования вещества ∆fG –энергия Гиббса реакции образования 1 моль сложного вещества из простых веществ, устойчивых в данных условиях
∆fG0- стандартная энергия Гиббса образования вещества(вещества находятся в стандартном состоянии) ∆fG0298, -табулирована [кДж/моль] ∆fG0298 (простых веществ)= 0
· 2 способ ΔrGT = ∆rHT - T∆rST (зависимости ∆rH и ∆rS от Т – см. выше)
ΔrG0298 = ∆rH0298 - T∆rS0298
Когда ∆rС0р,i = 0: ΔrG0Т = ∆rH0298 - T∆rS0298
Задача 12
Рассчитать ∆rH0298 , ∆rS0298 , ∆rG0298 (двумя способами) реакции С(к) + СО2(г) = 2СО(г) и сделать вывод о возможности самопроизвольного протекания реакции при стандартных состояниях веществ и 298 К.
Решение:Табличные данные:
| Вещество | ΔfН0298, кДж/моль | S0298, кДж/(моль.K) | ∆fG0298, кДж/моль |
| С(графит) | 0,0 | 5,74 | 0,0 |
| СО2 (г) | -393,5 | 213,68 | -394,4 |
| СО (г) | -110,5 | 197,54 | -137,14 |
Следствие из закона Гесса:энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов ν
Так, для веществ в стандартных состояниях при Т=298 К (табличная Т)
ΔrН0298=∑νiΔfНi0298 продуктов -∑νjΔfНj 0 298 исх веществ=2ΔfН0298 СО(г)- ΔfН0298 С(к) - ΔfН0298 СО2(г)=2(-110,5)–0 –(-393,5) = 172,5 кДж. ΔrН0298 >0 - реакция эндотермическая
S и G – функции состояния и для них:
ΔrS0298 =∑νiS0298,i продуктов-∑νjS0298,j исх веществ=2S0298СО(г)-S0298 С(к)- S0298 СО2(г)= 2(197,54)–5,74–213,68=175,66 Дж/K ΔrS0298>0 - реакция протекает с увеличением числа молей газообразных веществ ∆νгаз = 2 – 1 = 1>0
ΔrG0298 = ∑νiΔfG0298,i продуктов - ∑νjΔfG0298,j исх веществ = 2Δf G0298 СО(г) - Δf G0298 С(к) - Δf G0298 СО2(г) =2(-137,14) – 0 – (-394,4) = 120.09 кДж
2 способ: при Т=298 К ∆rG0298 = ∆rH0298 - T∆rS0298= 172,5 – 298.175,66.10-3 = 120,15 кДж
Значения ∆rG0298, рассчитанные двумя способами практически совпадают.
Критерий термодинамической возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях – уменьшение энергии Гиббса системы: ∆rGТ < 0
Т.к. ∆rG0298 > 0 – самопроизвольное протекание реакции при стандартных состояниях всех участников и Т=298 К в прямом направлении невозможно, реакция будет протекать в обратном направлении.
Задача 13
Определить температурную область самопроизвольного протекания реакции С(к)+ СО2(г) = 2СО(г) при стандартных состояниях компонентов (ΔrН0298 =172,5 кДж, ∆r S0298 =.175,66 Дж/К)
Решение
| Вещество | Интервал температур, .К |
| С(графит) | (298 – 2300) К |
| СО2 (г) | (298 – 2500) К |
| СО (г) | (298 – 2500) К |
Тсущ. = 2300 К (для наименее устойчивого вещества - графита)
∆rGТ=∆rНТ - Т∙∆rSТ -энергия Гиббса или изобарно-изотермический потенциал, это функция состояния системы, учитывающая совместное влияние энтальпийного (∆rН) и энтропийного (Т∙∆rS) на самопроизвольное протекание реакции при P, Т = const (свободная энергия).
Реакция протекает самопроизвольно при стандартных состояниях компонентов, если ∆rG0Т = ∆rH0298 - T∆rS0298 < 0. С учетом приближения 2: ∆rH0Т = ∆rH0298 и ∆rS0Т = ∆rS0298 (энтальпия и энтропия реакции не зависят от температуры), график зависимости ∆rG0Т (Т) линейный.
При температуре равновесия Тр = ∆rH0298 /∆rS0298 = 172,5/175,66.10-3 = 928 K – равновероятно протекание как прямой, так и обратной реакции т.к. при этой температуре ∆rG0Т = 0.
Энтальпийный фактор (стремление системы к упорядоченности) ΔrН0298 =172,5 кДж >0 не способствует протеканию реакции при низких температурах, а энтропийный фактор (стремление системы к хаотичности) Т∙∆r S0298 = Т.175,66 Дж >0 определяет отрицательный знак энергии Гиббса при высоких температурах. Сл.самопроизвольное протекание процесса при стандартных состояниях возможно при Т>Тр.
Область температур, в которой возможно самопроизвольное протекание реакции при стандартных состояниях веществ (∆rG0Т<0):
∆rG0Т , кДж
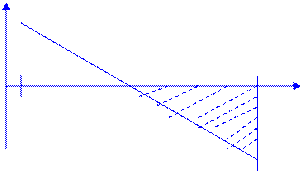 Тр= 982 К < Т < 2300К = Тсущ..
Тр= 982 К < Т < 2300К = Тсущ..
∆rG0298 = 120,09
∆rG0Т = ∆rH0298 - T∆rS0298
ТрТсущ
298 982 2300 Т, К
∆rG0Т<0
Зависимость ΔrGT от давления - изотерма Вант Гоффа:
Для реакции: aAг + bBг + dDк = eEг + fFг  ΔrGТ =∆rG0Т + RTln
ΔrGТ =∆rG0Т + RTln 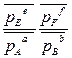
где 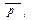 – относительные парциальные давления газообразных веществ.
– относительные парциальные давления газообразных веществ.
Для реакции:aA(р)+bB(р)+dD(к) = eE(р)+fF(р) протекающей в идеальном растворе (∆V = 0) ∆rGºT=∆rFºT= - RTln (ceE равн cfF равн / caA равн cbB равн)
Задача 14
При каком соотношении парциальных давлений газообразных компонентов реакции С(к)+СО2(г)=2СО(г) возможно ее протекание в прямом направлении при 298К (∆rG0298 = 120,15 кДж)?
Решение
Возможность самопроизвольного протекания реакции определяется ∆rG298< 0
По уравнению изотермы Вант-Гоффа: ΔrG298=∆rG0298+RTln 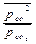 < 0.
< 0.
Пусть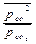 = х, тогда 120,15+8,31.10-3.298 lnх<0, отсюда lnх<-48,5 Þ х=
= х, тогда 120,15+8,31.10-3.298 lnх<0, отсюда lnх<-48,5 Þ х= 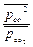 <10-21 или
<10-21 или 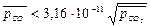
Задача 15
Определите, изменится ли направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10 Па для реакции С(к)+СО2(г)=2СО(г) при Т = 1000 К (ΔrН0298 =172,5 кДж, ∆r S0298 =.175,66 Дж/К)
Решение
Зависимость ΔrGT от давления выражается изотермой Вант Гоффа (С(к)- вещество в кристаллическом состоянии не входит в 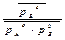 ):
):
ΔrGТ = ∆rG0Т + RTln 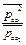 при Т=1000 К ΔrG1000 = ∆rG01000 + RTln
при Т=1000 К ΔrG1000 = ∆rG01000 + RTln 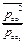
Энергия Гиббса реакции при стандартных состояниях веществ, т. е. относительных парциальных давлениях СО2 и СО равных 1: ΔrG0Т = ∆rH0298 - T∆rS0298 (считая ∆rС0р = 0, т.е. ∆rH0Т = ∆rH0298 и ∆rS0Т = ∆rS0298 - энтальпия и энтропия реакции не зависят от температуры)
при Т=1000К ΔrG01000 =172,5- 1000∙175,66.10-3 = -3,16 кДж ˂ 0 – возможно самопроизвольное протекание реакции при стандартных состояниях и Т=1000К
Для заданных начальных состояниях веществ, отличных от стандартных 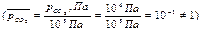 ΔrG1000 =-3,16+8,31. 10 -3 . 1000 ln(1/10-1)=-3,16+19,11=15,95 кДж ˃ 0 - направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10 Па изменилось и самопроизвольное протекание процесса в прямом направлении при заданных начальных условиях и Т=1000 К невозможно.
ΔrG1000 =-3,16+8,31. 10 -3 . 1000 ln(1/10-1)=-3,16+19,11=15,95 кДж ˃ 0 - направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10 Па изменилось и самопроизвольное протекание процесса в прямом направлении при заданных начальных условиях и Т=1000 К невозможно.
∆rG01000 ˂ 0 ˂ ΔrG1000
Химическое равновесие
Реакция является обратимой, если в системе наряду с образованием продуктов происходит превращение продуктов в исходные вещества.
aA(г)+bB(г))  Û eE(г)+ fF(г)
Û eE(г)+ fF(г)
ΔrG < 0 (реакция прямая) ΔrG >0 (реакция обратная)
∆rG = ∆rHТ - T∆rSТ
энтальпийный энтропийный фактор
При некоторых условиях энтальпийный (∆rHТ)и энтропийный фактор (T∆rSТ) могут уравновешиваться и тогда свободная энергия системы (ΔrG) минимальна, а возможность протекания прямой и обратной реакций – равновероятна.
Термодинамическое условие химического равновесия: ∆rG = 0 (p, Т = const) и ∆rF = 0 (v, Т = const)
Кинетическое условие химического равновесияυ прям. = υ обр (равенство скоростей прямой и обратной реакций)
Химическое равновесие –особое состояние системы, при котором состав смеси с течением времени не меняется при неизменных условиях. В этом состоянии: система – равновесная, состав смеси – равновесный, концентрации и парциальные давления – равновесные.
Задача 16
Рассчитайте температуру, при которой равновероятны оба направления реакции (температуру равновесия) и область температур, при которых наиболее вероятно протекание прямой реакции С(к)+ СО2(г)=2СО(г)
Решение:Табличные данные:
| Вещество | ΔfН0298, кДж/моль | S0298, кДж/(моль.K) | ∆fG0298, кДж/моль | Интервал температур, .К |
| С(графит) | 0,0 | 5,74 | 0,0 | (298 – 2300) К |
| СО2 (г) | -393,5 | 213,68 | -394,4 | (298 – 2500) К |
| СО (г) | -110,5 | 197,54 | -137,14 | (298 – 2500) К |
Тсущ. = 2300 К (для наименее устойчивого вещества - графита)
Следствие из закона Гесса: энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов ν
Так, для веществ в стандартных состояниях при Т=298 К (табличная Т)
ΔrН0298 =∑νiΔfНi0 298 продуктов -∑νjΔfНj 0 298 исх веществ=2ΔfН0298 СО(г)- ΔfН0298 С(к) - ΔfН0298 СО2(г)=2(-110,5)–0 –(-393,5) = 172,5 кДж. ΔrН0298 >0 - реакция эндотермическая
S и G – функции состояния и для них:
ΔrS0298 =∑νiS0298,i продуктов-∑νjS0298,j исх веществ=2S0298СО(г)-S0298 С(к)- S0298 СО2(г)= 2(197,54)–5,74–213,68=175,66 Дж/K ΔrS0298 >0 - реакция протекает с увеличением числа молей газообразных веществ ∆νгаз = 2 – 1 = 1>0
Критерий термодинамической возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях – уменьшение энергии Гиббса системы: ∆rGТ < 0
ΔrG0298 = ∑νiΔfG0298,i продуктов - ∑νjΔfG0298,j исх веществ = 2Δf G0298 СО(г) - Δf G0298 С(к) - Δf G0298 СО2(г) =2(-137,14) – 0 – (-394,4) = 120.09 кДж > 0 – самопроизвольное протекание реакции при стандартных состояниях всех участников и Т=298 К в прямом направлении невозможно, реакция будет протекать в обратном направлении.
∆rGТ=∆rНТ - Т∙∆rSТ - энергия Гиббса или изобарно-изотермический потенциал, это функция состояния системы, учитывающая совместное влияние энтальпийного (∆rН) и энтропийного (Т∙∆rS) на самопроизвольное протекание реакции при P, Т = const (свободная энергия).
ΔrG < 0 (реакция прямая), ΔrG >0 (реакция обратная)
∆rG = ∆rHТ - T∆rSТ
энтальпийный энтропийный фактор
При некоторых условиях энтальпийный (∆rHТ) и энтропийный фактор (T∆rSТ) могут уравновешиваться и тогда свободная энергия системы (ΔrG) минимальна, а возможность протекания прямой и обратной реакций – равновероятна.
Термодинамическое условие химического равновесия: ∆rG = 0 (p, Т = const) и ∆rF = 0 (v, Т = const)
Кинетическое условие химического равновесияυ прям. = υ обр (равенство скоростей прямой и обратной реакций).
Химическое равновесие – особое состояние системы, при котором состав смеси с течением времени не меняется при неизменных условиях. В этом состоянии: система – равновесная, состав смеси – равновесный, концентрации и парциальные давления – равновесные.
При температуре равновесия Тр = ∆rH0298 /∆rS0298 = 172,5/175,66.10-3 = 928 K – равновероятно протекание как прямой, так и обратной реакциит.к. при этой температуре ∆rG0Т = 0.
Энтальпийный фактор (стремление системы к упорядоченности) ΔrН0298 =172,5 кДж >0 не способствует протеканию реакции при низких температурах, а энтропийный фактор (стремление системы к хаотичности) Т∙∆r S0298 = Т.175,66 Дж >0 определяет отрицательный знак энергии Гиббса при высоких температурах. Следовательно, область температур, при которых более вероятно протекание прямой реакции при стандартных состояниях веществ (∆rG0Т<0): Тр=982 К < Т < 2300К = Тсущ..
Для равновесной гомогенной системы действует закон действующих масс:
Кс = 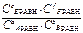 Кp =
Кp = 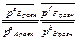
Кс и Кр - константы равновесия (зависят от природы и Т).
Связь между Кр и Кс: Кр = Кс(R*T)∆n (где ∆n =(e+f) – (a+b) - изменение числа молей газов в результате реакции; R* = 0,082 атм.л.моль-1.К-1 ) .
Парциальное давление - 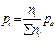 и
и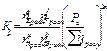
В выражение Кр и Кс гетерогенных систем не входят компоненты в более конденсированном состоянии (в Кр входят только газообразные вещества, а в Кс – жидкие и газообразные).
Чем больше убыль ∆rG, тем сильнее сдвинуто равновесие вправо,тем выше Кp.
∆rG0Т= -RTlnКрдля реакций в газовых системахи ∆rG0Т= -RTlnКс для реакций в конденсированных системах.
Чем больше К, тем выше «выход продукта» (η) – отношение количества (или массы) продукта к максимально возможному его количеству (или массе) при условии полного превращения какого-либо исходного вещества в продукт (100 % превращение невозможно с термодинамической т. зрения т.к. Кр становится ∞)
Кр и Кс не зависят от:
· парциальных давлений
· концентраций компонентов
· общего давления в системе
· но зависят от температуры и природы компонентов системы.
lnKp = -∆rG0Т / RT lnKp = 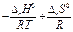
Зависимость константы равновесия от температуры - уравнение изобары Вант-Гоффа в дифференциальной форме: 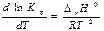 (∆rH0 ¹ f(T) где dlnKp/dT – температурный коэффициент
(∆rH0 ¹ f(T) где dlnKp/dT – температурный коэффициент
После логарифмирования изобары Вант-Гоффа приходим к выражению, связывающему константы равновесия при разных Т и энтальпию реакции 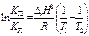
Задача 17
Рассчитать Кр и Кс реакции С(к) + СО2(г) = 2СО(г) при 298 К и 1000 К. ∆rG0298=120кДж; ∆rG01000=-3,16 кДж. Сделайте вывод о выходе продукта реакции и определите знак энтальпии реакции.
Решение Кр= 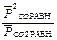 ; Кс=
; Кс= 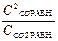 ; ∆rG0Т =- RTlnКр; Kp =exp(-∆G0Т /RT) ; Кс =
; ∆rG0Т =- RTlnКр; Kp =exp(-∆G0Т /RT) ; Кс = 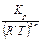
Кр298 = exp(-120.103/8,31.298) = ехр(-48,5) = 8×10-22;
Kp1000 = exp(+3160/8,31.1000) = ехр(0,38) = 1, 46.
∆n = 2-1=1
Кс 298 = 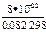 = 3×10-23 Кс 1000 =
= 3×10-23 Кс 1000 = 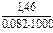 = 0,018
= 0,018
При 298 К - Кр << 1 - в равновесной смеси практически отсутствуют продукты и равновесие смещено в сторону получения исходных веществ.
При 1000 К - Кр > 1 - в равновесной смеси преобладают продукты. Кр растет с увеличением Т. Из уравнения изобары Вант-Гоффа в дифференциальной форме: 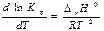 при
при 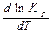 ˃ 0 ∆rH0 >0. Следовательно, реакция эндотермическая.
˃ 0 ∆rH0 >0. Следовательно, реакция эндотермическая.
Задача 18
Для реакции С(к) + СО2(г) = 2СО(г) Кр298 =8×10-22; Kp1000 =1, 46; ΔrН0298 =172,5 кДж.
Объясните увеличение КР с ростом температуры.
Решение :
Зависимость константы равновесия от температуры - уравнение изобары Вант-Гоффа в дифференциальной форме: 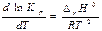
∆rH0Т - стандартная энтальпия реакции, которую в 1-ом приближении считают независимой от Т: ∆rH0 ¹ f(T);
Т. к. ΔrН0298 =172,5 кДж>0 (RT2 >0), то dlnKp/dT ˃0 (температурный коэффициент) - возрастающая функция, поэтому с ростом Т Kp увеличивается.
Задача 19
Определите направление протекания процесса при уменьшении парциального давления исходного газообразного вещества до 10-1 атм при парциальном давлении продукта 1 атм для реакции С(к)+СО2(г)=2СО(г) при Т = 1000 К, если Kp1000 =1, 46.
Решение
