Комплекс түзу реакцияларының тепе-теңдік константалары

Судағы ертіндіде металл иондары гидратталған, яғни аквакомплекс түрінде жүреді М(Н₂О)ⁿ⁺. Ертіндіге комплекс түзетін лигандтарды қосқанда ішкі координациялы сферадан су молекулалары ығыстырылып, олар лигандтармен алмасады:

М(Н₂О)_m + nL ↔ ML_n + mН₂О (7.1)

Реакцияның жазылуын қарапайымдату үшін аквакомплекстердің түзілу және бұзылу процестерін еске алмай, комплекстүзу реакциясы тікелей комплекстүзгіш пен лигандтың арасында жүреді деп қарастыруға болады:

M +nL ↔ ML_n (7.2)

(7.2) реакциясының тепе-теңдік константасы қаншалықты келтірілген реакция аяғына дейін жүретінін көрсетеді, ол комплекстің тұрақтылық константасы (β) деп аталады:

β_n = a _MLn / a_M∙a_Lⁿ (7.3)

ML_n комплексінің түзілуі сатылай жүреді:

M + L ↔ ML₁

ML₁ + L ↔ ML₂

ML₂ + L ↔ ML_3... (7.4)

ML_n-1 + L ↔ ML_n

Әр сатыға сәйкес өзінің сатылай тепе-теңдік константасы болады:

β₁ = 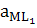/ a_M∙a_L

β₂ = 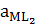/ 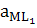∙a_L (7.5)

β₃ = 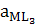/ 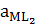∙a_L.......

β_n = 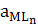/ 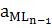∙a_L

β₁, β₂,........ β_n-сатылай тұрақтылық константалары. Келтірілген комплекстүзу реакцияларын басқаша толық реакция түрінде жазуға болады:

M + L ↔ ML₁ β₁ = a_ML / a_M∙a_L

M + 2L ↔ ML₂ β_1,2 = β₁∙β₂= 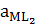/ a_M∙a_L²

M + 3L ↔ ML_3... β_1,3=β₁∙β₂∙β₃= 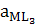/ a_M∙a_L³_..... (7.6)

M+ nL ↔ ML_n β_1,n = β₁∙β₂∙β₃… β_n= 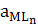/ a_M∙a_Lⁿ

(7.3-7.6) теңдіктерінде келтірілген тұрақтылық константалары компоненттердің активтіктерімен белгіленетіндіктен олар термодинамикалық тұрақтылық константалары болады. Ал концентрациялық тұрақтылық константалары ерітіндінің иондық күшіне байланысты:

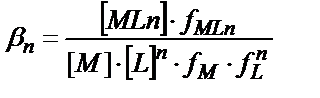
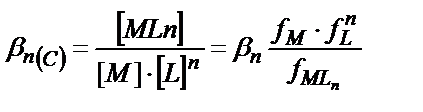(7.7)

Иондық күші тұрақты ерітінділерде концентрациялық тұрақ­тылық константалар мәні өзгермей тұрақты болып қалады, сондықтан β_n(С) пайдаланып тікелей ерітінділердегі тепе-теңдік концентрацияларды есептеуге болады.

Комплекстүзу тепе-теңдігін сипаттау үшін комплексті қосылыстың қаншалықты толық түзілгенін көрсететін функция F(L) (комплекстену функциясы) пайдаланылады. F(L) – металл иондарының жалпы концентрациясы С_м мен оның комплекс түз­беген бөлігінің тепе-теңдік концентрациясының қатынасы ([М]):

F(L) = С_М / [M]

С_М=[M]+ [ML]+ [ML₂]+….. [MLn];

Комплексті иондардың тепе-теңдік концентрацияларын олардың сатылай тұрақтылық константаларын пайдаланып табуға болады, онда:

С_М=[M]+β₁∙[M]∙[L]+β_1,2[M]∙[L]²+…β_1,n[M]∙[L]ⁿ=

=M(1+β₁∙[L]+β_1,2∙[L]²+…β_1,n ∙[L]ⁿ);

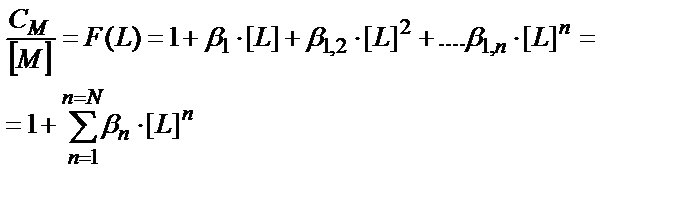N – максималды координациялық сан. Функция F(L) кез-келген комплексті бөлшектердің мольдік үлесін табуға пайдаланылады:

α_MLn = β_n ∙ [L]ⁿ / F(L)

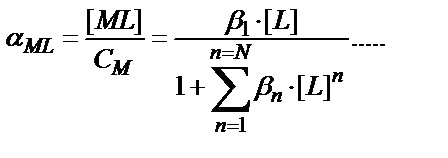
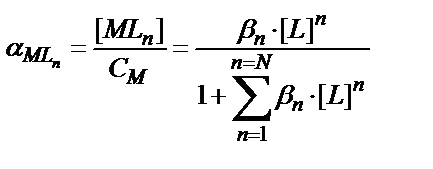(7.8)

Мольдік үлестердің қоспасы бірге тең. Мысалы, Ag⁺+NH₃↔Ag(NH₃)⁺ :

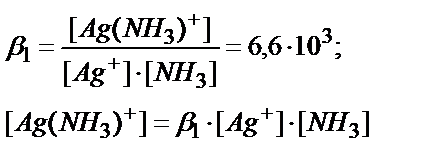
Ag⁺+2NH₃↔[Ag(NH₃)₂]⁺

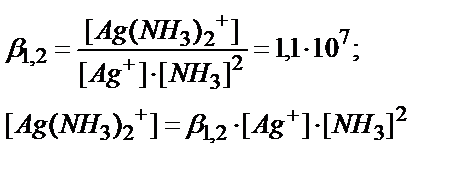
C_Ag+=[Ag⁺]+[Ag(NH₃)⁺]+[Ag(NH₃)₂⁺]=[Ag⁺]+β₁∙[Ag⁺]∙[NH₃]+β_1,2∙[Ag⁺]∙[NH₃]²= [Ag⁺] (1+ β₁∙[NH₃]+β_1,2∙[NH₃]²)

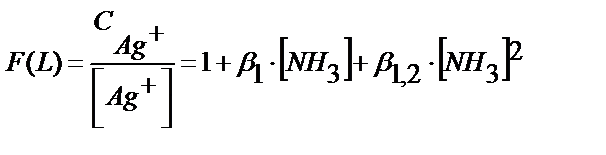
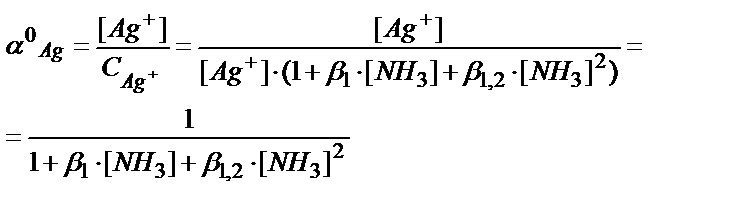(7.9)

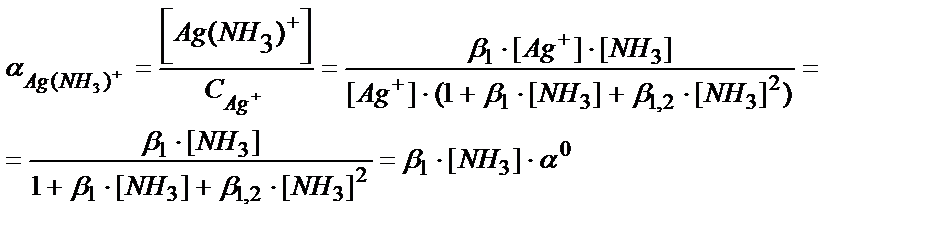(7.10)

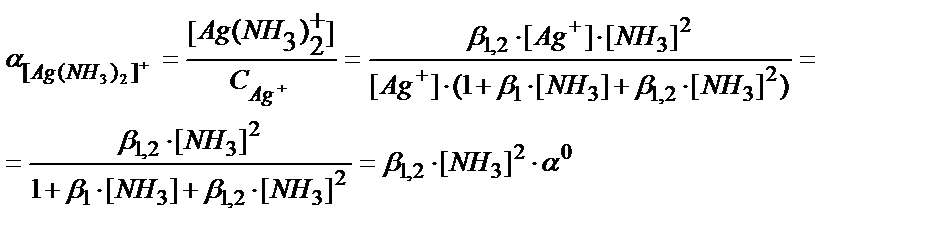(7.11)

Құрамында 0,01М Ag⁺ және 1М NH₃ бар ерітіндідегі комплекстік бөлшектердің тепе-теңдік концентрациясын есептейік. Есепті жеңілдету үшін ерітіндіде лигандтың көп артық мөлшері жүргенде бос лигандтың тепе-теңдік концентрациясын оның алғашқы концентрациясына тең деп алады. Сондықтан [NH₃]= C_NH3=1M.

(7.9) - теңдіктен:

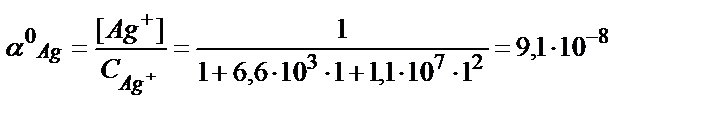
(7.10) - теңдіктен:

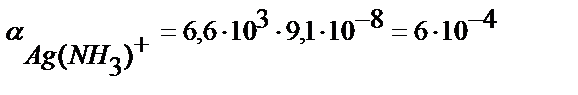
(7.11) - теңдіктен:

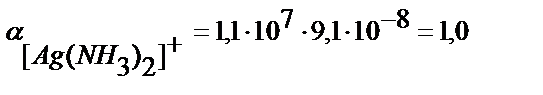
Енді комплекстік бөлшектердің тепе-теңдік концентра­циясын (моль/л) табуға болады. (3.10), (3.11) теңдіктерінен:

[Ag(NH₃)⁺] = C_Ag⁺ ∙ α ([Ag(NH₃)]⁺)=0,01∙6∙10^-4=6∙10^-6 моль/л

[Ag(NH₃)₂⁺] = C_Ag⁺ ∙ α ([Ag(NH₃)₂]⁺)=0,01∙1,0=10^-2 моль/л

Ерітіндіде тек [Ag(NH₃)₂]⁺ бөлшектері жүреді десе де болады, себебі оның концентрациясы [Ag(NH₃)]⁺ бөлшектерінің концентрациясынан мың еседей артық.

Комплекстүзу процесін графикалық жолмен бейнелеу үшін жеке комплекстердің мольдік үлесінің лигандтың концентрациясына тәуелділігін қарастырады: α _MLn – lg [L], не α _MLn - pL(pL=-lg[L]). Ол үшін (7.8) теңдіктері бойынша лиганд концентрация­сының өзгеруіне байланысты әр комплекстің мольдік үлесін есептейді.

7.1 суретте сынаптың (ІІ) хлоридті комплекстерінің таралу, не тепе-теңдік диаграммасы келтірілген. Ерітіндідегі сынаптың хлоридті комплекстері HgCl⁺, HgCl₂, HgCl₃^-, HgCl₄^2-, олардың тұрақтылық константалары β(HgCl⁺)=5,5∙10⁶; β(HgCl₂)=1,6∙10¹; β(HgCl₃^-) = 1,2∙10¹⁴; β(HgCl₄^2-) = 1,2∙10¹⁵_.

Әр комплекстің мольдік үлесі:

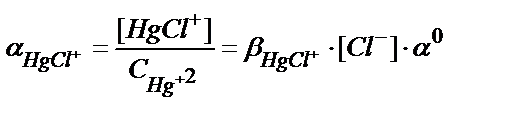
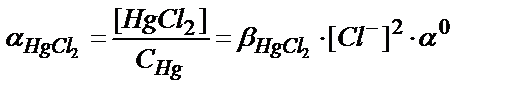
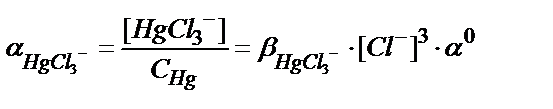
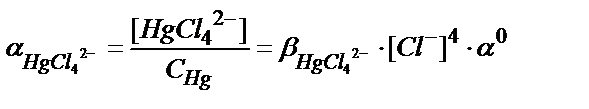
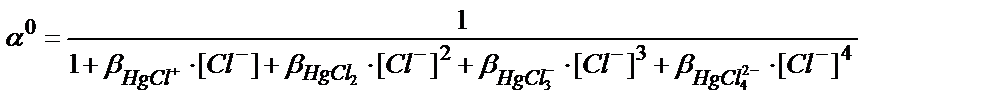
7.1 суреттен хлор иондарының концентрациясы өзгеруіне байланысты ерітіндіде басым жүретін негізгі комплекс HgCl₂ екенін байқауға болады.

0,2

0,4

0,6

0,8

10-1 -3 р[L]

α

Нg2+

HgCl42-

НgCl2-

НgCl3 -

HgCl+

7.1 – сурет. Сынап(ІІ)-ионының хлоридті комплекстерінің таралуы, не тепе-теңдік диаграммасы.

Комплексті қосылыс ерітіндісіндегі тепе-теңдікті комплекстің диссоциациялануы тұрғысында қарастыруға болады:

ML_n↔M+nL, 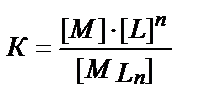– тұрақсыздық константасы.

Тұрақсыздық константасы тұрақтылық константаға кері мән: ;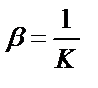

Комплекс түзетін М және L компоненттердің тек өзара әрекеттесуі тәжірибеде өте сирек кездеседі. Көбінесе ерітіндіде М және L –мен қосымша реакцияға қатысатын заттар жүреді. Мысалы, сулы ерітіндінің қышқылдығы металл иондарының гидроксокомплекс, ал лигандтардың протонданған қосылыстар түзуіне себеп болады:

М+ nOH^- ↔ M(OH)_n (7.12)

L+mH₃O⁺↔H_mL+mH₂O (7.13)

(7.12), (7.13) реакциялары жүйедегі М және L концен­трацияларына әсер етіп негізгі (7.2) процесінің жүру жағдайын өзгертеді. Ерітіндіде жүретін қосымша реакцияларды ескеру үшін шартты тұрақтылық константаларын пайдаланған жөн:

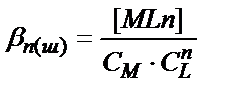(7.14)

С_М – құрамында М бар бөлшектердің концентрациясы. Бұл мәнге негізгі лиганд L- мен байланысқан бөлшектер кірмейді:

С_М= [M]+[M(OH)]+[M(OH)₂]+….[M(OH)n] (7.15)

Сол сияқты С_L – М-мен байланысқан түрлеріне басқа құрамында L бар қосылыстардың қоспасы:

С_L= [L]+[HL]+[H₂L]+….[H_mL] (7.16)

(7.15), (7.16) теңдіктерінде бөлшектердің зарядтары жазыл­ма­ған.

Шартты тұрақтылық константасын есептеу үшін қосымша реакциялардың коэффициенттерін білу керек – α_М, α_L:

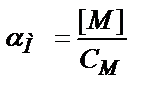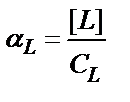; (7.17)

(7.14) теңдігіндегі С_М және C_L мәндерін (7.17) мәндерімен алмастырса:

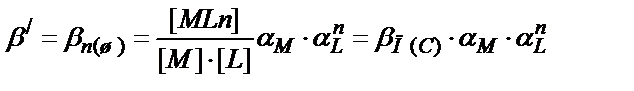(7.18)

α_М, α_L- М және L бөлшектерінің белгілі жағдайдағы мольдік үлесін көрсетеді.

Α_М және α_L коэффициенттерін есептеуді қарастырайық. (7.15) теңдігіне кіретін МОН, М(ОН)₂ т.б. бөлшектерінің концентрацияларын әр комплекске сәйкес тұрақтылық константаларын пайдаланып табуға болады:

β₁= [MOH]/[M]∙[OH]; [M(OH)]= β₁∙[M] ∙[OH]

β₂= M(OH)₂/[M]∙[OH]²; [M(OH)₂]= β₂∙[M]∙ [OH]²

………………………………………………………………..

Β_n= [M(OH)_n] / [M]∙[OH]ⁿ [M(OH)_n]= β_n[M]∙[OH]ⁿ (7.19)

Осыдан:

См=[M]+β₁∙[M]∙[OH]+β_1/2∙[M]∙[OH]²+…β_1/n[M]∙[OH]ⁿ=

=[M]∙(1+β₁∙[OH]+β_1/2∙[OH]²+… β_1/n∙[OH]ⁿ )

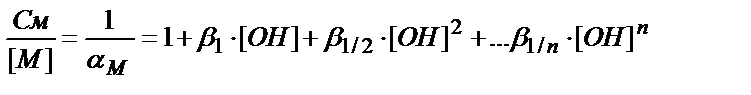
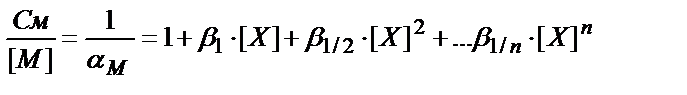(7.20)

Егер МХ, МХ₂ т.б. комплекстерінің тұрақтылық констан­талары және лиганд Х-тің концентрациясы белгілі болса α_м мәнін жеңіл есептеуге болады. Сол сияқты α_L да есептеуге болады. Пайда болатын қышқылдың жалпы формуласын Н₄L дейік, онда НL, Н₂L, H₃L, H₄L бөлшектерінің концентрациялары әрқайсысына сәйкес сатылай қышқылдық константалармен анықталады:

Н₄L ↔ H₃L^- + Н⁺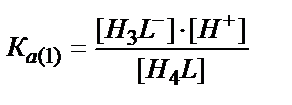

H₃L^- ↔ H₂L^2- + Н⁺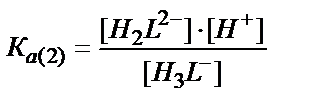

H₂L^2-↔ HL^3- + Н⁺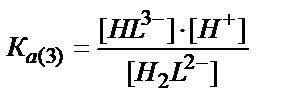

HL^3- ↔ L^4- + Н⁺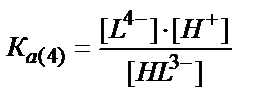

[HL^3-] ↔ [L^4-] ∙ [Н⁺] /K_A(4)

[H₂L^2-]↔ [HL^3- ]∙[Н⁺] /K_A(3)

[H₃L^-] ↔ [H₂L^2-] + [Н⁺] /K_A(2) (7.21)

[Н₄L] ↔ [H₃L^-]+[Н⁺] /K_A(1)

(7.21) теңдігіне [HL^3-] мәнін қойсақ:

[H₂L^2-]=[L^4-] ∙ [Н⁺]²/ K_A(3)∙K_A(4) (7.22)

(7.22) теңдігіне [H₂L^2-] мәнін қойсақ:

[H₃L^-]=[L^4-] ∙ [Н⁺]³/ K_A(4)∙K_A(3)∙K_A(2) (7.23)

(7.23) теңдігіне [H₃L^-] мәнін қойсақ:

[H₄L]=[L^4-] ∙ [Н⁺]⁴/ K_A(1)∙K_A(2)∙K_A(3)∙ K_A(1) (7.24)

(7.21-7.24) теңдіктеріндегі [HL^3-], [H₂L^2-], [H₃L^-], [Н₄L] мән­дерін (7.16) теңдігіне қойсақ:

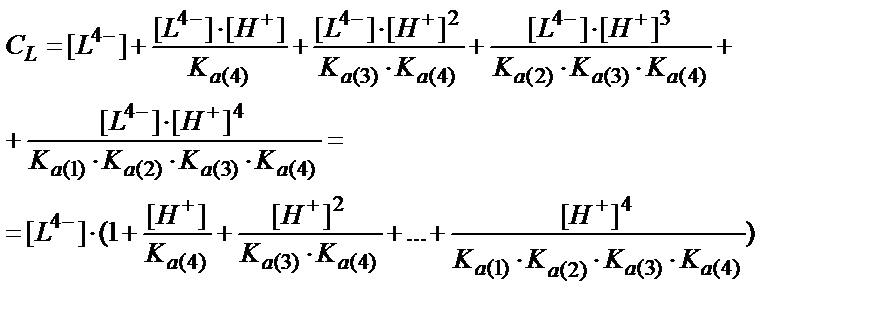
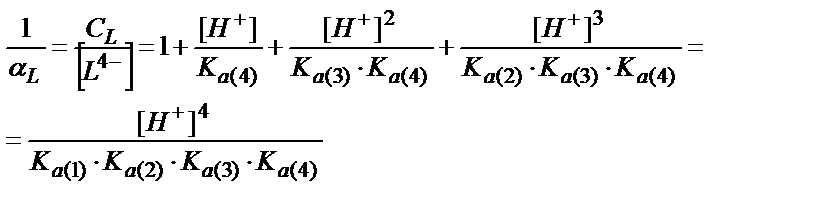
Мысалы, мыс иондарының этилендиаминтетрасірке қышқылымен (ЭДТУ) ерітінді рН=3 болғандағы түзетін комплекстің шартты тұрақтылық константасын табайық, ЭДТУ төрт негізді қышқыл (Н₄У):

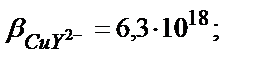
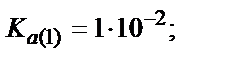
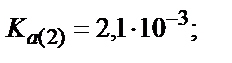
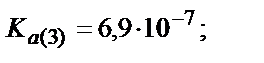
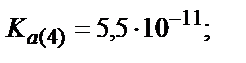
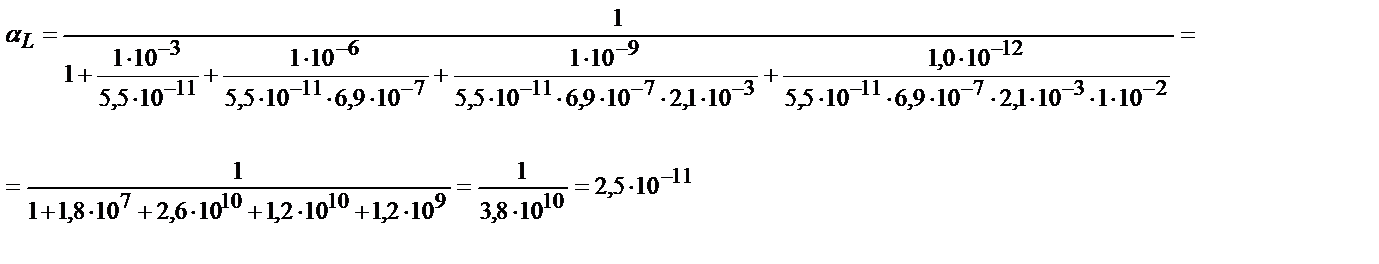
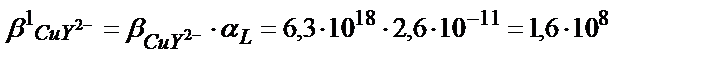
Комплекстің тұрақтылығы 10¹⁰ есе кемиді.

Егер М мен L екеуі де қосымша реакцияға қатысса β¹ (7.18) теңдігімен есептеледі. Мысалы, 1,0 ∙10^{-3 М НСl ерітіндісіндегі HgY2-} комплексінің тұрақтылық константасын табайық. Бұл жағдайда екі түрлі (бәсекелес) реакция жүреді: 1) Hg(II)-ионының хлоридті комплекстер түзуі; 2)Y^4--ионының протондану реакциялары.

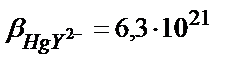, сынаптың (ІІ) хлоридті комплекстерінің тұрақтылық константалары: β₁= 5∙10⁶; β₂= 1,6∙10¹³; β₃= 1,2∙10¹⁴; β₄= 1,2∙10¹⁵.

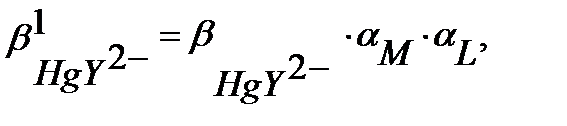α_L мәні бұдан бұрынғы келтірілген мысалдардан 2,6∙10^-11.

(7.20) теңдігінен

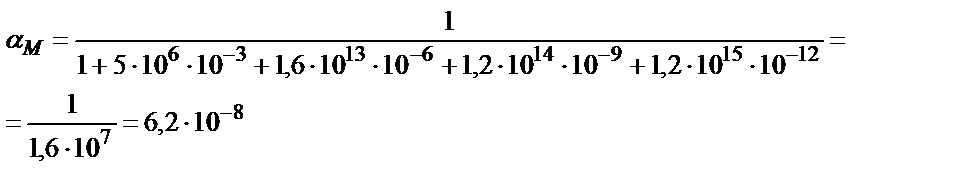
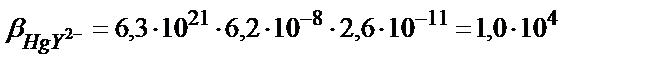
Келтірілген мысалдардан комплексті қосылыс алу үшін ерітіндідегі қосымша реакцияларды еске алып белгілі жағдайлар жасау қажет.

Тұрақтылық константаларын табуға, тәжірибелік мәндерді пайдаланып жеңіл есептелетін және тұрақтылық константаларымен күрделі математикалық байланысы бар функциялар пайдаланылады. Мұның бірі Бьеррум ұсынған «түзілу функциясы» 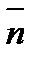. 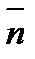- комплекс түзгішпен байланысқан лигандтардың орта саны:

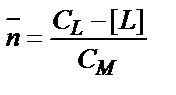
Лигандтардың жалпы концентрациясы С_L бос лиганд пен жеке комплекстердің лигандтың санына көбейтілген концентрацияларының қосындысына тең:

C_L= [ML]+2[ML₂]+3[ML₃]+….+n[ML_n]+[L]

C_L-[L] = [ML]+2[ML₂]+ 3[ML₃]+….+n[ML_n];

(C_L-[L]) – комплекстүзгішпен байланысқан лигандтардың концентрациясы. Бұл теңдікке кіретін комплекстердің концентрациясын толық тұрақтылық константаларын (7.6) пайдаланып табады:

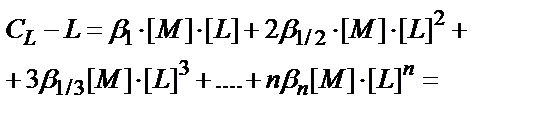
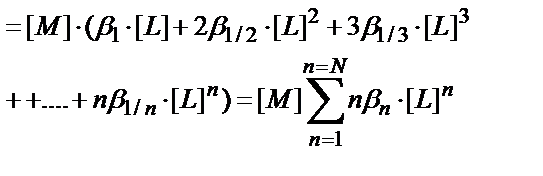(7.25)

Комплекстүзгіштің жалпы концентрациясы

См= [M]+[ML] + [ML₂] + [ML₃] + ….+[ML_n];

(7.6) теңдігінен:

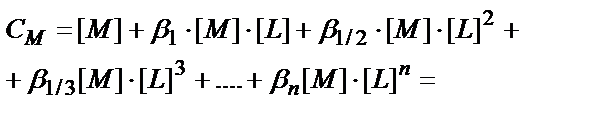
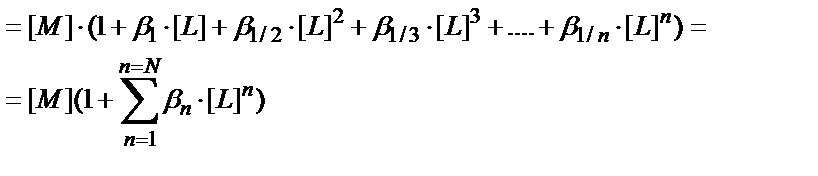(7.26)

(7.25) теңдігінің (7.26) теңдігіне қатынасы түзілу функциясы мен бос лигандтардың арасындағы байланысты береді:

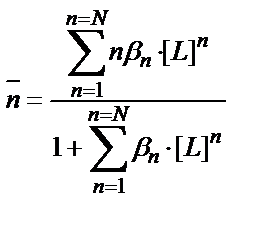
Бос лигандтың концентрациясының өзгеруі түзілу функциясы мәнін өзгертеді.