Упрощенная теория нормального распространения пламени

Скорость нормального распространения пламени теорети­чески может быть определена из решения уравнения теплопроводности, если известно кинетическое уравнение реакции. Решение для U_n впервые было получено в 1938 году Зель­довичем Я.Б. и Франк-Каменецким Д.А., которые разработали тепловую теорию ламинарного распространения пламени. На основе физической модели тепловой теории устанавливаются простые соотношения, связывающие нормальную скорость сгорания с размерами зоны горения и характеристиками пламени.

Поток тепла, отнесенный к единице поверхности в едини­цу времени, пропорционален градиенту температуры (закон теплопроводности Фурье):

q = - λ_м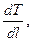

где λ_м – коэффициент молекулярной теплопроводности, Дж/с·м·град. Знак "-" учитывает то, что тепловой поток имеет направление, обратное направлению повышения температуры.

Рассмотрим элемент фронта пламени. Если принять, что изменение температуры подчиняется линейному закону (пунктир на рис.3.8), то можем написать:

Рис.3.8. Структура ламинарного фронта пламени

Этот тепловой поток воспринимается несгоревшей смесью и идет на повышение её температуры от Т₀ до Т_Г .

q_{2 = W·}ρ₀·c_p·(T_Г – T₀);

Так как q₁ = q₂ и W = U_n, то

U_n·ρ₀· c_p·(T_Г – T₀) = λ_м 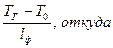U_n = λ_м/c_p· ρ₀· .

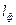Здесь а_м = λ_м / c_p · ρ₀ - коэффициент молекулярной температуропроводности, см²/с

Химическая ширина зоны горения составляет долю от фи­зической

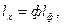где ф < 1

Это функция, зависящая от скорости химической реакции, поэтому

U_n = ф 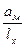(3.4)

Последнее выражение показывает, что чем меньше толщина зоны горения, тем больше нормальная скорость горения U_n.

Фронт пламени, движущийся со скоростью U_n, будет прохо­дить расстояние ℓ_х, за время сгорания τ_х .

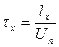(3.5)

Подставляя значение ℓ_х= U_n· τ_х в (3.4), получим:

U_n² = ф /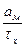

Считая, что ℓ_х ≈ ℓ_ф получим окончательно:

U_n 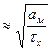(3.6)

или τ_х ≈ а_м/ U_n²;

подставляя последнее выражение в (3.5), получаем:

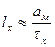(3.7)

Полученное выражение дает возможность лишь ка­чественно оценивать влияние различных величин на U_n.

Нормальную скорость сгорания и ее зависимость от качес­тва и состава смеси, температуры и давления определяют экспериментально. В настоящее время это проще и точнее теоретического расчета.

На рис. 3.9 приведены экспериментальные данные зависимо­сти U_n бензо- и керосиновоздушных смесей от коэффициента избытка воздуха при различных начальных температурах. Максимальное значение U_n достигается не при стехиометрическом, а при несколько более богатом составе смеси (α ≈ 0,9 - 0,95), и в обе стороны от этого значения вели­чина U_n снижается, так как недостаток либо горючего, либо окислителя приводит к снижению температуры сгорания и уменьшению U_n. Распространение пламени при умеренной Т₀ происходит в диапазоне α от 0,6 до 1,7. Более бедная и более богатая топливная смесь не горит. С увеличением тем­пературы U_n возрастает.

Достижение U_{n мах} при α < 1 наблюдается и для других горючих смесей. Объясняется это следующим:

1. В точке, где U_{n мах} достигается максимальная тем­пература сгорания. При некотором обогащении состава смеси топливом от стехиометрического более полно используется кислород воздуха. При стехиометрическом составе смеси по­является большая вероятность того, что не весь кислород воздуха из-за микронеоднородностей смеси будет использован. В результате не сгорит и все топливо, температура окажется несколько меньше, чем теоретическая.

2. При α ≤ 1 несколько возрастает скорость химической реакции, так как на богатой смеси более вероятно образова­ние активных центров ОН и Н ,способствующих возникновении новых цепей, и следовательно, увеличению скорости реакции.

При увеличении начальной температуры топливовоздушной смеси нормальная скорость горения возрастает (рис.3.10), что согласуется с выводами рассмотренной выше тепловой теории - с увеличением начальной температуры возрастает величина коэффициента температуропроводности и уменьшается время химической реакции, так как возрастает ее скорость. Но скорость химической реакции возрастает от температуры по экспоненте, а величина U_n по зависимости, близкой к квадратичной.

U_nTг = U_nT0·(T_Г/T₀)^m, где m = 1,5 – 2,0, U_{n То} - нормальная скорость при Т₀ = 288° K.

Зависимость U_n от давления различна для разных смесей. Для смеси углеводородного топлива с воздухом

U_np = U_n0/pⁿ, где n = 0,2 – 0,3; U_{n 0} - нормальная скорость при p = 1 кг/см².

Для топливокислородных смесей по данным некоторых ис­следователей n = 0, то есть U_n не зависит от давления. При разбавлении горючей смеси инертными газами (С0₂, N₂, Не, Аr и др.) нормальная скорость сгорания уменьшается. Это в первую очередь объясняется тем, что при добавлении инертного газа уменьшается концентрация реагирующих ве­ществ и соответственно падает скорость химической реакции. Помимо этого, может изменяться коэффициент температуропроводности.

На рис. 3.11 приведен график, показывающий как будет изменяться нормальная скорость пропано-кислородо-азотной смеси, если между пропаном (С₃Н₈ ) и кислородом выдерживается стехиометрическое соотношение (α = 1), но будет изменяться мольная доля кислорода ψ. Для воздуха ψ = 0,21. При большой доле кислорода U_n растет пропорционально ψ .

Рис.3.9. Зависимость U_n от α при различ­ных начальных температурах (бензиновоздушная смесь)

Рис.3.10. Зависимость U_{n max} от t₀ для смесей с различными горючими веществами

Рис. 3.11. Зависимость U_n от нейтральной примеси (см/с)