Определение растворимости малорастворимого соединения

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Раствор, находящийся в равновесии с твердым веществом, называется насыщенным раствором, а его концентрация – растворимостью твердого вещества.

В насыщенном растворе существует равновесие между твердым соединением и его раствором:

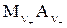
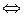ν₊М^z+ + ν_– А^z- (1)

Твердая фаза Ионы в растворе

Для процесса растворения константа равновесия К_а выражается уравнением

К_а = 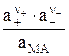= 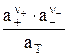, (2)

где 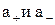– активности катиона и аниона соответственно; а_МА= а_Т – активность твердого соединения.

Активность твердого соединения а_Т = 1, следовательно при данной температуре произведение 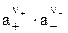есть постоянная величина, которая называется произведением растворимости ПР

ПР= 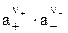. (3)

Принимая во внимание, что, а_i = g_i·c_i , где а_i, g_i и c_i – активность, коэффициент активности и концентрация i – го иона, запишем

ПР= 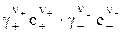. (4)

Для малорастворимых соединений концентрация растворенного вещества в растворе мала и коэффициенты активности ионов не зависят от их концентраций и могут быть включены в постоянную ПР, а при отсутствии в растворе других ионов, будут равны 1. В обоих случаях произведение растворимости можно представить в виде:

ПР = 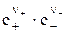= = 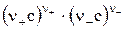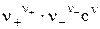, (5)

где с – концентрация соединения в насыщенном растворе, моль/дм³;

ν = ν₊ + ν_–.

Если в растворе кроме ионов малорастворимого соединения присутствует заметное количество других ионов, активность которых нельзя считать равной концентрации, ПР нужно рассчитывать по уравнению (4). Поскольку невозможно найти коэффициент активности отдельного иона с помощью закона Дебая – Хюккеля определяют средний коэффициент активности электролита g_±, который связан с коэффициентами активности отдельных ионов:

lg g_± = –0,509 |z₊·z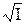_-| (6)

где z_i – заряд иона;

I = 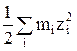– ионная сила раствора;

m_i – моляльная концентрация i-го иона;

g_± = .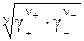

В общем случае произведение растворимости связано с концентрацией с насыщенного раствора электролита уравнением

ПР = 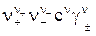. (7)

Здесь принято, что степень диссоциации растворенного соединения равна 1.

Для бинарного электролита ν₊ = ν_– = 1 и формулы (1) – (7) упрощаются.

В предельно разбавленных растворах, которыми и являются растворы малорастворимых соединений, зависимость растворимости от температуры при постоянном давлении выражается уравнением

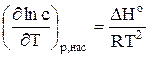, (8)

где ΔН^о – дифференциальная теплота растворения соединения, Дж/моль;

R – универсальная газовая постоянная, Дж/(моль·К).

Интегрирование уравнения (8) в малом интервале температур, когда можно считать величину ΔН^о постоянной, дает

ln с= 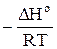+ const . (9)

Используя уравнение (9), можно определить дифференциальную теплоту растворения малорастворимых соединений. Построив график в координатах ln с – 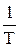и обработав его уравнением прямой линии, используя метод наименьших квадратов, получим

ln с = к 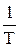+ b . (10)

Из сравнения уравнений (9) и (10) следует, что коэффициент к = ,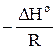

тогда

ΔH^o = – к·R . (11)

Изменение свободной энергии Гиббса ΔG^о при растворении соединения в насыщенном растворе зависит от величины произведения растворимости

ΔG°= – RT ln ПР (12)

Для изменения энтропии ΔS^о в процессе растворения имеем:

ΔS° = 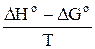. (13)

Определить растворимость малорастворимых соединений можно методом электропроводности.

Для этого при различных температурах экспериментально определяют величину удельной электропроводности 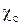насыщенного раствора исследуемого соединения и рассчитывают предельную молярную электропроводность λ_о этого же раствора (прибесконечном его разведении) по уравнению

λ_о = [λ₊ + b₊ (t – 25) + λ _–+ b_– (t – 25)], (14)

где λ₊ и λ _– – предельные молярные электропроводности катионов и анионов соответственно, См·м²/моль; t – температура , ^оС; b₊ и b_– – температурные коэффициенты электропроводности катиона и аниона при температуре 25 ^оС. Величины λ₊ , λ _– ,b₊ и b_– берут из справочника.

Концентрацию соединения в насыщенном растворе при различных температурах рассчитывают по уравнению:

с = 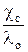(15)

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Цель работы: установить ПР, ΔН^о, ΔG^о и ΔS^о малорастворимой соли.

Для определения удельной электропроводности насыщенного раствора малорастворимой соли используют кондуктометр. Чтобы по результатам измерений можно было рассчитать истинную удельную электропроводность, измерительную ячейку градуируют по стандартному раствору хлорида калия и рассчитывают постоянную ячейки по уравнению

R = 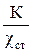, (16)

где К – постоянная ячейки; χ_ст – известная удельная электропроводность стандартного электролита, См/м.

В качестве стандартного раствора применяют водные растворы хлорида калия определенных концентраций, удельная электропроводность которых известна.

Порядок выполнения работы

1. Готовят стандартный раствор хлорида калия концентрацией 0,001 М.

2. Измеряют сопротивление воды, используемой для приготовления растворов.

3. Приготовленным раствором хлорида калия сначала ополаскивают, а затем заполняют измерительную ячейку, которую помещают в термостат на 20 – 30 минут.

4. Измеряют сопротивление растворов хлорида калия при температурах 30, 35, 40, 45 °С и по уравнению (16) рассчитывают постоянные сосуда.

Внимание. Объем раствора в ячейке должен быть постоянным во всех измерениях.

5. Готовят насыщенный раствор малорастворимой соли. Выбор соли обусловлен заданием преподавателя. Небольшое количество соли растирают в ступке, помещают в коническую колбу с притертой пробкой и два-три раза промывают дистиллированной водой для удаления легкорастворимых примесей. Отмытую соль заливают водой (100 мл) и, плотно закрыв колбу пробкой, непрерывно взбалтывают в течение 20 мин. Полученную суспензию отфильтровывают через стеклянный фильтр, а осадок используют для приготовления насыщенного раствора. Готовят еще такой же насыщенный раствор, и полученную суспензию профильтровывают через осадок, специально нанесенный на фильтр. Такое фильтрование предупреждает образование пересыщенного раствора малорастворимой соли.

6. Раствор сливают в измерительную ячейку, которую погружают в термостат с температурой 30 °С, и после установления температуры раствора измеряют его электросопротивление R_t , а затем по уравнению

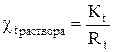(17)

рассчитывают удельную электропроводность χ _{t раствора} при заданной температуре, используя значение постоянной ячейки K_t при этой же температуре.

7. Повторяют измерение сопротивления и последующие расчеты для температур 35, 40 и 45 ^оС.

8. Рассчитывают мольную электропроводность λ_о этого же раствора прибесконечном его разведении по уравнению (14) для температур 30, 35, 40, 45 ^оС.

Экспериментальные и рассчитанные величины вносят в таблицу.

Таблица 1. Экспериментальные и рассчитанные результаты.

Температура, К	Постоянная ячейки, м-1	Удельная электропроводность воды, См/м	Сопротивление раствора, Ом	Удельная электропроводность раствора, См/м	Мольная электпроводность, См·м2/моль

Обработка результатов опыта

1. По уравнению (15) рассчитывают растворимость соли, а по уравнению (7) находят ПР для трех температур.

2. Строят график в координатах ln c – 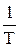, обрабатывают его уравнением прямой линии и, используя коэффициент к уравнения регрессии, рассчитывают дифференциальную теплоту растворения соли ΔН^о по выражению (11).

3. Используя уравнения (12) и (13), находят ΔG^о и ΔS^о.

Рассчитанные величины вносят в таблицу.

Таблица 2. Результаты расчета.

Температура, К	Растворимость соли, моль/м3	Произведение растворимости	ΔНо, кДж/моль	ΔGо, кДж/моль	ΔSо, Дж/(моль·К)

По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Напишите уравнение зависимости растворимости ионизированной соли от температуры.

2. Дать определение удельной и молярной электропроводностей раствора электролита.

3. Как можно рассчитывать дифференциальную теплоту растворения соли?

4. Как устанавливается постоянная измерительной ячейки?

5. Напишите уравнение для расчета ΔН^о, ΔG^о, ΔS^о процесса растворения.

6. Выражение для произведения растворимости.

7. Как рассчитывается ионная сила раствора?

8. Уравнение связи ионной силы раствора и среднего коэффициента активности электролита.

9. Напишите уравнение для константы равновесия процесса растворения.

10. Зависимость константы равновесия процесса растворения от температуры.

11. Размерности величин в уравнениях.

РАБОТА 7

ОПРЕДЕЛЕНИЕ СТАНДАРТНОГО ОКИСЛИТЕЛЬНО-