П 6. Расчет энтропии химической реакции. Расчет энергии Гиббса.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

П 5. Энергетические эффекты химических процессов.

Термохимические расчеты. Расчет теплоты сгорания топлива.

Пример 1.Термохимическое уравнение реакции. Энтальпии образования вещества.

Напишите термохимическое уравнение реакции, которое отвечает энтальпии образования H₂SO₄(ж).

Решение.Химические уравнения реакций, в которых указаны агрегатные состояния веществ и тепловые эффекты, называются термохимическими уравнениями.

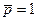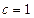Стандартной энтальпией (теплотой) образования веществаназывается энтальпия образования 1 моля вещества из простых веществ, если все участники реакции находятся в стандартных состояниях (с.с. при и моль/л), (Δ_fН⁰₂₉₈ см.Приложение 2, [1]

По определению, искомое уравнение должно состоять из исходных простых веществ, устойчивых в стандартном состоянии:

H₂(г) + 2O₂(г) + S(к) = H₂SO₄(ж) , Δ_fН⁰_{298 H2SO4} = −811,3 кДж/моль.

Из табл. (Приложение 2, [1]).

Отрицательное значение энтальпии образования соединения указывает на то, что в результате образования этого соединения из простых веществ теплота выделяется.

Пример 2. Взаимосвязь изменения энтальпии и внутренней энергии в результате реакции.

Рассчитайте изменение внутренней энергии системы при изохорно-изотермическом протекании реакции

С(к) + СО₂(г) = 2СО(г)

при с.с. и 298 К.

Решение. Внутренняя энергия системы U – одна из термодинамических функций состояния системы. Изменение внутренней энергии в результате какого-либо процесса (например, химической реакции) Δ_rU равно тепловому эффекту этого процесса, протекающего в изохорно-изотермических условиях (Q_V,T ), если при этом не совершается никакой работы:

Q_V,T = - Δ_rU .

Энтальпия Н – одна из термодинамических функций состояния системы.

Изменение энтальпии в результате какого-либо процесса (химической реакции) Δ_rН равно тепловому эффекту этого процесса, протекающего в изобарно-изотермических условиях (Q_p,T), когда единственным видом работы является работа расширения газа:

Q_p,T = - Δ_rH_Т.

Изменение энтальпии и внутренней энергии в результате реакции связаны соотношением:

Δ_rН =Δ_rU + ∆νRT,

где ∆ν – разница между числом молей газообразных продуктов и числом молей газообразных исходных веществ.

Если Δ_rН < 0, то процесс идет с выделением тепла в окружающую среду и реакция называется экзотермической; если Δ_rН > 0, теплота в результате реакции поглощается и реакция называется эндотермической.

Согласно данным (Приложение 2, [1] ):

Вещество Δ_fН⁰₂₉₈,кДж/моль

С(графит) 0

СО₂ (г) −393,5

СО (г) −110,5

Для расчета энтальпии химической реакции при с.с. и 298 К воспользуемся следствием из закона Гесса:

Δ_rН⁰₂₉₈= ∑ν_iΔ_f Н⁰_{298, продуктов} − ∑ν_jΔ_f Н ⁰_{298, исх веществ} ;

Δ_rН⁰₂₉₈ = 2Δ_fН⁰_298СОг − Δ_fН⁰_298Ск − Δ_fН⁰_298СО2г = 2(−110,5) – 0 – (−393,5) =

= 172,5 кДж. Так как Δ_rН⁰₂₉₈ > 0, данная реакция эндотермическая.

Изменение энтальпии и внутренней энергии в результате реакции связаны соотношением:

Δ_rН =Δ_rU + ∆νRT .

Тогда ∆_rU⁰₂₉₈ = ∆_rH⁰₂₉₈ – ∆νRT =

= 172,5 – 1·8,31·298·10⁻³ = 170,02 кДж. (Разница между числом молей газообразных продуктов и исходных веществ равна ∆ν = 2 − 1 = 1 моль).

Универсальная газовая постоянная R=8,31 Дж/моль^.К.

Пример 3. Закон Гесса. Метод циклов.

Вычислите тепловой эффект образования NH₃ из простых веществ при стандартном состоянии по тепловым эффектам реакций:

2H₂ + O₂ = 2H₂O_(ж);; D_r H⁰₁ = - 571,68 кДж (1)

4 NH₃ + 3 O₂ = 6 H₂O_(;ж) + 2 N₂ ; D_r H⁰₂ = - 1530,28 кДж (2).

Решение. Закон Гесса: Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий.

Запишем уравнение реакции, тепловой эффект которой необходимо определить:

½N₂ + 3/2Н₂ = NH₃ ; D_r H⁰₃ = D_f H⁰_NH3= ?;(3).

В уравнения (1) и (2) входят Н₂О (ж) и О₂, которые не входят в уравнение (3), поэтому, чтобы исключить их из уравнений (1) и (2), умножим уравнение (1) на 3 и вычтем из него ур (2):

6Н₂ + 3О₂ – 4NН₃ – 3О₂ = 6Н₂О (ж) – 6Н₂О (ж) – 2N₂ (г) (4).

После преобразования уравнения (4) и деления его на 4 получаем искомое уравнение (3). Аналогичные действия проделаем с тепловыми эффектами:

(3D_rH⁰₁– D_rH⁰₂)/4 = D_rH⁰₃. В результате получаем:
D_r H⁰₃ = [3(–571,68) – ( – 1530,28)] / 4 = – 46,19 (кДж);

т.е. ∆ _f Н⁰ _NH3 = – 46,19 кДж/моль.

Пример 4.Закон Гесса. Метод циклов.

Определите стандартный тепловой эффект реакции:

С(к) + СО₂(г) = 2СО(г); (1),

если известны тепловые эффекты двух других реакций:

2С(к) + О₂(г) = 2СО(г) ; ∆_rH⁰₂₉₈ = −221 кДж (2)

и

2СО(г) + О₂(г) = 2СО₂(г); ∆_rH⁰₂₉₈ = −566,1 кДж (3).

Решение.Закон Гесса: Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий.

Для того, чтобы получить уравнение реакции (1), нужно из уравнения реакции (2) вычесть уравнение реакции (3) и разделить полученное выражение на 2. Те же действия следует проделать и с величинами ∆_rH⁰.

Имеем ∆_rH⁰₁ = (∆_rH⁰₂ − ∆_rH⁰₃)/2 = [−221 – (−566,1)]/2 = 172,5 кДж.

Пример 5. Расчет стандартной энтальпии химической реакции при различных температурах.

Рассчитайте стандартный тепловой эффект изобарно-изотермической реакции

С(к) + СО₂(г) = 2СО(г)

при 298 К и при 1000 К , считая постоянными теплоемкости реагентов в данном температурном интервале.

Решение. Запишем значения стандартной энтальпии образования и стандартной теплоемкости веществ согласно данным (Приложение 2, [1] ):

Вещество Δ_fН⁰₂₉₈,кДж/моль С⁰_р298, Дж/моль^.К

С(графит) 0 8,54

СО₂ (г) −393,5 37,41

СО (г) −110,5 29,14

Для расчета энтальпии химической реакции при с.с. и 298 К воспользуемся следствием из закона Гесса:

Δ_rН⁰₂₉₈= ∑ν_iΔ_f Н⁰_{298, продуктов} − ∑ν_jΔ_f Н ⁰_{298, исх веществ} ;

Δ_rН⁰₂₉₈ = 2Δ_fН⁰_298СОг − Δ_fН⁰_298Ск − Δ_fН⁰_298СО2г = 2(−110,5) – 0 – (−393,5) =

= 172,5 кДж. Так как Δ_rН⁰₂₉₈ > 0, данная реакция эндотермическая.

Зависимость энтальпии реакции от температуры в области 298 ÷Т, в которой нет фазовых переходов, в интегральном виде выражается уравнением Кирхгофа:

_Т

∆_rH⁰_T = ∆_rH⁰₂₉₈ + ∫ ∆_rС⁰_pdT ,

²⁹⁸

где ∆_rН⁰₂₉₈ − стандартная энтальпия реакции при 298К; ∆_rС_p⁰ − изменение стандартной теплоемкости системы в ходе реакции.

Если пренебречь зависимостью С_р реагирующих веществ от Т, то есть

∆_rС⁰_p = const, то имеем приближение в виде:

∆_rН⁰_Т = ∆_rН⁰₂₉₈ + ∆_rС⁰_р(Т − 298) ,

рассчитать ∆С⁰_р можно по справочным данным, как разность стандартных изобарных теплоемкостей продуктов и исходных веществ при 298 К.

Рассчитаем изменение теплоемкости системы в результате реакции:

∆_rС⁰_р = 2С⁰_р298СОг – С⁰_р298Ск – С⁰_р298СО2г = 2(29,14) – 8,54 – 37,41 = 12,33 Дж/К.

По уравнению

∆_rН⁰_Т = ∆_rН⁰₂₉₈ + ∆_rС⁰_р(Т − 298)

рассчитаем энтальпию химической реакции при с.с. и 1000 К:

∆_rН⁰₁₀₀₀ = 172,5 + 12,33·10⁻³(1000 − 298) = 172,5 + 8,66 = 181,16 кДж.

Из расчетов следует, что при изменении температуры на 702 К увеличение теплового эффекта составляет всего около 5%.

Пример 6. Расчет тепла, выделенного в результате химической реакции.

Определите энтальпию процесса конденсации воды. Рассчитайте, сколько тепла выделится при образовании 1 м³ жидкой воды из пара при стандартных состояниях вещества.

Решение. Конденсация – это процесс перехода из газообразного состояния в жидкое, который относится к фазовым превращениям. Запишем уравнение конденсации для воды:

Н₂О(г) = Н₂О(ж).

Энтальпию этого превращения рассчитываем по следствию из закона Гесса, используя данные табл. (Приложение 2, [1]):

Δ_rН⁰₂₉₈= ∑ν_iΔ_f Н⁰_{298, продуктов} − ∑ν_jΔ_f Н ⁰_{298, исх веществ} ;

∆_rН⁰₂₉₈ = ∆_fН⁰_298Н2Ож – ∆_fН⁰_298Н2Ог = −285,84 – (−241,84) = −44 кДж.

Так как Δ_rН⁰₂₉₈ < 0, процесс конденсации экзотермический.

Энтальпии химической реакции Δ_rН равна тепловому эффекту этого процесса, протекающего в изобарно-изотермических условиях (Q_p,T):

Q_p,T = - Δ_rH_Т.

Определим количество вещества Н₂О, содержащееся в 1 м³. Так как плотность воды ρ = 1 г/см³, то масса 1м³ воды: m = ρV = 1·10⁶ г.

Количество молей Н₂О ν_Н2О = m/M_Н2О = 10⁶/18 = 5,56·10⁴ моль.

Поскольку при конденсации 1 моля воды выделяется 44 кДж тепла, то при конденсации 5,56·10⁴ молей выделится

Q = 44·5,56·10⁴ = 2,45·10⁶ кДж тепла.

Пример 7.Расчет удельной теплоты сгорания газового топлива.

Вычислить удельную теплоту сгорания газового топлива, содержащего 60% Н₂ и 40% СН₄, если известны теплоты сгорания газов: 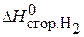= –286 кДж/моль; 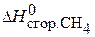= –890 кДж/моль.

Решение. Термохимические уравнения процессов сгорания водорода и метана:

Н_2(г) + ½О_2(г) → Н₂О_(ж); 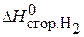= –286 кДж/моль;

СН_4(г) + 2О_2(г) → СО_2(г) + 2Н₂О_(ж) ; 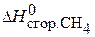= –890 кДж/моль.

Теплота сгорания топлива может быть рассчитана по следствию из закона Гесса:

Δ_rН⁰_Т = ∑ν_iΔ_fН_i⁰ _{продуктов} − ∑ν_jΔ_fН_j ⁰_{исх веществ} .

Удельная теплота сгорания газа Q_Т равна количеству теплоты, выделяющейся при сгорании 1м³ газообразного вещества до образования высших оксидов.

По условию задачи 1м³ данного газового топлива содержит 600 л Н₂ и 400 л СН₄, что составляет соответственно 600/22,4 молей Н₂ и 400/22,4 молей СН₄. (использовали молярный объем газа при нормальных условиях 22,4 л/моль).

В соответствии с уравнением:

Q_т = –DН_сгор×(1000/22,4),

рассчитаем удельную теплоту сгорания газового топлива:

Q_т = 286×(600/22,4) + 890×(400/22,4) = 7660,7 + 15892,8 = 23550 кДж/м³.

П 6. Расчет энтропии химической реакции. Расчет энергии Гиббса.

Определение термодинамической возможности самопроизвольного протекания химической реакции в заданном направлении. Определение температурной области самопроизвольного протекания химической реакции.

Пример 1.Расчет стандартной энтропии химической реакции при различных температурах.

Рассчитайте стандартную энтропию химической реакции

С(к) + СО₂(г) = 2СО(г)

при 298 К и при 1000 К, считая постоянными теплоемкости компонентов в рассматриваемом температурном интервале.

Решение. Энтропия S – функция состояния системы, которая служит мерой неупорядоченности этой системы, измеряется в Дж/(моль·К).

Согласно данным табл. (см. Приложение IV, [2]; Приложение 4, [3] ):

Вещество _f S⁰₂₉₈, Дж/(моль·K) С⁰_р298, Дж/(моль·К)

С(графит) 5,74 8,54

СО₂ (г) 213,68 37,41

СО (г) 197,54 29,14

Стандартная энтропия химической реакции при с.с. ( 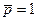и 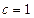моль/л) и 298 К, обозначается ∆_rS⁰₂₉₈ и рассчитывается по уравнению (следствие из закона Гесса):

Δ_rS⁰₂₉₈ = ∑ν_{i f}S⁰_{298,i продуктов} − ∑ν_{j f}S⁰_{298,j исх. веществ} ,

где _f S⁰₂₉₈ - стандартная энтропия образования веществ при 298 К (см. Приложение IV, [2]; Приложение 4, [3] ); ν_i - стехиометрические коэффициенты уравнения химической реакции.

Рассчитаем:

Δ_rS⁰₂₉₈ = 2S⁰_298,СОг − S⁰_298,Ск − S⁰_298,СО2г = 2(197,54) – 5,74 – 213,68 =

= 175,66 Дж/K.

То есть данная реакция при 298 К идет с увеличением энтропии, что и следовало ожидать, так как число молей газообразных веществ в результате реакции увеличивается.

Зависимость энтропии реакции от температуры в области 298 ÷Т, в которой нет фазовых переходов, в интегральном виде выражается уравнением

_Т

∆_rS⁰_T = ∆_rS⁰₂₉₈ + ∫ (∆_rС⁰_p/Т)dT ,

²⁹⁸

где ∆_rS⁰₂₉₈ − стандартная энтропия реакции при 298 К; ∆_rС⁰_p − изменение суммарной стандартной теплоемкости системы в ходе реакции.

Рассчитаем изменение стандартной теплоемкости системы в результате реакции:

∆_r С⁰ _р= 2С⁰_{р 298СОг} – С⁰_{р 298Ск} – С⁰_{р 298СО2г} = 2^.(29,14)–8,54–37,41 =12,33 Дж/К.

Для многих реакций можно пренебречь зависимостью С_р реагирующих веществ от Т, то есть ∆_rС⁰_p = const. Тогда имеем приближение в виде:

∆_rS⁰_T = ∆_rS⁰₂₉₈ + ∆_rС⁰_р(lnТ − ln298).

По этому уравнению рассчитаем

∆_rS⁰₁₀₀₀ = 175,66 + 12,33ln(1000/298) = 175,66 + 14,93 = 190,59 Дж/К.

Как следует из расчетов, увеличение энтропии реакции, обусловленное ростом суммарной теплоемкости системы, при изменении температуры на 702 К составляет около 8,5%.

Пример 2. Расчет энергии Гиббса химической реакции при стандартном состоянии и различных температурах. Возможное направление самопроизвольного протекания процесса.

Рассчитайте стандартную энергию Гиббса химической реакции

С(к) + СО₂(г) = 2СО(г)

при 298 К и при 1000 К. Сделайте вывод о возможности самопроизвольного протекания этой реакции при указанных температурах и стандартных состояниях всех компонентов.

Решение.Направление любого процесса определяется соотношением энтальпийного ∆_rН и энтропийного Т∆_rS факторов реакции.

Энергия Гиббса,или свободная энергия G - функция состояния системы, учитывающая совместное влияние этих факторов, G = H – TS.

Однозначный критерий возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях:

∆_rG_Т = (∆_rH_Т – T∆_rS_Т) < 0 .

1). Для начала, будем считать, чтоэнтальпия и энтропия реакции не зависят от температуры. В широком интервале температур в первом приближении можно считать неизменной величину стандартной теплоемкости веществ в ходе химической реакции ∆_rС⁰_p = 0 , тогда

∆_rН⁰_T = ∆_rН⁰₂₉₈ и ∆_rS⁰_T = ∆_rS⁰₂₉₈ .

Для расчета применим приближенную формулу расчета энергии Гиббса

∆_rG⁰_Т = ∆_rH⁰₂₉₈ − T∆_rS⁰₂₉₈ .

Используем данные, полученные в Примере 1. ( Δ_rS⁰₂₉₈ = 175,66 Дж/K) и в Примере 5. предыдущего практического занятия (Δ_rН⁰₂₉₈ = 172,5 кДж).

∆_rG⁰₂₉₈ = 172,5 – 298·175,66·10⁻³ = 120,15 кДж, то есть ∆_rG⁰₂₉₈> 0;

∆_rG⁰₁₀₀₀ = 172,5 – 1000·175,66·10⁻³ = −3,16 кДж, то есть ∆_rG⁰₁₀₀₀< 0.

Таким образом, при 298 К и стандартных состояниях веществ самопроизвольное протекание указанной реакции в прямом направлении невозможно (энтальпийный фактор не способствует самопроизвольному протеканию прямой реакции и определяет знак энергии Гиббса реакции при низких температурах). При высоких температурах определяющим становится энтропийный фактор реакции, он определяет отрицательное значение энергии Гиббса реакции при 1000 К и, следовательно, возможность самопроизвольного протекания реакции при этой температуре и стандартных состояниях компонентов.

2). Для более точного расчета ∆_rG⁰₁₀₀₀сначала рассчитаем изменение стандартной теплоемкости системы в ходе реакции:

∆_r С⁰ _р= 2С⁰_{р 298СОг} – С⁰_{р 298Ск} – С⁰_{р 298СО2г} = 2^.(29,14)–8,54–37,41 =12,33 Дж/К.

Значение стандартной ∆_rG⁰_Т для любой температуры Т можно в общем случае рассчитать с использованием справочных данных по уравнению:

_{Т Т}

∆_rG⁰_Т = ∆_rH⁰_Т −T∆_rS⁰_Т = ∆_rH⁰₂₉₈ + ∫ ∆_rС⁰_pdT + Т∆_rS⁰₂₉₈ + Т ∫ (∆_rС⁰_p/T)dT .

^{298 298}

Для многих реакций можно пренебречь зависимостью С_р реагирующих веществ от Т, то есть ∆_rС⁰_p = const. Тогда имеем приближение в виде:

∆_rG⁰_T = ∆_rG⁰₂₉₈ + ∆_rС⁰_р(Т − 298) - T^. ∆_rС⁰_р(lnТ − ln298).

Для расчета ∆_rG⁰₁₀₀₀используем это приближение:

∆_rG⁰₁₀₀₀= ∆_rG⁰₂₉₈ + ∆_rС⁰_р(Т − 298) - T^. ∆_rС⁰_р(lnТ − ln298) =

= 120150 +12,33^. (1000-298) – 1000^.12,33(ln1000 − ln298) =

= -9430 Дж = -9,43 кДж, то есть ∆_rG⁰₁₀₀₀< 0.

Как видно, имеется различие в значениях стандартной энергии Гиббса ∆_rG⁰_T, рассчитанной по разным методикам.

Пример 3. Определение температурной области самопроизвольного протекания реакции.

Определите температурную область самопроизвольного протекания реакции

С(к) + СО₂(г) = 2СО(г)

при стандартных состояниях компонентов.

Решение. Реакция может протекать самопроизвольно при стандартных состояниях компонентов в определенной области температур, для которых ∆_rG⁰_Т < 0.Чтобы найти эту область температур нужно определить граничную температуру (температуру равновесия), при которой значение ∆_rG⁰_Т меняет знак, то есть необходимо решить неравенство относительно Т:

∆_rG⁰_Т = ∆_rH⁰₂₉₈ + ∫^Т₂₉₈∆_rС⁰_pdT + Т∆_rS⁰₂₉₈ + Т∫^Т₂₉₈(∆_rС⁰_p/T)dT < 0.

Если пренебречь зависимостью ∆_rH⁰ и ∆_rS⁰от температуры, то граничную температуру (температуру равновесия) можно определить из приближенного неравенства:

∆_rG⁰_Т = ∆_rH⁰₂₉₈ − T∆_rS⁰₂₉₈< 0.

Подставляя в это выражение значения Δ_rН⁰₂₉₈ = 172,5 кДж и

Δ_rS⁰₂₉₈ = 175,66 Дж/K, (см. Пример 3) , получаем:

∆_rG⁰_Т =(172,5 – Т·175,66·10⁻³) < 0.

Откуда Т > 982 К. Верхним пределом искомой температурной области является предел существования наименее устойчивого компонента реакции, который находится из справочных данных.

Вещество Температурный интервал, К