Расчет энтальпий и теплоемкостей

Как видно из приведенных уравнений, при тепловом расчете реактора необходимо обязательно знать энтальпии реакций, энтальпии фазовых переходов компонентов и теплоемкости компонентов.

Если отсутствует табличное значение, то энтальпию реакции можно определить по стандартным энтальпиям образования или сгорания компонентов в соответствии с законом Гесса. Для реакции

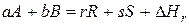
стандартная энтальпия реакции, рассчитанная по энтальпиям образования, равна

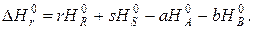
Соответственно по энтальпиям сгорания

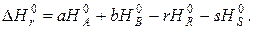
Значения стандартных энтальпий образования и сгорания можно найти в справочниках физико-химических величин. Значение энтальпии реакции при температуре реакции определяется уравнением

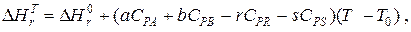
где С_Pi – мольная теплоемкость i-того компонента;

T₀– “стандартная” температура;

T– расчетная температура.

Энтальпии компонентов можно рассчитать, используя энтальпии фазовых переходов и температурные зависимости теплоемкостей фаз. При условии задания уровня отсчета T_cобщая формула при этом будет иметь вид

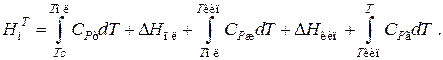
Индекс «пл» относится к температуре и энтальпии плавления, «кип» - к температуре и энтальпии кипения; «т», «ж» и «г» – соответственно к твердому телу, жидкости и газу. Температурные зависимости теплоемкостей для многих веществ можно найти в справочниках физико-химических величин, где они выражаются формулами:

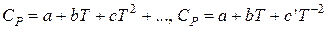
Если в данном температурном интервале в указанных уравнениях не окажется коэффициентов, то можно взять среднее значение теплоемкости, полученное из таблиц, или же рассчитанное по эмпирическим зависимостям.

Эмпирические зависимости расчета теплоемкости зависят от фазового состояния вещества. Так мольную теплоемкость металлов и других кристаллических веществ можно ориентировочно рассчитать по правилу Дюлонга и Пти, которое предполагает, что каждый атом соединения вносит в молекулу долю теплоемкости, равную примерно 26 Дж/(моль·К). Поэтому расчет удельной теплоемкости соединения можно провести по формуле

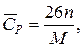
где n– число атомов в молекуле;

М – молекулярная масса соединения, кг/моль.

Теплоемкость многих твердых веществ – величина аддитивная и примерно равна сумме атомных теплоемкостей (правило Коппа):

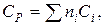
где n_i – число атомов данного вида;

С_i – атомная теплоемкость, выбираемая из таблицы 9.7.

Вопрос о расчете теплоемкости некристаллических твердых соединений пока еще не решен, хотя с достаточно высокой ошибкой ее можно определить по правилу Коппа.

Мольная теплоемкость идеальных газов при обычной температуре и давлении выражается соотношениями, приведенными в табл. 9.8).

Таблица 9.7. Атомные составляющие теплоемкости твердых веществ

Атом	Составляющая, Дж/(моль·К)	Атом	Составляющая, Дж/(моль·К)
C	7,53	F	20,92
H	9,62	P	23,0
O	16,74	Be	15,9
S	22,59	N	11,3
B	11,72	Другие атомы	25,92-26,78
Si	20,08

Таблица 9.8. Мольные теплоемкости идеальных газов

Вид газа	CV	CP	Вид газа	CV	CP
одноатомный	1,5R	2,5R	многоатомный	3R	4R
двухатомный	2,5R	3,5R

Здесь C_V и C_P – теплоемкости при постоянном объеме и постоянном давлении, соответственно, а R – универсальная газовая постоянная, равная 8,314 Дж/(моль·К).

Ориентировочное значение удельной теплоемкости в Дж/(кг·К) можно получить из следующих формул:

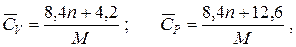
где n – число атомов в молекуле;

M –молярная масса соединения, кг/моль.

Зависимость теплоемкости газов и парогазовых смесей от давления и температуры ориентировочно определяется по формуле

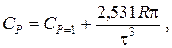
где C_P=1 – теплоемкость при атмосферном давлении, Дж/(моль·К);

p- приведенное избыточное давление газа,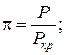

P – избыточное давление газа, Па;

P_кр – критическое давление газа, Па;

t - приведенная температура газа,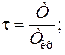

Т – температура газа, К;

Т_кр – критическая температура газа.

Теплоемкость газовых и парогазовых смесей можно приближенно определить из выражения

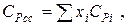
гдеx_i – молярная или объемная доля компонента в смеси.

Пример 9.7. Определить теплоемкость азота при температуре 50 ºС и абсолютном давлении 20 МПа.

Решение: По литературным данным для азота критическая температура равна 125,9 К, критическое давление – 3,285 МПа, молярная масса – 0,028 кг/моль. Определим изобарную теплоемкость при обычной температуре и атмосферном давлении

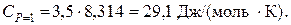
Приведенная температура равна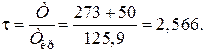

Приведенное избыточное давление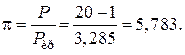

Тогда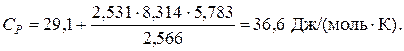

Или по удельной теплоемкости

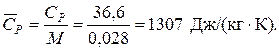
Удельная теплоемкость подавляющего большинства жидкостей лежит в пределах 1600-2400 Дж/(моль·К), для большинства углеводородов этот параметр примерно равен 2100 Дж/(моль·К).

Ориентировочную оценку мольной теплоемкости жидкостей можно провести, используя правило Коппа, которое применимо для температуры
20 ºС:

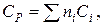
где n_i– число атомов данного вида;

C_i – атомная теплоемкость, выбираемая из табл. 9.9.

Мольную теплоемкость жидкостей при 20 ºС можно вычислить по методу Джонсона-Хуанга:

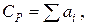
где a_i – атомная или групповая составляющие (см. табл. 9.9).

Таблица 9.9. Атомные составляющие теплоемкости жидкостей

Атом	Составляющая,Дж/(моль·К)	Атом	Составляющая,Дж/(моль·К)
C	11,72	Si	24,27
H	17,99	F	29,29
O	25,10	P	29,29
S	30,96	Другие атомы	33,5
B	19,66

Вторая формула Джонсона-Хуанга дает возможность получить температурную зависимость теплоемкости

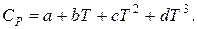
Коэффициенты a, b, c и d представлены в табл. 9.10.

Пример 9.8. Вычислить по методу Джонсона-Хуанга теплоемкость бензола (С₆Н₆) при 20 ºС.

Решение: Бензол можно представить состоящим из шести групп =СН¾, тогда С_Р=6·22,6=135,6 Дж/(моль·К). Опытное табличное значение 136,2 Дж/(моль·К).

Таблица 9.10. Атомные и групповые составляющие метода Джонсона-Хуанга

Атом, группа	ai, Дж/(моль·К)	Атом, группа	ai, Дж/(моль·К)
H (в муравьиной кислоте и ее эфирах)	14,86	¾CH=	46,05
¾CH3	41,44	¾NH2	63,63
¾CH2-	26,37	¾Cl	36,00
=CH¾	22,60	¾Br	15,49
¾COOH	79,95	¾NO2	64,05
¾COO— (сложные эфиры)	60,70	¾O— (простые эфиры)	35,16
>C=O	61,53	¾S¾	44,37
¾CºN	58,19	¾C6H5	127,67

Важной характеристикой при тепловом расчете реакторов может являться энтальпия испарения. В том случае, если нельзя найти ее табличное значение, ее можно рассчитать. Наиболее простым, но и не вполне точным методом является правило Трутона:

L_исп.к=87,9Т_к,

где L_исп.к– энтальпия испарения при температуре кипения, Дж/моль;

Т_к– температура кипения, К.

Таблица 9.11. Расчет теплоемкости по методу Джонсона-Хуанга

Группа	a	b·102	c·104	d·106
¾CH3	1.787	9.138	-0.3612	0.00465
¾CH2¾	-0.779	9.389	-0.5287	0.01147
=CH2	2.771	7.409	-0.3659	0.00699
=CH¾	-1.000	6.961	-0.4420	0.01088
C6H5¾	-31.71	46.08	-3.0516	0.07539
ºCH	8.443	5.860	-0.4843	0.01473
¾CH=	-21.987	16.27	-1.8418	0.06367
½ ¾CH ½	-8.129	11.85	-0.9548	0.02767
¾CH2—C6H5	-8.945	10.35	-0.5002	0.00829
¾CH2—C5H4	-9.703	10.34	-0.5417	0.01076
½ ¾C¾ ½	-19.49	15.41	-1.4865	0.04111
>C=	-0.224	5.618	-0.4266	0.01143

Более точным является метод Джиаколоне:

,

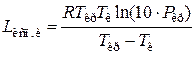где – Т_кр и Р_кр –критические температура (К) и давление (МПа).

Энтальпию плавления можно приближенно определить по формуле

L_пл=56,5Т_пл,

где L_пл – энтальпия плавления, Дж/моль;

Т_пл – температура плавления, К.

Для органических соединений соотношение между энтальпиями испарения и плавления имеет вид L_пл » 0,356L_исп.к.