Электрическая проводимость твердых тел

В идеальной решетке все ноны занимают свои места в узлах одинаково прочно, поэтому прохождение тока без разрушения решетки невозможно. Иное положение складывается, если кристаллическая решетка имеет дефекты. Ионы, расположенные на дефектных местах, а также по дислокациям, удерживаются в решетке менее прочно, чем остальные, и поэтому получают возможность двигаться под влиянием электрического поля. Дефекты в решетке могут приводить к нарушению нормального расположения ионов, но тем не менее решетка должна оставаться макроскопически нейтральной.

Прежде чем перейти к обсуждению возможных механизмов электрической проводимости, рассмотрим вопрос о природе переносчиков тока. Проверка с помощью закона Фарадея дает возможность установить наличие в твердых электролитах чисто ионной, смешанной электронно-ионной или только электронной проводимости. Показано, что большинству ионных кристаллов присуща чисто лонная проводимость или, во всяком случае, доля ионной проводимости столь велика, что электронной проводимостью можно пренебречь. Однако имеются твердые электролиты, которые обладают смешанной проводимостью, причем в зависимости от температуры доля электронной проводимости изменяется в широких пределах — от нуля до единицы (табл. 5.1). С повышением температуры в одних соединениях электронная проводимость заменяется ионной, а в других, наоборот, ионная — электронной.

Таблица 5.1. Доля электронной проводимости в твердых электролитах CuCl и γ-СuВг

Температура, ºС	Доля электронной проводимости		Температура, ºС	Доля электронной проводимости
CuCl	γ-CuBr	CuCl	γ-CuBr
	1,00 0,97 0,50	1,00 – 0,86			0,02 0,00 –	0,13 – 0,00

Определение характера проводимости (ионная или электронная) не решает еще полностью вопроса о механизме процесса, ибо

Таблица 5.2. Числа переноса ионов в некоторых соединениях

Вещество	Темпера-тура, ºС	Число переноса		Вещество	Темпера-тура, ºС	Число переноса
катиона	аниона	катиона	аниона
NaF NaCl   KCl   KBr		1,00 0,98 0,88 0,96 0,88 0,50 0,40	0,00 0,02 0,12 0,04 0,12 0,50 0,60		KI BaF2 BaCl2 CuI AgCl AgBr AgI	400–700 400–500 350–20 300–20 400–200	0,90 0,00 0,00 1,00 1,00 1,00 1,00	0,10 1,00 1,00 0,00 0,00 0,00 0,00

остается невыясненным при наличии ионной проводимости, какой сорт ионов участвует в переносе тока. Ответ могут дать, опыты по определению чисел переноса. Так, Тубандт установил, что иодид серебра обладает униполярной катионной проводимостью, а хло рид ртути в интервале 200 – 450 °С — униполярной анионной проводимостью.

Таблица 5.3. Числа переноса в кристаллическом хлориде натрия и иодиде свинца

Температура, ºС	Числа переноса в NaCl	Температура, ºС	Числа переноса в PbI2
t+	t–	t+	t–
	1.00 0.98 0.95 0.93	0.00 0.02 0.05 0.07		0.39 0.45 0.67	0.61 0.55 0.33

Униполярная анионная или катионная проводимость встречается в ионных кристаллах довольно часто (табл. 5.2). Однако

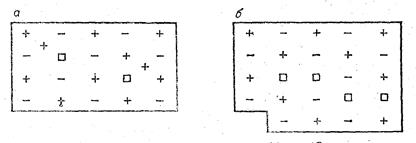
Рис. 5.2. Схема образования дефектов по Френкелю (а) и Шоттки (б),

в некоторых солях наблюдается биполярная проводимость, причем числа переноса аниона и катиона изменяются с температурой (табл. 5.3). Характер их изменения с температурой может быть различным, например с повышением температуры число переноса катиона в хлориде натрия уменьшается, а в иодиде свинца, наоборот, возрастает.

Выше отмечено, что проводимость ионных кристаллов определяется дефектами кристаллической решетки. Различают два типа дефектов. Одни дефекты связаны с тем, что некоторые ноны, благодаря флуктуациям тепловой энергии или каким-нибудь другим воздействиям (например, радиации), покидают свое нормальное место в узле кристаллической решетки и переходят в междуузлие + (рис. 5.2). В узле решетки появляется свободное место – вакансия □. Междуузельные ионы обычно бывают одного знака, причем знак ионов определяется размерами ионов и прочностью катионной и анионной подрешеток. Этот тип дефектов впервые рассмотрен Я. И. Френкелем и называется «дефектами Френкеля» или «дефектами по Френкелю».

Междуузельные ионы, опять-таки благодаря флуктуациям энергии, могут перескакивать из междуузлия в междуузлие, меняя свое местоположение. Следовательно, междуузельные ионы подвижны, но их движение беспорядочно, ненаправленно. В результате беспорядочного движения междуузельные ионы могут приблизиться к вакансии и в один из перескоков занять нормальное место в свободном узле решетки. При этом происходит одновременное исчезновение междуузельного иона и вакансии (рекомбинация).

Другой тип дефектов предложен В. Шоттки и носит название «дефектов Шоттки» («дефектов по Шоттки»). Эти дефекты образуются, когда, благодаря тепловым флуктуациям, ионы в узлах решетки выдавливаются на поверхность, образуя вакансии. При этом одновременно выдавливаются и положительно и отрицательно заряженные ионы. Суммарный электрический заряд всех выдавленных ионов равен нулю. Образование дефектов по Шоттки приводит к увеличению объема кристалла на объем образовавшихся вакансий (см. рис. 5.2).

Вакансии, так же как и междуузельные ионы, подвижны благодаря тому, что происходят перескоки ионов из узла решетки на

соседнюю вакансию; Если, скажем, произошел перескок иона из узла в вакансию слева направо, то это эквивалентно движению вакансии справа налево на такое же расстояние.

Если к кристаллу с дефектами приложить разность потенциалов, то движение междуузельных ионов, а также и вакансий становится направленным, ибо вероятность перескока в направлении поля становится больше, чем против поля. Следовательно, через кристалл начнет проходить ток, пропорциональный разности вероятностей перескока ионов или вакансий в разных направлениях.

В кристалле с дефектами Френкеля движение электрических зарядов может происходить либо путем перескока междуузельных ионов из одного междуузлия в другое (механизм Я. И. Френкеля), либо путем вытеснения междуузельным ионом нормального иона в следующее междуузлие (механизм Вагнера).

При наличии в кристалле дефектов Шоттки ионы под влиянием электрического поля начинают перескакивать из нормального положения в узле решетки в вакансию, вызывая тем самым как бы движение вакансий в обратном направлении. Когда подвижны ионы только одного знака, то происходит движение только вакансий того же знака, причем, если положительные или отрицательные ионы двигаются к. электроду противоположного знака, то вакансии двигаются к одноименному по знаку электроду.

В общем случае биполярной проводимости удельная электрическая проводимость кристалла будет равна сумме удельных электрических проводимостей, определяемых движением положительных и отрицательных ионов, т. е.

κ = κ₊ + κ_–

Но κ₊ и соответственно κ_– равны I₊ и I_– при градиенте потенциала, равном единице. В свою очередь ток пропорционален заряду «двигающихся единиц» (дефектов решетки), их числу в единице объема ( 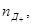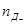) и абсолютной скорости дефектов ( 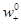и )

;

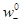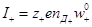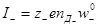
Следовательно

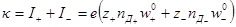
При униполярной проводимости формула для электрической проводимости упрощается

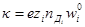
(индексом iобозначен сорт частиц, обеспечивающих электрическую проводимость).

Я. И. Френкель для определения числа дефектов применил формулу Больцмана

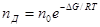
где n₀ — общее число ионов одного знака в единице объема; ΔG — изменение энергии Гиббса, необходимой для перевода одного моля

иона из нормального состояния в узлах кристаллической решетки в междуузлия (для дефектов по Френкелю) или же для образования одного моля вакансий одного знака (для дефектов по Шотт-ки). Так как энергии образования междуузельных ионов и вакансий различны, то ΔG нужно записывать с индексом, указывающим, к какому типу дефектов относится эта величина (ΔG_Ф и ΔG_Ш). В случае дефектов Френкеля выражение для удельной электрической проводимости получается в виде:

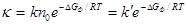
Константы k’и ΔG_Ф будут зависеть также от того, происходит ли междуузельный перескок ионов непосредственно или в соответствии с механизмом Вагнера.

Если же в кристалле имеются дефекты Шоттки, то

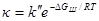
Известно, что ΔG = ΔH – TΔS, где ΔH — изменение энтальпии; ΔS — изменение энтропии процесса. Поэтому

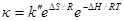
или, объединяя энтропийный член с константой, получаем:

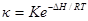
Оба варианта формулы Френкеля дают экспоненциальную зависимость удельной электрической проводимости ионного кристалла от температуры. После логарифмирования формулы Френкеля получаем:

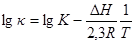
Из этого выражения следует, что температурная зависимость удельной электрической проводимости в координатах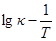

должна выражаться прямой линией, из угла наклона которой определяется ΔH

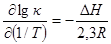
В формуле Френкеля константа

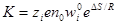
принята независимой от температуры. Между тем абсолютная скорость дефектов, безусловно, зависит от температуры. Если считать, что применимо уравнение Нернста — Эйнштейна, связывающее абсолютную скорость с коэффициентом диффузии D и температурой Т

w⁰ = DeN / RT

то

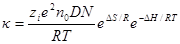и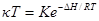

После логарифмирования получим

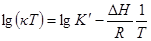
т. е. прямая линия должна лучше получаться в координатах lg (κT) — 1/T, чем в координатах lg κ — 1/T. Правда, часто обе формулы дают одинаково хорошие линейные зависимости, благодаря тому, что в доступном для измерений, довольно узком температурном интервале логарифм температуры изменяется не очень значительно.

Формула Френкеля по сути дела относится скорее к идеальному, чем к реальному, случаю прохождения тока через твердый электролит, поскольку она не учитывает возникающих изменений во взаимодействии между ионами в решетке в результате образования междуузельных ионов или вакансий.

Образование междуузелыюго иона, равно как и вакансии, должно вызвать вблизи от них искажение кристаллической решетки (рис. 5.3, а и б), в результате чего в формулу следовало бы ввести поправку на активность дефектов решетки хотя бы в виде коэффициента активности, аналогичного теории Дебая и Хюккеля.

Кроме дефектов Френкеля и Шоттки в кристаллических решетках всегда имеются искажения, связанные с наличием примесей. Если катионы или анионы примесей имеют отличные от основных ионов размеры или заряд, то замещение в узлах кристаллической решетки примесными ионами основных ионов неизбежно вызовет искажение решетки вокруг этих ионов, что увеличит подвижность ионов и приведет к росту удельной электрической проводимости. Такой тип проводимости называется примесной электрической проводимостью. Примесная электрическая проводимость сказывается обычно при низких температурах, когда собственная электрическая проводимость еще невелика. При повышении температуры собственная проводимость растет быстрее примесной и, начиная с некоторой температуры, роль примесной проводимости становится уже пренебрежимо малой. Естественно, что чем чище кристалл, тем меньше вклад примесной проводимости. Значение примесной проводимости обычно плохо воспроизводимо, так как искажения решетки определяются не только количеством примеси, но и ее распределением в основном компоненте. Последнее может определяться

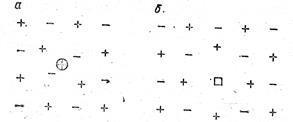
Рис. 5.3. Искажение расположения ионов в ближайшем окружении междуузельного иона (а) или вакансии (б).

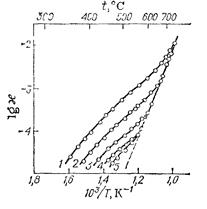
Рис. 5.4. Изменение с температурой электрической проводимости чистого хлорида калия и в присутствии добавок ВаС1₂.

Количество ВаС1₂, кмоль/м³: 1 –9∙10^–5; 2 – 3∙10^–5; 3 – 1,25∙10^–5; 4 и 5 – 0.

условиями кристаллизации. Следовательно, искажения решетки и удельная электрическая проводимость будут в определенных пределах изменяться от образца к образцу. Поэтому примесная проводимость является структурно-чувствительным фактором.

Приведенные на рис. 5.4 зависимости изменения удельной элек-трической проводимости КС1 с температурой, наглядно подтверждают сказанное. Так, зависимость lg κ – 10³/T для кристалла КС1 максимальной чистоты прямолинейна почти, во всем интервале температур, в котором возможно измерение. Только при самых низких температурах наблюдаются отклонения от прямолинейной зависимости, причем для двух образцов кристалла эти отклонения различны (сказываются структурно-чувствительные факторы).

Наличие в кристаллах хлорида калия ВаС1₂ нарушает прямолинейную зависимость тем больше, чем выше содержание примеси, а при 9∙10^–5 кмоль/м³ ВаС1₂ примесной проводимостью вообще уже нельзя пренебречь, даже при самой высокой температуре.

Электрическая проводимость ионных кристаллов с дефектами Френкеля или Шоттки, а также содержащих малые количества примесей, невелика и не превышает даже при высоких температурах 10^–1 См/м.

Имеется, однако, класс веществ, обладающих удельной электрической проводимостью, на несколько порядков превышающей удельную электрическую проводимость обычных ионных кристаллов. Их проводимость при комнатной температуре приближается к проводимости хорошо проводящих ток водных растворов. Такие твердые электролиты, называемые иногда ионными сверхпроводниками, характеризуются структурной разупорядоченностью одной из подрешеток, ионы которой оказываются весьма подвижными. Структурная разупорядоченность подрешетки может проявиться при кристаллизации как чистого соединения, так и соединения со значительной концентрацией примеси, стабилизирующей разупоря-доченную структуру.

К числу простейших ионных сверхпроводников относится высокотемпературная α-модификация иодида серебра, устойчивая в интервале температур от 147 °С до температуры плавления (555 °С) и обладающая разупорядоченной катионной подрешеткой. Низкотемпературные модификации β- и γ-AgI обладают значи-

тельно меньшей электрической проводимостью. Аналогично в соединении RbAg₄I₅ разупорядоченной является подрешетка ионов серебра. Остов соединения составляет подрешетка ионов иода. При температуре ниже –65 °С структура RbAg₄I₅ становится упорядоченной, и электрическая проводимость скачком уменьшается. Выше –65 °С и до температуры плавления (232 °С) существует высокотемпературная модификация с очень высокой электрической проводимостью.

Имеются и другие соединения с разупорядоченной структурой одной из подрешеток, обладающие высокой электрической проводимостью (KAg₄I₅; [(CH₃)₄]₂Ag₃I₅; Li₂SO₄ и др.).

Принято считать, что высокая электрическая проводимость такого рода соединений обусловлена наличием зигзагообразных каналов по местам разупорядоченных ионов. Эти каналы пронизывают всю толщу твердого электролита и по ним без больших трудностей двигаются ионы — переносчики заряда.

К числу твердых электролитов с разупорядоченной структурой одной из подрешеток, вызванной инородной добавкой, относятся, в первую очередь, электролиты на основе диоксида циркония. Чистый ZrO₂ при температурах до 1100 °С обладает небольшой электронной проводимостью. Выше 1100 °С ZrO₂ претерпевает превращение. Моноклинная структура превращается в тетрагональную. Появляется электронно-ионная проводимость, но величина ее остается небольшой. Если к ZrO₂ добавить, скажем, оксид кальция и спечь смесь при температуре около 1100 °С, то образуется кристаллическая структура флюорита; Катионные места решетки занимают вперемежку ионы Zr⁴⁺ и Са²⁺. Ввиду разности разрядов этих ионов, нехватка положительных зарядов компенсируется появлением вакантных узлов в анионной подрешетке. По вакантным узлам и начинают двигаться анионы кислорода, обеспечивая высокую электрическую проводимость. Такого типа структура проводника ZrO₂—CaO устойчива при содержании СаО порядка 10%.

Вместо СаО в качестве стабилизатора структуры можно применять оксиды MgO, Sc₂O₃, Y₂O₃, Nd₂O₃ и др. Известны и .другие твердые ионные сверхпроводники со стабилизирующими добавками, например: НfO₂—СаО (MgO, Y₂O₃); CeO₂—CaO (MgO, BaO); Y₂O₃—CaO и т. д.

Стекла в твердом состоянии являются аморфными, и их рассматривают как переохлажденные жидкости. В них нет дальнего порядка, т. е. обычной кристаллической структуры, но сохраняется ближний порядок. Электрическая проводимость стекол невелика и возрастает с температурой. Силикатные стекла обладают униполярной катионной проводимостью; это связано с тем, что в стеклах ионы SiO₃^2– образуют неподвижный анионный остов, а катионы, находящиеся между ними, более подвижны и. под влиянием разности потенциалов получают направленное движение.

Г. Т. Петровский и К. К. Евстропьев обнаружили в цезиевых фторбериллатных стеклах униполярную анионную проводимость, обусловленную переносом анионов фтора. Анионная униполярная проводимость наблюдается также в силикатных стеклах, содержащих некоторое количество галогенида натрия. В таких стеклах ток проводят ионы галогена.