Закон действующих масс. константы равновесия

В системе, состоящей из веществ, способных вступить в хими­ческое взаимодействие, реакция протекает при любых внешних условиях (т. е. при любой температуре и давлении). Однако скорость протекания реакции при этом может меняться от прак­тически незаметной до почти мгновенной.

Каждая химическая реакция при соответствующих условиях может протекать как в прямом направлении с образованием про­дуктов реакции, так и в обратном с превращением продуктов реакции в исходные вещества. Так, например, реакция 2SO + О_{2 ←}^→ 2СО₂ может протекать как в направлении образования углекислоты из окиси углерода и кислорода, указанном верхней стрелкой (прямая реакция), так и в обратном направлении разло­жения углекислоты 2СО₂ на кислород и окись углерода, указан­ном нижней стрелкой (обратная реакция).

При высокой начальной концентрации исходных веществ СО и О₂ прямая реакция протекает более интенсивно, при этом умень­шается количество исходных веществ и накапливаются продукты реакции — углекислота СО₂, которая, в свою очередь, начинает распадаться на составные части, превращаться в исходные ве­щества. Скорость этого превращения (интенсивность обратной реакции) увеличивается по мере накопления углекислоты СО₂. Эти два противоположных процесса при определенных условиях приводят термодинамическую систему в такое состояние, при котором сколько израсходуется в ней исходных веществ; столько же превратится в исходные вещества продуктов реакции, т. е. система будет находиться в химическом равновесии. Это равновесие называют кажущимся или динамическим (химические процессы в системе продолжают протекать). Момент установления динамического равновесия химической системы зависит от тем­пературы, давления и. концентрации реагирующих веществ.

Под скоростью химической реакции W подразумевается коли­чество вещества в киломолях, прореагировавшее в единице объема за единицу времени, т. е. изменение концентрации вещества в единицу времени:

W = -dC_i /dτ, (179)

где C_i — концентрация одного из исходных веществ, участвующих в реакции по формуле (5).

Скорость реакции всегда положительна. Знак минус в правой части ставится для того, чтобы скорость W_i была положительной, так как во время реакции концентрация исходных веществ умень­шается и, следовательно, имеет отрицательный знак.

На зависимость химического равновесия (для газообразных веществ) от давления и концентрации реагирующих веществ одним из первых обратил внимание русский ученый Н. Н. Бекетов (1865 T.). Он указывал, что химическое действие газов пропор­ционально давлению или массе и в зависимости от величины давле­ния химическое действие газов может совершаться даже и в об­ратном направлении, что это было подтверждено и показано в ма­тематической форме Гульдбергом и Вааге (1867 T.). Ранее Бертло (1801—1803 гг.) также указывал на зависимость направления химической реакции от концентрации реагирующих веществ для растворов.

Из курса общей химии известно, что скорость реакции соеди­нения двух идеальных газов прямо пропорциональна концентра­циям этих газов, т. е. при протекании реакции

2CO + O_{2 ←}^→ 2CO₂

скорость прямой реакции

W₁ = k₁C_COC_COCo₂ = k₁C²_COCo₂

Следовательно, скорость обратной реакции

W₂ = k₂C_COC_COCo₂ = k₂C²_Co₂,

где k₁ и k₂ — константы скорости соответственно прямой и обрат­ной реакции; С_CO , Со₂ и С_Со₂ — концентрации реагирующих газов.

Так как в состоянии химического равновесия

W₁ = W₂,

то можно записать

k₁C²_COCo₂ = k₂C²_Co₂, (180)

k₁/k₂ = K_C = C²_Co₂/ C²_COCo₂ (181)

где K_C — постоянная величина, выраженная через концентрации реагирующих газов (так называемая константа равновесия). Это уравнение (181) является выражением закона действующих масс. Такое уравнение выведено Гульдбергом и Вааге.

Выведем этот закон с использованием термодинамических и химических потенциалов (в частности, энергии Гиббса). Для этого рассмотрим обратимую реакцию в гомогенной газовой среде:

bВ + dD _←^→ еЕ + gG, (182)

где В, D, E, G —исходные вещества и продукты реакции, под­чиняющиеся законам идеального газа; b, d, e, g — стехиометрические коэффициенты.

Известно, что при равновесии сумма из произведения хими­ческого потенциала данного газа на бесконечно малое изменение его киломолей должна быть равна нулю.

Σ μ_i dn_i = 0.

Если обозначим химические потенциалы исходных веществ при равновесии через μ_B, μ_D, а полученных через μ_E и μ_G, то их алгебраическая сумма равна Σ μ_i dn_i и условие равновесия гомо­генной реакции можно записать в виде

eμ_E + gp_G — bμ_B — dμ_D = Σ μ_i dn_i = 0. (183)

Согласно уравнению (143) химический потенциал i-го компо­нента смеси идеальных газов

μ_i = μ_i(T) + RT ln p_i.

Найдем с помощью этого уравнения химические потенциалы исход­ных веществ и продуктов реакции:

eμ_E = eμ_E(T) + RT ln p^e_E;

gμ_G= gμ_G(T) + RT ln p^g_G;

bμ_B= bμ_B(T) + RT ln p^b_B;

dμ_D= dμ_D(T) + RT ln p^d_D;

Подставив полученные значения химических потенциалов в урав­нение (183), получим

eμ_E (Т) + gμ_G(T) - bμ_B(T) - dμ_D(T) + RT(ln p^e_E + ln p^g_G - ln p^b_B - ln p^d_D) = 0

После преобразований получаем

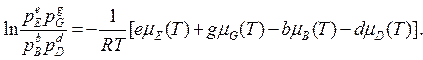(184)

Так как правая часть равенства представляет собой сумму ве­личин, зависящих лишь от температуры, то при каждой, выбран­ной для проведения реакции постоянной температуре эта вели­чина будет также постоянной. Обозначим ее In K_p, тогда равенство (184) можно переписать в виде

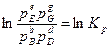(185)

и, следовательно,

K_p = 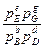(186)

где величина К_р является константой равновесия, выраженной через парциальные давления.

В соответствии с уравнением (184) величина К_р является функцией лишь температуры.

Найдем соотношения между константами равновесия, выра­женными через парциальные давления и концентрации.

Приняв число киломолей газов, участвующих в реакции (182), равными b = n_B d = n_D, e = n_Е и g = n_G, а объем, занимаемый газами V, можно, воспользовавшись уравнением Менделеева—Клапейрона (2), для каждого газа, взятого при одной и той же температуре Т (и учитывая, что С = n/V), написать значения парциальных давлений, выраженные чергез концен­трации:

Р_B = (n_B/V) RT = C_BRT и т. д.

Подставив парциальные давления в уравнение (186), получим

К_р = (C_ERT)^e (C_GRT)^g /(C_BRT)^b (C_DRT)^d = C^e_EC^g_G/C^b_BC^d_D(RT)^Δn. (187)

Полученная в формуле (187) величина C^e_EC^g_G/C^b_BC^d_D называется константой равновесия, выраженной через концентрации К_C , т. е.

K_C = C^e_EC^g_G/C^b_BC^d_D (188)

В уравнении (187) показатель степени Δn является изменением числа киломолей газов в ходе реакции; Δn = g + e —b —d. С учетом (188) уравнение (187) примет вид

K_p = K_c (RT)^Δn (189)

Следовательно,

K_c= K_p(RT)^-Δn. (190)

Из уравнений (188)—(190) видно, что в общем случае К_с ≠ К_р.

При Δn > 0 К_с < К_р, при Δn < 0 К_с > К_р. Чем выше тем­пература, тем больше отличаются К_с и К_р один от другого. Для реакций, в которых не происходит изменения числа киломолей (т. е. Δn = 0) К_с = К_р.

Соотношения, связывающие концентрации и парциальные давления в выражении констант равновесия К_с и К_Р, так же как и соотношения зависимости скорости химических реакций от концентрации реагирующих веществ, выражают закон действу­ющих масс. Из соотношений следует, что изменение концентрации (или парциального давления) одного вещества, участвующего в реакции, влечет за собой изменение концентраций (или пар­циальных давлений) остальных веществ. Причем изменение будет таким, что численное значение константы равновесия при данных условиях постоянно.

Для вывода уравнения константы равновесия применяются и другие термодинамические методы (Вант-Гоффа, Горстмана, Де-Донде и др.).

Численные значения константы равновесия, характеризующие состояние равновесия системы в данных условиях, всегда по­стоянны и не зависят от исходных концентраций реагирующих веществ, а также от того, какие из участвующих в реакции ве­щества принимаются за исходные и какие за продукты реакции, это можно проиллюстрировать на примере экспериментально хорошо изученной реакции образования йодистого водорода Н₂ + J₂ =2HJ. Здесь численные значения К_с и К_p совпадают, так как Δn = 0. Примем за исходные вещества Н₂ и J₂, т. е. предположим, что реакция в начальный момент идет в направле­нии образования HJ. Скорость ее зависит при этом от парциаль­ных давлений Н₂ и J₂; по мере образования йодистого водорода повышается его парциальное давление и возрастает скорость обратной реакции — реакции разложения HJ на водород и. иод. Если за исходное вещество принимается HJ, то в начальный момент разлагается HJ, скорость распада на составляющие за­висит от парциального давления йодистого водорода и по мере накопления продуктов распада Н₂ и J₂ скорость распада HJ уменьшается, а образование йодистого водорода из продуктов распада Н₂ и J₂ —увеличивается. Когда скорости прямой и об­ратной реакций станут равными, наступает химическое равновесие (рис. 32). В рассматриваемой химической системе через определен­ное время химическое равновесие наступает при одинаковых концентрациях независимо от того, какие исходные продукты рассматриваются (Н и J или HJ).

Экспериментально доказано, что равновесие достигается через 2 ч при 78% HJ и 11% Н₂ и J₂ при температуре 713 К. Этот равновесный состав для определенной температуры всегда постоян­ный. По известным концентрациям можно определить константу равновесия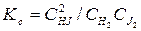

.

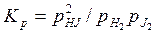При достижении равновесия системы энергия Гиббса G дости­гает минимального значения. При этом dG = 0. Рассматриваемая химическая реакция (рис. 33) будет протекать в направлении уменьшения энергии Гиббса G вплоть до достижения минималь­ного его значения (точка А). При этом dG = 0 и система нахо­дится в химическом равновесии.

При определении констант равновесия в уравнениях (188)— (190) для К_с и К_р в числителе принимаются концентрации и пар­циальные давления тех веществ, которые стоят в правой части, а в знаменателе — те, которые стоят в левой части стехиометри-ческого уравнения. Однако ранее в ряде учебников и учебных пособий в выражениях для определения констант равновесия концентрации и парциальные давления записывали в обратном порядке. Это обстоятельство следует иметь в виду, так как в этих случаях численные значения констант равновесия для одних и тех же реакций различны.

Константы равновесия К_с и К_р являются важными величинами для практических расчетов химических реакций. Зная константы равновесия, можно рассчитать состав продуктов сгорания и макси­мальную работу реакции. Константы равновесия определяют расчетным и экспериментальным путем. Для определенных тем­ператур и типа реакций полученные значения сведены в таблицы и приведены в соответствующих справочниках и учебниках.

Константы равновесия для газов, подчиняющихся уравнению Менделеева—Клапейрона, можно выразить и через число кило-молей веществ, участвующих в реакции,

K_n = n^e_E n^g_G/n^b_Bn^d_D

или через доли киломолей, равные по своей величине объемным долям r_i:

n_i/Σn_i = r_i ,

где r_i — объемная доля вещества в смеси

r_i = V_i/V; n_i — число киломолей вещества; Σn_i — сумма киломолей всех веществ в смеси.

Если воспользоваться соотношением между парциальными давлениями и киломольными долями, то можно найти соотношение между константами равновесия К_р, К_n и К_r.

Так как p_i = r_i р_см = (n_i/Σn_i) р_см , то, заменив парциаль­ные давления в уравнении (186), получим

К_p=(p^e_E p^g_G)/(p^b_B p^d_D)=r^e_Er^g_G 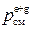/r^b_Br^d_D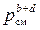

или, заменив отношение r^e_Er^g_G/r^b_Br^d_D на К_r , получим

Кр = K_r 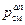(191)

Так как 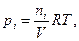, то

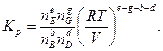
Заменив отношение n^e_E n^g_G/n^b_Bn^d_D на К_n, получим

K_p = K_n(RT/V)^Δn. (192)

Из полученных уравнений (189), (191) и (192) следует, что если в результате реакции изменяется число киломолей веществ, то численное значение констант равновесия различно, а соотно­шение между ними можно записать в виде

К_р = К_с (RT)^Δn = К_r 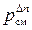=K_n (RT/V)^Δn (193)

Если в результате реакции число киломолей не изменяется, т. е. Δn = 0, то численное значение констант одинаково:

К_p = К_с = К_n = К_г. (194)

Для реальных газов константу равновесия можно выразить через фугитивность (летучесть) или активность, подставив в урав­нение (186) вместо парциальных давлений газов значения их фугитивностей. Тогда

K_f = f^e_Ef^g_G/f^b_Bf^d_D (195)

Чтобы выразить константу равновесия через активность а, в урав­нение (188) вместо концентраций газов надо подставить значения их активности, тогда

K_a = a^e_Ea^g_G/a^b_Ba^d_D. (196)

В табл. 5 приведены значения термодинамических констант равновесия К_а (196) для некоторых газовых реакций. Значений фугитивностей относятся к f₀; f₀ = 101 325 Па, a K_f = К_а