Конденсация Бозе–Эйнштейна

В газе из атомов бозонов часть атомов полностью теряет свою кинетическую энергию и импульс при достаточно низкой, но конечной температуре. Такие атомы называются бозе-конденсатом от лат. condenso – «сгущаю». Волновые функции атомов конденсата взаимно согласованы по фазе. На этой основе разработаны атомные лазеры, испускающие атомы с когерентными волновыми функциями.

Явление полной потери кинетической энергии у части идеального бозонного газа при низкой температуре теоретически открыл А. Эйнштейн в 1925 г. Процесс называется бозе-конденсацией частиц в импульсном пространстве. Его детально исследовали Фриц и Хайнц Лондоны в 1938 г. Бозе-конденсация является следствием того, что химический потенциал бозонного газа не может быть положительным. При нормальной температуре химический потенциал газа отрицательный. При уменьшении температуры химический потенциал увеличивается, и при достаточно низкой температуре достигает наибольшего возможного значения 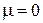. Дальнейшее понижение температуры вызывает уменьшение числа частиц в газовой фазе и часть атомов выпадает в конденсат.

Хайнц Лондон (1907–1970) и Фриц Лондон (1900–1954) –

основатель теории сверхпроводимости и квантовой химии

Получить конденсацию экспериментально не удавалось более 50 лет, поскольку при низкой температуре межатомное взаимодействие притягивает атомы друг к другу, образуются кластеры и далее жидкое или твердое состояние до начала бозе-конденсации. Кластер возникает при столкновении трех и более частиц, что вероятнее при высокой концентрации. При низкой концентрации частиц преобладают парные столкновения, обеспечивающие установление теплового равновесия. Для предотвращения образования кластеров нужно снижать концентрацию газа. Метастабильный бозе-конденсат в разреженных газах атомов рубидия, натрия, лития впервые получили В. Кеттерле, К. Виман и Э. Корнелл в 1995 г. Атомы водорода конденсированы в 1997 г. Бозе-конденсат проявляет уникальные свойства: температура 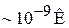, скорость света 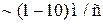, скорость звука .

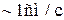Вольфганг Кеттерле, Карл Виман, Эрик Корнелл

Атомы бозоны. Спин атома складывается из спинов электронов оболочки и нуклонов ядра, их спины равны 1/2. Число электронов равно числу протонов, поэтому их общий спин в электрически нейтральном атоме целочисленный. Спин атома определяется числом нейтронов. Бозонами являются атомы с четным числом нейтронов, например: ₁H¹, ₂He⁴, ₃Li⁷, ₁₁Na²³, ₃₇Rb⁸⁷, где нижняя цифра – порядковый номер элемента в таблице Менделеева, или число протонов в ядре, верхняя цифра – массовое число, или число протонов и нейтронов в ядре. Атом с четной разностью цифр является бозоном. При сверхнизких температурах атомы находятся в основном состоянии, поэтому первые два имеют нулевой спин, а у последних трех спин равен единице. Число спиновых состояний

.

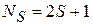Барионное число нуклонов сохраняется, поэтому число атомов в изолированной системе не изменяется.

Распределение бозонов по энергии. Используем распределение Бозе–Эйнштейна (4.10) для среднего числа частиц в одном состоянии

,

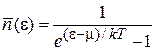и плотность состояний трехмерного газа (3.8)

, .

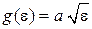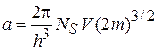Получаем число частиц в интервале энергии 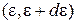в газе объемом V

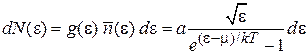. (4.77)

Полное число частиц находим из (4.77)

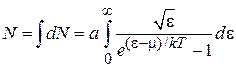. (4.78)

Химический потенциал определяется из (4.78). При изменении температуры число частиц сохраняется, тогда от T не зависит

,

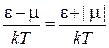где учтено 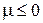. Следовательно, при уменьшении температуры уменьшается |m|, и химический потенциал увеличивается от отрицательных значений до нуля. Если 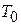– температура, при которой химический потенциал обращается в нуль:

,

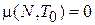тогда при 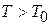выполняется

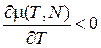. (4.79)

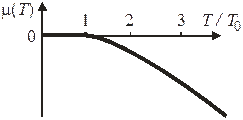
При понижении температуры ниже 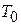рост μ невозможен, и (4.78) выполняется за счет уменьшения числа частиц газа .

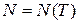Порог конденсации 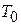– это верхняя граница интервала температуры 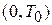, где химический потенциал равен нулю. Из (4.78) получаем

,

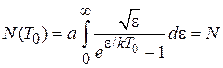где N – число частиц газа при нормальной температуре. Используя

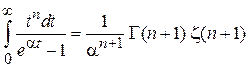
при 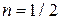, находим интеграл

,

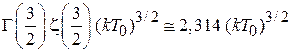получаем

,

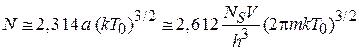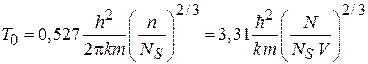. (4.80)

Температура порога конденсации возрастает с увеличением концентрации атомов 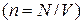и с уменьшением массы атома.

Массу атома выражаем через молярную массу

,

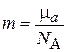концентрацию атомов выражаем через молярный объем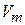

.

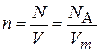Из (4.80) в системе единиц СГС получаем

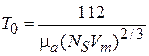[К]. (4.81)

Для ₂He⁴ с параметрами:

, , ,

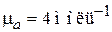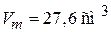находим

.

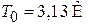Получим длину волны де Бройля при 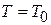. Для атома со средней энергией

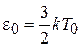
и импульсом

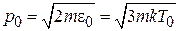
используем (4.80) и получаем

,

.

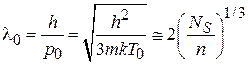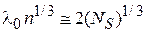Учитывая 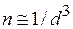, где d – среднее расстояние между атомами, находим

.

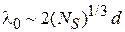При понижении температуры длина волны де Бройля атома увеличивается и при достижении порога конденсации сравнивается с расстоянием между атомами. Волновые функции частиц перекрываются, интерферируют и бозе-конденсат проявляет квантовые свойства.

Число конденсированных частиц. В интервале температур 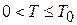химический потенциал равен нулю. При температуре ниже Т₀ уравнение (4.78)

, ,

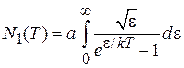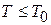выполняется за счет уменьшения числа частиц в газовой фазе от первоначального N до текущего N₁(Т). Аналогично (4.80) получаем

, .

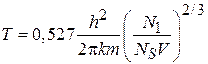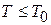Результат делим на (4.80)

,

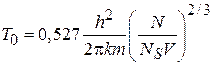и находим число и концентрацию частиц, оставшихся при 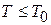в газовой фазе:

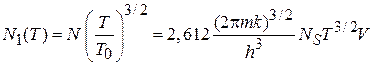, (4.82)

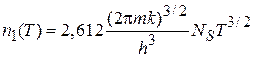. (4.82а)

Число конденсированных частиц

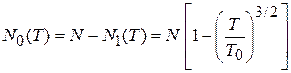. (4.83)

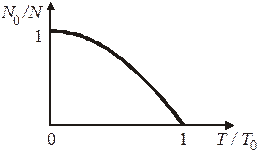
Относительное число конденсированных частиц показано на рисунке.

Внутренняя энергия и теплоемкость. Используя (4.77)

,

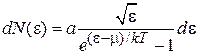получаем внутреннюю энергию

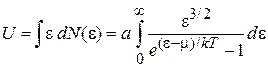, (4.84)

где .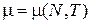

В области конденсации находим

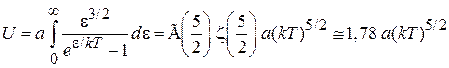
или

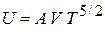, (4.85)

где

.

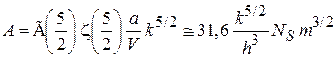Внутренняя энергия определяется вкладом лишь газовой фазы, внутренняя энергия конденсированной фазы равна нулю. Из (4.85) и (4.82)

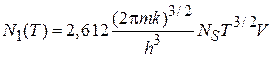
находим энергию, приходящуюся на частицу газовой фазы в области конденсации:

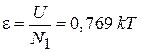. (4.86)

Из (4.85) находим теплоемкость ниже порога конденсации:

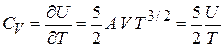. (4.87)

Учитывая (4.80)

,

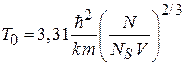из (4.87) получаем теплоемкость при температуре конденсации

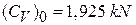. (4.87а)

Свободная энергия. Из (4.85)

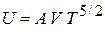
и из уравнения Гиббса–Гельмгольца (2.29) находим

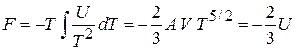. (4.88)

Энтропия и давление выражаются через свободную энергию

,

.

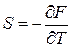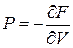С учетом (4.88) в области конденсации получаем

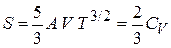, (4.89)

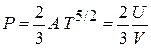, (4.90а)

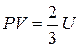. (4.90б)

Выражение (4.90б) является уравнением состояния нерелятивистского идеального квантового газа, и совпадает с уравнением состояния классического идеального газа. Сравнивая (4.89) и (4.82)

,

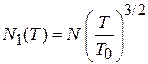находим, что энтропия пропорциональна числу частиц газовой фазы. Следовательно, энтропия конденсированной фазы равна нулю. Давление (4.90а) определяется температурой и не зависит от объема. Конденсированные частицы имеют нулевой импульс и не создают давления. Оно определяется концентрацией частиц газовой фазы (4.82а)

,

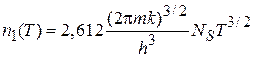тогда

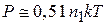. (4.91)

Осуществление конденсации. Двухчастичные столкновения обеспечивают термодинамическое равновесие газа. Трехчастичные столкновения приводят к образованию жидкого и твердого состояний. При относительно больших плотностях газа существенны трехчастичные столкновения. Межатомное взаимодействие образует жидкое или кристаллическое состояние при низких температурах. При малой плотности газа вероятность трехчастичных столкновений существенно меньше двухчастичных столкновений. В результате при низких температурах возможно газообразное метастабильное состояние с достаточно большим временем жизни. Первые конденсаты получены из атомов рубидия, натрия, водорода при температуре газовой фазы ~10^–2 К, под давлением P < 10^–11 мм рт. ст. с числом частиц ~10⁸ и концентрацией ~10¹⁴ см^–3.

Удержание газа в вакуумированной стеклянной ячейке в области размером менее 1 мм осуществляется магнитной ловушкой. Система катушек создает неоднородное магнитное поле с абсолютным минимумом в центре. Магнитный момент атомаp_m в магнитном поле B получает энергию (–p_m×B). Для точки 2 в центре ловушки поле пренебрежимо мало, для точки 1 в стороне от центра поле B сильное. При термодинамическом равновесии электрохимические потенциалы во всех точках одинаковые

.

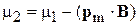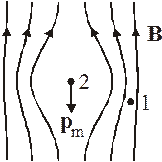
Магнитная ловушка

В основном состоянии атома ₂Не⁴ спины электронов направлены в противоположенные стороны, их магнитные моменты скомпенсированы и у атома нет собственного магнитного момента. При включении внешнего магнитного поля в атоме возникает круговой ток электронов благодаря явлению электромагнитной индукции. Согласно правилу Ленца, индуцированный магнитный момент направлен против внешнего поля, это дает

,

.

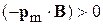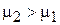Химический потенциал растет с увеличением концентрации частиц, тогда получаем

.

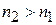Атомы с магнитными моментами, направленными против поля, выталкиваются из сильного в слабое магнитное поле – «диамагнитные атомы ищут слабое поле». В результате атомы собираются и удерживаются в центре ловушки. Область удержания имеет вид сигары диаметром ~(10…50) мкм, длиной ~300 мкм. Из ловушки атомы выводятся коротким импульсом высокочастотного излучения, наклоняющего магнитные моменты атомов. Возникает суперпозиция состояний с моментами, направленными против- и по полю, последнее состояние выталкивается ловушкой.

Для удержания бозе-конденсата также разработаны микросхемы, создающие необходимую конфигурацию магнитного поля на расстоянии ~0,1 мм от своей поверхности и потребляющие мощность ~1 Вт. На таких расстояниях чип создает более неоднородное магнитное поле, чем катушка, обеспечивая лучшее удержание газа. Чип миниатюрен, имеет комнатную температуру, его тепловое излучение слабо поглощается газом. Изменением токов чипа можно перемещать центр ловушки и двигать бозе-конденсат вдоль поверхности чипа.

Охлаждение газа осуществляется лазерным методом, основанным на эффекте Доплера. Если на хаотически движущиеся атомы направить лазерное излучение с частотой n < n₀, где n₀ – частота резонансного поглощения атома, то покоящиеся и движущиеся от лазера атомы не поглощают излучение. Атом, движущийся к лазеру со скоростью V, воспринимает частоту

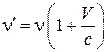
и при n¢ = n₀ поглощает фотон. В результате атом получает импульс против своей скорости и тормозится. Возбужденный атом излучает энергию в среднем изотропно. Излучение в близкой инфракрасной области спектра, созданное полупроводниковыми лазерами и направленное на газ с шести взаимно перпендикулярных сторон, приводит к его охлаждению.

Используется также испарительное охлаждение путем выбрасывания с периферии ловушки атомов, имеющих наибольшую скорость, при помощи высокочастотного магнитного поля. Оно наклоняет магнитные моменты, создает составляющую по направлению поля, которая выбрасывается ловушкой. Частицы с более высокой скоростью быстрее достигают границы газа и их концентрация у границы выше концентрации частиц с малой скоростью. Поэтому больше вероятность испарения высокоэнергичных частиц. Для ловушки на основе катушек происходит охлаждение до температуры газовой фазы порядка 10^–7 К за время от 10 с до 10 мин. Для чипа необходимая для конденсации температура достигается за время меньшее 1 с. Концентрация атомов конденсата составляет ~10¹⁴ см^–3, тепловая энергия соответствует температуре, меньшей 10^–11 К.

Атомный лазер. Частицы бозе-конденсата занимают нижний энергетический уровень, взаимно когерентны, описываются единой волновой функцией. Атомный лазер создает пучок когерентных атомов с единой волновой функцией

,

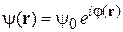с импульсом

,

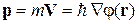с длиной волны де Бройля до 1 мм. Наблюдалась интерференция между частями конденсата, разрезанного лазерным лучом. При выключении магнитного поля ловушки части конденсата падают в вакууме, расширяются, накладываются друг на друга и интерферируют. В максимуме интерференции концентрация частиц увеличивается, в минимуме – уменьшается. Из атомов рубидия получен когерентный пучок с поперечным сечением до 1 нм. Это позволяет размещать атомы на подложке с высокой точностью. Получено усиление когерентной атомной волны, проходящей через конденсат, облучаемый оптическим лазером. Атомы конденсата присоединяются к пучку атомов, изменяя свой импульс путем рассеяния фотона. При этом они сохраняют фазовую когерентность пучка и увеличивают его интенсивость.

Изложенная теория бозе-конденсации не учитывала поля ловушки, в которой находится газ. Рассмотрим влияние внешнего поля на процесс конденсации, и аналогичные явления в системах пониженной размерности.

ТРЕХМЕРНЫЙ БОЗЕ-ГАЗ

В ПОТЕНЦИАЛЬНОЙ ЛОВУШКЕ

Нерелятивистский бозонный газ с числом частиц N удерживается ловушкой с потенциальной энергией

.

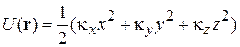Найдем температуру порога конденсации T_C.

Для системы в параболической ловушке ранее получена плотность состояний (П.8.2а)

,

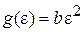где

, .

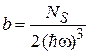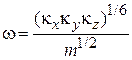Результат существенно отличается от рассмотренного ранее случая свободного газа с 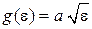, где 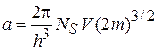. Для числа частиц получаем

,

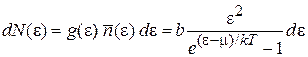При температуре порога конденсации T_C химический потенциал 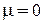, тогда число частиц системы

.

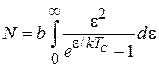Используем

,

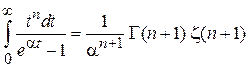при 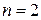вычисляем интеграл

,

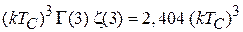получаем отличную от нуля температуру конденсации

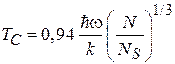. (П.13.4)

Сравниваем (П.13.4) с температурой конденсации свободного трехмерного газа (4.80)

.

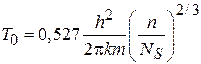Для частиц в ловушке температура конденсации растет медленнее с увеличением числа частиц по сравнению со свободным газом.

ВОЗМОЖНА ЛИ КОНДЕНСАЦИЯ