Модуль 1. Химическая термодинамика

Законы термодинамики и их применение к простейшим процессам. Первый закон термодинамики. Внутренняя энергия, энтальпия, теплота, работа. Работа и теплота как характеристики процесса. Взаимосвязь теплоты, работы и изменения внутренней энергии. Применение первого закона термодинамики к простейшим процессам. Тепловые эффекты и теплоты образования. Связь величины Q_р и Q_V. Закон Гесса и его термодинамическое обоснование. Теплоемкость вещества. Зависимость теплоемкости вещества от температуры. Зависимость тепловых эффектов процессов от температуры. Вывод и анализ уравнения Кирхгофа. Расчеты тепловых эффектов химических реакций, теплоты агрегатных и фазовых превращений, теплоты растворения при различных температурах.

Второй закон термодинамики. Самопроизвольные и несамопроизвольные процессы. Энтропия. Приведенная теплота и энтропия для равновесных и неравновесных процессов. Изменение энтропии как критерия равновесия и направления процессов в изолированной системе. Вычисление изменения энтропии при охлаждении (нагревании) веществ и при фазовых переходах.

Третий закон термодинамики. Формулировки третьего закона термодинамики и следствия. Постулат Планка. Вычисление абсолютных стандартных величин энтропии вещества по термодинамическим данным. Энергия Гиббса, энергия Гельмгольца, химический потенциал. Физический смысл этих величин. Применение энергии Гиббса и энергии Гельмгольца в качестве критериев направленности процессов и равновесия в изотермических системах. Зависимость энергии Гиббса от температуры и давления.

Химическое равновесие. Динамическая и термодинамическая характеристика равновесия. Термодинамический закон действия масс. Константа равновесия. Способы выражения константы равновесия в гомогенных и гетерогенных системах. Вычисление состава равновесной системы, выхода продукта, степени превращения исходных веществ, степени диссоциации. Уравнения изобары и изохоры химической реакции. Уравнение изотермы и направление химической реакции. Константа равновесия и стандартное изменение энергии Гиббса. Расчет изменения энергии Гиббса и констант равновесия для различных температур, приближенные методы расчета константы равновесия.

Задание 1.1. Определение тепловых эффектов химических реакций

Вычислите тепловой эффект образования вещества А из простых веществ при температуре 298 К и стандартном давлении, если известна его энтальпия сгорания при этой температуре и стандартном давлении (табл. 1). При вычислении следует принять, что конечные продукты сгорания СО_2(г), Н₂О_(ж), N_2(г).

Теплоты сгорания простых веществ указаны в следующих уравнениях:

С_{(графит)} + О_2(г) = СО_2(г) + 393,51 ;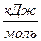

Н_2(г) + 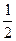О_2(г) = Н₂О_(ж) + 285,83 .

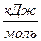Таблица 1

Номер варианта	Вещество А	Формула	Состояние	∆Нсгор,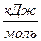
	Мочевина	СН4N2О	т	–632,20
	Нитрометан	СН3NО2	ж	–708,77
	Ацетальдегид	С2Н4О	г	–1193,07
	Этилацетат	С4Н8О2	ж	–2246,39
	Глицерин	С3Н8О3	ж	–1661,05
	Диметиламин	С2Н7N	ж	–1768,59
	Ацетон	С3Н6О	ж	–1785, 73
	Пентан	С5Н12	г	–3536,15
	Триметиламин	С3Н9N	г	–2442,92
	Пропанол-1	С3Н8О	ж	–2010,41
	Бутан	С4Н10	г	–2877,13
	Амиловый спирт	С5Н12О	ж	–3320,84
	Фенол	С6Н6О	т	–3063,52
	Гидрохинон	С6Н6О2	т	–2860,60
	Анилин	С6Н7N	ж	–3396,20
	Бензойная кислота	С7Н6О2	т	–3226,70
	Пиридин	С5Н5N	ж	–2755,16
	Стеариновая кислота	С18Н36О2	т	–11274,60
	Толуол	С7Н8	ж	–3947,94
	Октан	С8Н18	ж	–5470,58
	Нафталин	С10Н8	т	–5156,78
	Гексан	С6Н14	г	–4194,75
	Изобутан	С4Н10	г	–2868,76
	Сахароза	С12Н22О11	т	–5646,73
	Уксусная кислота	С2Н4О2	ж	–874,58
	Камфора	С10Н16О	т	–5924,84
	Бутанол	С4Н10О	ж	–2671,90
	Формальдегид	СН2О	г	–561,07
	Щавелевая кислота	С2Н2О4	т	–251,88
	Антрацен	С14Н10	т	–7067,45

Задание 1.2. Определение возможности протекания химической реакции в стандартных и нестандартных условиях

Выполните следующие девять заданий для данной реакции (табл. 2) (справочные величины, необходимые для расчетов, возьмите в прил. 1).

1. По значениям стандартных энтальпий образования участвующих в реакции веществ DH⁰_f,298, вычислите тепловой эффект реакции при стандартных условиях DH⁰₂₉₈. Выделяется или поглощается тепло при протекании реакции? Эндо - или экзотермической является данная реакция?

2. Для исходных веществ и продуктов реакции определите величины средних теплоемкостей 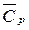в диапазоне температур 298 – Т и изменение теплоемкости Δ 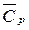в ходе реакции. Пользуясь законом Кирхгофа вычислите тепловой эффект реакции DH⁰_Т при температуре T и стандартном давлении с учетом величины Δ .

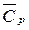3. Выведите для реакции функциональную зависимость изменения молярной изобарной теплоемкости от температуры: DC⁰_p = f(T).

4. Вычислите величину DH⁰_Т, пользуясь законом Кирхгофа и установленной функциональной зависимостью DC⁰_p = f (T). Как влияет увеличение температуры на величину теплового эффекта реакции?

5. Качественно оцените знак изменения энтропии DS при протекании реакции. Объясните полученный результат. По значениям стандартных энтропий участвующих в реакции веществ S⁰₂₉₈ вычислите изменение энтропии реакции при стандартных условиях DS⁰₂₉₈.

6. Используя функциональную зависимость DC⁰_P = f (T) вычислите изменение энтропии реакции DS⁰_T при температуре T и стандартном давлении. Как влияет повышение температуры на величину DS⁰_T?

7. Качественнооцените вероятность самопроизвольного протекания реакции при высоких и низких температурах. Вычислите изменение энергии Гиббса DG⁰₂₉₈ реакции, протекающей при стандартных условиях. Возможно ли самопроизвольное протекание процесса при стандартных условиях? Определите температуру T₀, при которой реакция меняет свое направление.

8. Вычислите изменение энергии Гиббса DG⁰_T реакции, протекающей при стандартном давлении и температуре T, считая, что DH⁰_T и DS⁰_T не зависят от температуры (метод Улиха). Постройте график зависимости DG⁰_T от температуры. Сделайте вывод о влиянии температуры на вероятность самопроизвольного протекания процесса в прямом направлении.

9. Вычислите изменение энергии Гиббса DG⁰_T реакции при температуре T и стандартном давлении, учитывая зависимость DH⁰_T и DS⁰_T от температуры. Сравните полученные значения DG⁰_T с величиной изменения энергии Гиббса, рассчитанной по методу Улиха, и оцените их расхождение.

Таблица 2

Номер варианта	Реакция	Т, К
	4NH3(г) + 5O2(г) = 4NO(г) + 6H2O(г)
	4HCl(г) + O2(г) = 2Cl2(г) + 2H2O(г)
	2KOH(т) + CO2(г) = K2CO3(т) + H2O(г)
	2NaHCO3(т) = Na2CO3(т) + H2O(г) + CO2(г)
	2CuS(т) + 3O2(г) = 2CuO(т) + 2SO2(г)
	Fe3O4(т) + 4H2(г) = 3Fe(т) + 4H2O(г)
	2H2S(г) + 3O2(г) = 2SO2(г) + 2H2O(г)
	Mg(OH)2(т) = MgO(т) + H2O(г)
	CS2(г) + 3O2(г) = CO2(г) + 2SO2(г)
	MgCO3(т) = MgO(т) + CO2(г)
	Fe2O3(т) + 3H2(г) = 2Fe(т) + 3H2O(г)
	Ca(OH)2(т) + CO2(г) = CaCO3(т) + H2O(г)
	BaO(т) + CO2(г) = BaCO3(т)
	4HBr(г) + O2(г) = 2Br2(г) + 2H2O(г)
	4NH3(г) + 3O2(г) = 2N2(г) + 6H2O(г)
	SnO2(т) + 2H2(г) = Sn(т) + 2H2O(г)
	4FeS2(т) + 11O2(г) = 2Fe2O3(т) + 8SO2(г)
	2H2S(г) + O2(г) = 2H2O(г) + S2(г)
	FeO(т) + H2(г) = Fe(т) + H­2O(г)
	CaO(т) + H2O(г) = Ca(OH)2(т)
	Al2O3(т) + 3SO3(г) = Al2(SO4)3(т)
	2NO(г) + O2(г) = 2NO2(г)
	2NiS(т) + 3O2(г) = 2NiO(т) + 2SO2(г)
	TiO2(т) + 2H2(г) = Ti(т) + 2H2O(г)
	PbO(т) + SO3(г) = PbSO4(т)
	4CO(г) + 2SO2(г) = 4CO2(г) + S2(г)
	CO(г) + H2O(г) = CO2(г) + H2(г)
	Fe2O3(т) + 3CO(г) = 2Fe(т) + 3CO2(г)
	SnO2(т) + 2CO(г) = Sn(т) + 2CO2(г)
	2ZnS(т) + 3O2(г) = 2ZnO(т) + 2SO2(г)

Задание 1.3. Химическое равновесие

Газообразные вещества А и Б реагируют с образованием газообразного вещества В (табл. 3).

Выполните следующие задания для данной реакции:

1. Выразите константы равновесия K_P и K_C через равновесное количество вещества В, равное x, если исходные вещества А и Б взяты в стехиометрических количествах при общем давлении в системе P и температуре T, К.

2. Рассчитайте K_P и K_C при 300 К, если Р = 7,5·10⁴ Па, x = 0,45.

3. Вычислите равновесное количество вещества С при давлении в системе, равном 3·10⁴ Па и температуре 300 К.

4. Рассчитайте степень превращения веществ А и Б при T = 300 К.

Таблица 3

Номер варианта	Уравнение реакции	Номер варианта	Уравнение реакции
	А + Б = 1/2В		3/2А + Б = 3/2В
	1/2А + Б = В		А + 3Б = 3В
	3А + Б = 2В		3А + Б = В
	2А + 3Б = 3В		А + 2Б = 2В
	2А + 1/2Б = 2В		2А + 2Б = 1/2В
	3А + 1/2Б = В		А + Б = В
	А + 2Б = В		2А + 2Б = В
	А + Б = 3В		2А + 2Б = 3В
	1/2А + Б = 2В		3А + 3Б = 2В
	1/2А + Б = 3В		1/2А + Б = 1/2В
	2А + 1/2Б = 3В		1/2А + 1/2Б = 2В
	2А + 3Б = 2В		А + Б = 3/2В
	3А + 1/2Б = 3В		2А + 2Б = 3/2В
	3А + 1/2Б = 2В		3/2А + 1/2Б = В
	1/2А + 1/2Б = 3В		3/2А + Б = 3/2В

Пример 1.1. Истинная молярная теплоемкость серебра в интервале температур от 273 до 1234 К выражается уравнением (см. прил. 1):

С⁰_P = 23,97 + 5,27×10^–3 Т – 0,25×10⁵ Т ^–2 .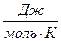

Вычислите среднюю молярную теплоемкость серебра 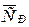в интервале от 298 до 700 К.

Решение. Среднюю теплоемкость в данном интервале температур рассчитывают по уравнению:

,

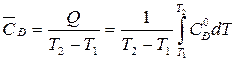где Q – количество теплоты, подведенной к системе.

С учетом зависимости истинной теплоемкости от температуры

С_P = а + bT + c^{1 .} T^–2

получим выражение:

.

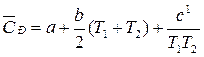Подставляя коэффициенты a, b, c¹ и температуру из условия задачи, получаем: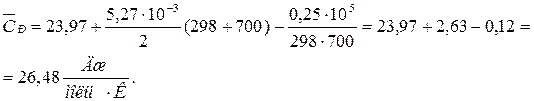

Пример 1.2.Определите энтальпию образования метана, если его энтальпия сгорания (DH⁰_сгор.) равна –890,31 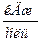. Значения энтальпий сгорания водорода и углерода возьмите из термохимических уравнений:

С_{(графит)} + О_2(г) = СО_2(г) + 393,51 ;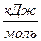

Н_2(г) + 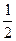О_2(г) = Н₂О_(ж) + 285,83 .

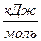Решение. Запишем уравнение реакции образования одного моля метана:

С_{(графит)} + 2H_2(г) = CH_4(г).

Тепловой эффект реакции равен

DH⁰ = ånDH⁰_{сгор. (исх.)} – ånDH⁰_{сгор. (прод.)}.

DH⁰ = – 393,51 + 2∙(–285,83) – (–890,31) = –74,86 .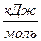

Пример 1.3. Выведите функциональную зависимость изменения молярной изобарной теплоемкости от температуры DC⁰_Р = f(T) для реакции С_{(графит)} + CO_2(г) = 2CO_(г). Вычислите тепловой эффект реакции при 500 К, если при стандартных условиях он равен 172,5 кДж.

Решение. Зависимость C⁰_Р реагирующих веществ от температуры представлена для неорганических веществ уравнениями вида

C⁰_Р = a + bT + c¹T ^–2,

поэтому величину DC⁰_Р рассчитывают по уравнению

D C⁰_Р = Da + DbT +Dc¹T ^–2 .

Выпишем температурные коэффициенты в уравнениях теплоемкости для веществ, участвующих в реакции (см. прил. 1).

Вещество	Коэффициенты уравнения С0P = f (T),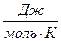
а	b×103	с1×10–5
С(графит)	16,86	4,77	–8,54
СО (г)	28,41	4,10	–0,46
СО2 (г)	44,14	9,04	–8,53

Вычислим их изменения:

Da = 2^. 28,41 – 44,14 – 16,86 = -4,18;

Db = (2^. 4,10 – 9,04 – 4,77)^.10^–3 = -5,61^.10^–3;

Dc¹ = [2^. (–0,46) – (-8,53) – (-8,54)] ^.10⁵ = 16,15^.10⁵.

Функциональная зависимость изменения молярной изобарной теплоемкости от температуры для данной реакции имеет вид:

DC⁰_Р = -4,18 -5,61^.10^–3T + 16,15^.10⁵T ^–2 .

Для расчета теплового эффекта реакции воспользуемся уравнением Кирхгофа в интегральной форме:

.

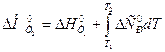После подстановки зависимости D C⁰_p от T в уравнение Кирхгофа и интегрирования получим:

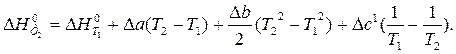
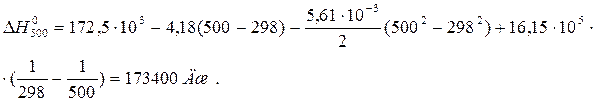
Пример 1.4. Изменение энтропии реакции С_{(графит)} + CO_2(г) = 2CO_(г) при стандартных условиях ( 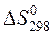) равно 175,46 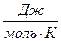). Используя функциональную зависимость теплоемкостей реагирующих веществ от температуры (см. пример 1.3), вычислите изменение энтропии при температуре 500 К ( ).

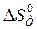Решение. Изменение энтропии реакции при заданной температуре находим по уравнению

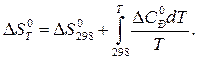
После подстановки DC⁰_Р = Da + DbT +Dc¹T ^–2 и интегрирования получим:

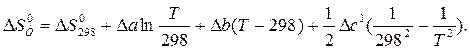
Значения Da, Db и Dc¹ рассчитаны в примере 1.3. Отсюда:

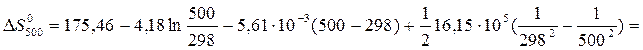= 178,03 .

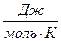Пример 1.5.Константа равновесия K_P газовой реакции А + Б = В равна 0,128·10⁵ Па^–1. Определите состав равновесной смеси (в мол. %), полученной при давлении Р = 10,13·10⁵ Па из 2 моль вещества А и 1 моль вещества Б.

Решение. Обозначим через x равновесное количество вещества В. Так как на образование его должно израсходоваться согласно химическому уравнению реакции по x молей А и Б, то в равновесной смеси останется (2 – x) моль А и (1 – x) моль Б. Запишем количество вещества

число молей:	А + Б = В
в исходной смеси
в равновесной смеси	(2 – x)	(1 – x)	x

∑ n_i = 2 – x + 1 – x + x = 3 – x.

Парциальные давления компонентов P_i рассчитываем по уравнению:

P_i = X_i·P,

где X_i – мольная доля i-го компонента газовой смеси, X_i = ;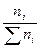

P – общее давление в системе.

Выражения для парциальных давлений компонентов имеют вид:

P_A = 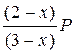; P_Б = 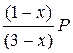; P_В = .

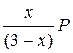Подставим эти выражения в уравнение для константы равновесия реакции:

K_P = 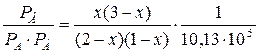= 0,128·10⁵ Па^–1.

После небольших преобразований получим:

2,32 x² – 6,96 x + 2,64 = 0.

Решая квадратное уравнение, находим x₁ = 0,44 и x₂ = 2,55.

Второй корень не имеет физического смысла, т.к. x может быть только меньше 1. Остается значение x = 0,44. Следовательно, в равновесной смеси содержится 2 – 0,44 = 1,56 моль А; 1 – 0,44 = 0,56 моль Б и 0,44 моль В. Состав смеси в мольных процентах определяется из соотношения

X_i = 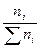·100%,

где ∑ n_i = 1,56 + 0,56 + 0,44 = 2,56.

Определим состав равновесной смеси:

X_A = ;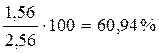

X_Б = ;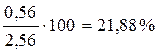

X_В = 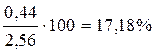.