Теория предельного состояния. Энергетическое условие пластичности. Уравнение пластичности и его анализ
При испытании образца на разрывной машине, т.е. в случае линейного напряженного состояния пластическая деформация наступит тогда, когда главное нормальное напряжение достигнет предела текучести G1 ≥ GT. При каких значениях главных нормальных напряжений наступит пластическая деформация при объемных схемах напряженного состояния?
Ответ на этот вопрос дают теории предельного состояния. Известного 4 теории напряженного состояния.
1. Теория наибольших нормальных напряжений.
Пластическая деформаций наступит тогда, когда наибольшее нормальное напряжение достигнет предела текучести.
Эта теория не учитывает значения G2 и G3 и опытными данными не подтверждается.
2. Теория наибольших деформаций.
Пластическая деформация наступит тогда, когда наибольшая деформация (вытяжка металла) достигнет определенной величины.
Эта теория устарела и не отвечает действительности.
3. Теория разности главных нормальных напряжений.
Пластическая деформация наступит тогда, когда разность двух главных нормальных напряжений (наибольшего и наименьшего) достигнет предела текучести при его данном состоянии.
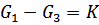
K – предел текучести металла в данном состоянии.
В отличии от GT , определяемого в лабораториях при испытании образцов на растяжение, K – учитывает скорость деформации, температуру и другие факторы, имеющие место в момент деформации металла.
4. Энергетическая теория предельного состояния.
Пластическая деформация в теле наступи тогда, когда потенциальная энергия упругой деформации, направленной на изменение формы тела, а не его объема, достигнет определенного значения.
Энергетическое уравнение пластичности.
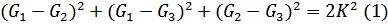
Анализ уравнения пластичности сводится к тому, чтобы установить насколько отличается четвертая от третьей теории предельного состояния.
Три частных случая:
G2 = G1 – G2 – имеет максимальное значение.
G2 = G3 – G2 – имеет минимальное значение.
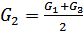 – имеет среднее значение.
– имеет среднее значение.
Если G2 = G1 , то после подстановки этого значения в уравнение (1) получим 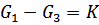
Следовательно четвертая теория совпадает с третьей.
Если G2 = G3, то после подстановки в уравнение (1) получим
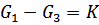
Следовательно при G2 минимальном значении четвертая теория совпадает с третьей.
Если 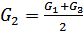 , то после подстановки в уравнение (1) получим
, то после подстановки в уравнение (1) получим
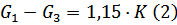
Таким образом при среднем значении G2 четвертая теория отличается от третьей на большую величину.
Уравнение (2) есть уравнение пластичности. В общем виде уравнение пластичности принимает вид:
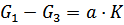
где a = 1,0 ÷ 1,15 – коэффициент, учитывающий влияние среднего главного напряжения G2.
При пользовании уравнением пластичности необходимо учитывать знак главных нормальных напряжений. Напряжения растяжения знак (+), а напряжения сжатия знак (-).
Если за сопротивление деформации принимать максимальное главное напряжение, то исходя из уравнения пластичности, получим:
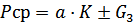
Чем больше разница между G1 и G3 , тем процесс деформации протекает легче, тем меньше и удельное сопротивление.
