Теория активных ансамблей

Теории катализа

Эта теория была создана (1939 г., Кобозев) для катализаторов, представляющих собой нанесенное на инертный носитель активное вещество –собственно катализатор, который находится в микрогетерогенном состоянии в виде коллоидных частиц на поверхности кристалла. Обмен атомами катализатора между отдельными частицами затруднен, т.к. последние зафиксированы на носителе.

Теория основана на двух предположениях:

1. Активный центр катализатора представляет собой ассоциат Ме_n (n= 1,2,3…), называемый активным ансамблем (АА).

2. Поверхность инертного носителя состоит из областей, которые отделены друг от друга геометрическими или энергетическими барьерами (области миграции). Атомы катализатора свободно мигрируют внутри каждой из этих областей, образуя ансамбли с различными n, но не могут перейти в другую область.

Активный ансамбль состоит из определенного числа атомов металла (n_a) внутри области миграции, хотя ансамбли могут содержать разное количество атомов.

Эта теория позволяет на основе экспериментальной зависимости активности катализатора от степени покрытия носителя рассчитать число атомов в активном ансамбле, число областей миграции и активность одного отдельного активного ансамбля. Поскольку активность катализатора максимальна при количестве атомов Ме в ансамблеn_a , то n_a можно определить из зависимости активности катализатора от числа атомов (ν) Ме в одной области миграции.

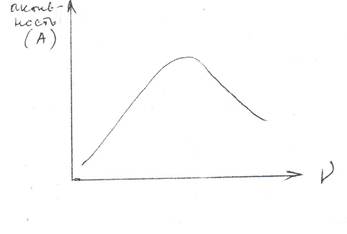
Активность адсорбционного катализатора (это количество вещества, которое прореагировало на 1 г адсорбированного катализатора) равна:

А = Z_n r _n , где

Z_n – число активных ансамблей на поверхности 1 г катализатора,

r _n - активность одного ансамбля.

Число активных ансамблей Z_n можно определить следующим образом:

Z_n = Z_о W_n , где

W_n - вероятность образования активного ансамбля,

Z_о – число областей миграции на поверхности 1 г катализатора.

Z_о = S/Δ, где

S-поверхность 1 г носителя, Δ– средняя поверхность области миграции.

Вероятность образования разных ансамблей зависит от степени покрытия катализатором поверхности носителя, т.е. при любой степени покрытия есть вероятность возникновения любого ансамбля, но наиболее вероятно возникновение какого-то одного.

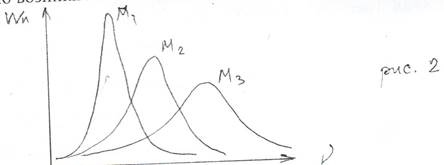
Эта вероятность описывается законом Пуассона:

W_n = (ν^na/ n_a!)e^-ν , где

ν – среднее число атомов катализатора в одной области миграции

ν = N/ Z_о ( N – число атомов Ме, нанесенных на 1 г носителя), также ν = Р ·Θ, где

Р – наибольшее число атомов Ме в области миграции, имеющей среднюю поверхность Δ: Р= Δ/σ_м (σ_м – поверхность 1 атома Ме),