Электрические свойства проводниковых материалов

Электрическим свойством проводниковых материалов является электропроводность – способность материала проводить электрический ток. К основным электрическим параметрам относят: удельное электрическое сопротивление, удельную электрическую проводимость, температурный коэффициент удельного сопротивления и коэффициент теплопроводности.

Удельное электрическое сопротивление для образцов правильной формы:

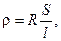(2.1)

где R – сопротивление образца, Ом; S – площадь поперечного сечения образ­ца, м²; l – длина образца, м.

С точки зрения электронной теории твердого тела:

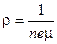, (2.2)

где n – концентрация электронов, м^-3; e – заряд электрона, Кл; μ – подвижность электронов, м²/В·с.

Величину ρ измеряют в Ом·м, однако для прак­тических целей 1 Ом∙м слишком большое значение, поэтому этот параметр чаще всего выражают в более мелких единицах, напри­мер в микроомах на метр. Диапазон значений ρ металлических про­водников (при нормальной температуре) от 0,016 для серебра до 10 мкОм·м для некоторых сплавов.

Значения ρ металлов в нормальных условиях отличаются друг от друга примерно в 100 раз.

Сопротивление проводников R_s на высоких частотах существен­но больше их сопротивления на постоянном токе вследствие того, что высокочастотное поле проникает в проводник на небольшую глубину. Чем выше частота поля, тем на меньшую глубину оно проникает в проводник. Это явление получило название поверхност­ного эффекта. За глубину проникновения тока в проводник на дан­ной частоте условно принимают глубину, на которой плотность тока уменьшается в 2,7 раза по сравнению с ее значением на повер­хности проводника.

Величину, обратную удельному электрическому сопротивлению ρ, называют удельной электрической проводимостью (См/м):

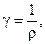(2.3)

Удельное электрическое сопротивление металлов зависит от тем­пературы. Эта зависимость определяется температурным коэффициентом удельного электрического сопротивления (К^-1), который при данной температуре вычисляют по формуле:

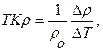(2.4)

где ∆ρ - элементарное приращение сопротивления проводника, соответствую­щее элементарному приращению температуры ∆T.

Кривая изменения удель­ного сопротивления металлического про­водника в зависимости от температу­ры представлена на рисунке 2.1

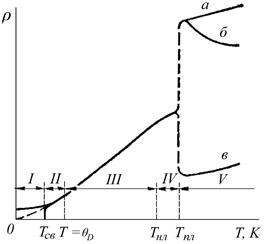
Рисунок 2.1 – Зависимость удельного сопротивления металлического проводника от температуры в широком диапазоне температур:

а, б, в – варианты изменения удельного сопротивления у различных расплавленных металлов.

В узкой области I, составляющей несколько градусов Кельвина, у ряда метал­лов может наступить состояние сверхпроводимости и на рисунке виден скачок удельного сопротивления при температуре T_св. У чистых металлов совершенной структуры при стремлении температуры к 0 К удельное сопротивление также стремится к 0 (пунктирная кривая), а длина свободного пробега устремляется в бесконечность. Даже при обычных температурах длина свободного пробега электронов в металлах в сотни раз превышает расстояние между атомами.

Средняя длина свободного пробега электронов при 0˚С

для ряда металлов ( 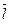10¹⁰, м)

Li 110 Na 350 K 370 Ni 113

Cu 420 Ag 570 Au 410 Fe 220

В пределах переходной области II наблюдается быстрый рост удельного сопротивления ρ ~ Тⁿ, где п может быть до 5 и постепенно убывает с ростом температуры ~ до 1 при Т = θ_D (θ_D – температура Дебая определяет максимальную частоту тепловых колебаний).

Линейный участок (область III) в температурной зависимости ρ(Т) у большинства металлов простирается до температур, близких к точке плавления. Исключение из этого правила составляют ферромаг­нитные металлы, в которых имеет место дополнительное рас­сеяние электронов на нарушениях спинового порядка. Вблизи точки плавления, т.е. области IV, начало которой отмечено на рисунок 1 температурой Т_нл, и в обычных металлах может наблюдаться некоторое отступление от линейной зависимости.

При переходе из твердого состояния в жидкое у большинства ме­таллов наблюдается увеличение удельного сопротивления приблизительно 1,5 – 2 раза, хотя имеют­ся и необычные случаи: у веществ со сложной кристаллической струк­турой, подобных висмуту и галлию, плавление сопровождается умень­шением ρ.

Эксперимент выявляет следую­щую закономерность: если плавление металла сопровождается уве­личением объема, то удельное со­противление скачкообразно воз­растает; у металлов с противопо­ложным изменением объема проис­ходит понижение ρ.

Металлические пленки широко используются в микроэлектронике в качестве межэлементных соединений, контактных площадок, обкладок конденсаторов, магнитных и резистивных элементов интегральных схем. Электрические свойства тонких пленок металлов и сплавов могут значительно отличаться от свойств объемных образцов исходных проводниковых материалов.

На рисунке 2.2 приведены типичные зависимости удельного сопротивления ρ_δ и температурного коэффициента удельного сопротивления α_ρδ от толщины пленки.

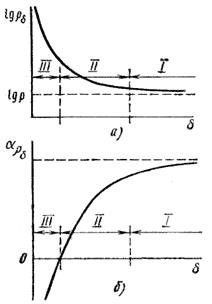
Рисунок 2.2 – Зависимости удельного сопротивления (а)и температурного коэф­фициента удельного сопротивления (б) тонкой металлической пленки от ее толщины.

Пунктиром показаны значения ρ и α_ρ для объемного образца проводника. У большинства пленок в функциональной зависимости ρ(δ) наблю­даются три различные области. Область I соответствует толщине около 0,1 мкм и выше. В этой области удельное сопротив­ление близко к сопротивлению массивного образца. Область II охватывает диапазон изменения δ от 10^-1 до 10^-2 мкм. На этом участке удельное сопротивление пленки уже существенно больше сопротивления массивного образца, а α_ρδ приближается к нулю. Область III, соответствующая толщине порядка 10^-3 мкм, характеризуется очень высоким удельным сопротивлением и отрицательным температурным коэффициентом удельного сопротивления.

Для объяснения показанной зависимости надо принять во внимание, что тонкие пленки на ранних стадиях конденсации имеют островковую структуру, т. е. при малом количестве осажденного металла его час­тицы располагаются на диэлектрической подложке в виде отдельных разрозненных зерен – островков. Электропроводность пленки воз­никает при некотором минимальном количестве осажденного металла, однако еще до образования соединительных мостиков между остров­ками металла. При приложении электрического поля (в плоскости пленки) происходит переход электронов через узкие диэлектрические зазоры между соседними островками. Переход электронов облегчается при повышении температуры. Кроме того, сопротивление пленки островковой структу­ры во многом определяется поверхностным сопротивлением участков подложки, на которых нет зерен металла. А поверхностное сопротив­ление диэлектриков с увеличением температуры падает. Эти причины и обусловливают отрицательный α_ρ пленок малой толщины.

При увеличении количества осажденного металла величина зазо­ров между островками уменьшается, проводимость пленок растет,отрицательный α_ρ становится меньше по модулю, а затем меняет знак. Значение толщины пленки, при которой происходит смена знака α_ρ , зависит от рода металла, условий формирования пленки, концентра­ции примесей, состояния поверхности подложки и в реальных случаях составляет несколько нанометров.

В процессе дальнейшей конденсации вещества на подложке проис­ходит слияние островков и образование сначала проводящих цепочек и каналов, а затем – сплошного однородного слоя. Но и в сплошной пленке удельное сопротивление больше, чем удельное сопротивление исходного проводника, что является следствием высокой концентра­ции дефектов – вакансий, дислокаций, границ зерен, образующихся при срастании островков.

Для сравнительной оценки проводящих свойств тонких пленок поль­зуются параметром сопротивление квадрата R_□(или сопротивление на безразмерный квадрат, или удельное поверхностное сопротивление), численно равным сопротивлению участка пленки, длина которого равна его ширине при прохождении тока через две его противоположные гра­ни параллельно поверхности подложки.

Ввиду того, что R_□ не зависит от величины квадрата, сопротивление тонкопленочного резистора легко рассчитать по формуле:

R = R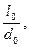_□ (2.5)

где l₀ – длина резистора в направлении прохождения тока; d₀ – ширина пленки.

Для изготовления тонкопленочных резисторов обычно требуются пленки с поверхностным сопротивлением 500 – 1000 Ом/квадрат.