Кинематический расчет привода. Угловая скорость вала электродвигателя
Угловая скорость вала электродвигателя

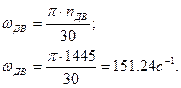
Общее передаточное число привода
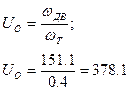
Производим разбивку UO по отдельным ступеням привода
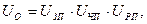
где  передаточные числа отдельных ступеней.
передаточные числа отдельных ступеней.
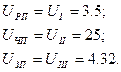
Определяем угловые скорости 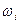 валов привода (рис. 1):
валов привода (рис. 1):
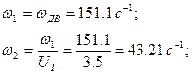
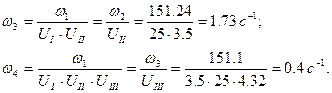
Определяем частоты вращения валов привода:
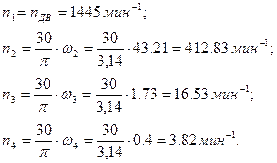
Определяем мощности на валах привода:
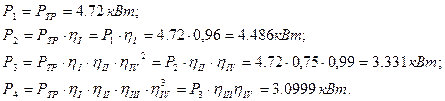
Определяем крутящие моменты на валах привода:
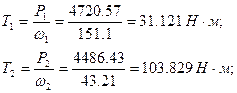

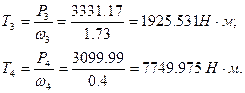
Результаты расчета сводим в табл. 1.
Таблица 1
Сводная таблица результатов кинематического расчета привода.
| № вала | Мощность Р, Вт | Угловая скорость ω, с-1 | Частота вращения п, мин-1 | Крутящий момент Т, Нм |
| Двигатель | 151.24 | 31.12 | ||
| 151.24 | 31.12 | |||
| 43.21 | 412.83 | 103.83 | ||
| 1.73 | 16.53 | 1925.53 | ||
| 0.4 | 3.82 | 7749.98 |
 |
3. Расчет открытых передач
3.1. Расчет ременной передачи 
Основными критериями работоспособности и расчета ременных передач являются: тяговая способность, определяемая величиной передаваемой окружной силы, и долговечность ремня, которая в условиях нормальной эксплуатации ограничивается разрушением ремня от усталости.
Основным расчетом ременных передач является расчет по тяговой способности. Расчет на долговечность ремня выполняется как проверочный.
Промышленностью серийно выпускаются плоские приводные ремни: тканые с полиамидным покрытием и прорезиненные с кордошнуровым несущим слоем. Благодаря прочности, эластичности, низкой чувствительности к влаге и колебаниям температуры, малой стоимости прорезиненные ремни получили большое распространение. Поэтому ниже приводится проектировочный расчет применительно к прорезиненным ремням. Расчет выполняется в следующей последовательности:
1. Определяем диаметры шкивов (рис. 2).
Схема ременной передачи
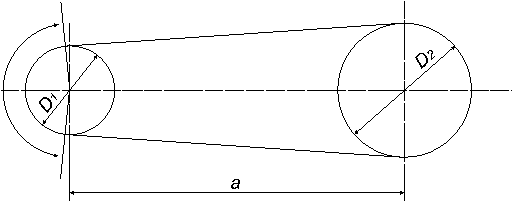
Рис. 2
Диаметр малого шкива
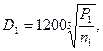
где Р1 – мощность на валу малого шкива, кВт;
п1 – частота вращения малого шкива, мин-1.
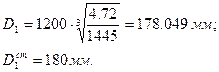
Диаметр большого шкива
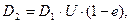
где U – передаточное число; 
е = (0,01–0,02) – коэффициент скольжения ремня.
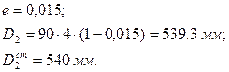
Расчетные диаметры шкивов округлены до стандартных значений по ГОСТ 17282–73 [1].
2. Уточняем передаточное число
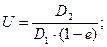
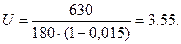
Согласно требованиям расчета значение U не должно отличаться от исходного более чем на 10%.
U = UИСХ
3. Определяем скорость ремня
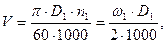
где D1 – диаметр ведущего шкива, мм;
п1 – частота вращения ведущего шкива, мин-1;
ω1 – угловая скорость вращения ведущего шкива, с-1.
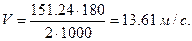
4. Выбираем тип ремня в зависимости от скорости V [1]:
Тип В – спирально-завернутые
5. Определяем межосевое расстояние по формуле
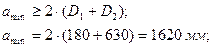
6. Определяем угол обхвата ремнем малого шкива
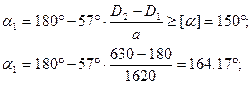

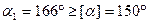
Угол обхвата ремнем малого шкива удовлетворяет необходимым условиям.
7. Определяем длину ремня
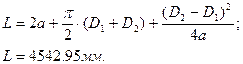
8.Проверяем ремень на долговечность по числу пробегов за 1 с
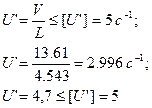
Соотношение 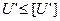 условно выражает долговечность ремня и его соблюдение гарантирует срок службы 1000–5000 ч.
условно выражает долговечность ремня и его соблюдение гарантирует срок службы 1000–5000 ч.
8. Определяют толщину ремня σ.
Для прорезиненных ремней σ рекомендуется определять по условию:
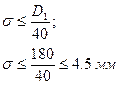
Исходя из стандартной толщины σ1 прокладок, из которых состоит ремень (см. [1]), определяют число прокладок z:
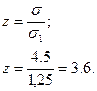
Полученное значение z округляют до меньшего целого числа:
zстанд = 3.
По округленному z определяют фактическую толщину ремня:
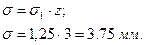
9. Определяем допускаемое полезное напряжение:
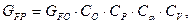
где GFO – номинальное полезное напряжение при стандартных условиях, т.е. для горизонтальной передачи, при угле обхвата α = 180°, скорость V = 10 м/с, спокойной односменной работе. Значение GFO для прорезиненных ремней при напряжении от предварительного натяжения GO =1,8 МПа в зависимости от отношения D1/σ следующее:
 |
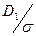 | ||||
| GFO | 2,17 | 2,25 | 2,3 | 2,66 |
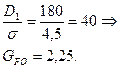
СО – коэффициент, учитывающий расположение передачи. Для горизонтальных и наклонных (до 60°) передач СО = 1, при наклоне от 60° до 80° СО = 0,9, от 80° до 90° СО = 0,8.
СО = 1.
Сα – коэффициент, учитывающий влияние угла обхвата на малом шкиве:
| α° | ||||
| Сα | 0,97 | 0,94 | 0,91 |
α = 166°, найдем коэффициент, соответствующий данному углу методом интерполяции:
10 ––– 0,03
6 –––– x
x = 0,02
Сα = 0,92 + 0,02 = 0,94.
СV – коэффициент, учитывающий влияние напряжения от центробежной силы, уменьшающей сцепление ремня со шкивом:
| V, м/с | |||||
| СV | 1,0 | 0,99 | 0,97 | 0,95 | 0,92 |
V = 27,36 м/с, найдем коэффициент, соответствующий данной скорости методом интерполяции:
5 ––– 0,03
2,36 ––– x
x = 0,014
СV = 0,95 + 0,014 = 0,99.
СР – коэффициент, учитывающ  ий влияние режима работы: при спокойной работе СР = 1, при умеренных колебаниях нагрузки СР = 0,9, при значительных колебаниях нагрузки СР = 0,8, при ударных нагрузках СР = 0,7.
ий влияние режима работы: при спокойной работе СР = 1, при умеренных колебаниях нагрузки СР = 0,9, при значительных колебаниях нагрузки СР = 0,8, при ударных нагрузках СР = 0,7.
СР =1.
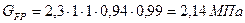
10. Определяем окружное усилие
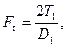
где Т1 – крутящий момент на ведущем валу, Нм;
D1 – диаметр малого шкива, м.
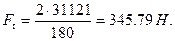
11. Определяем ширину ремня
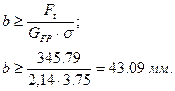
Окончательную ширину ремня принимают по стандарту [1].
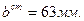
12. Определяем силу предварительного натяжения ремня
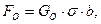
где GO = 1,8 МПа.
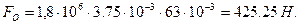
13. Определяем усилие, действующее на вал
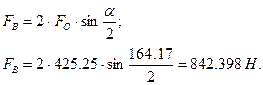
Расчет зубчатой передачи
Расчет цилиндрических прямозубых передач производится в соответствии с ГОСТ 21354–75. Основными видами расчетов являются расчеты на контактную выносливость активных поверхностей зубьев и расчет зубьев на выносливость при изгибе. Так как основной причиной выхода из строя зубьев закрытых передач, работающих при хорошей смазке, является усталостное контактное выкрашивание, то проектный  расчет закрытых передач выполняется на контактную выносливость с последующей проверкой зубьев на контактную выносливость и выносливость при изгибе. Открытые зубчатые передачи рассчитывают на выносливость по напряжениям изгиба.
расчет закрытых передач выполняется на контактную выносливость с последующей проверкой зубьев на контактную выносливость и выносливость при изгибе. Открытые зубчатые передачи рассчитывают на выносливость по напряжениям изгиба.
В данном проекте расчет зубьев на контактную выносливость и выносливость при изгибе ведется при нулевом смещении ( 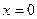 ). В расчетах принят постоянный режим нагрузки, для которого при длительной работе эквивалентное число циклов перемены напряжений
). В расчетах принят постоянный режим нагрузки, для которого при длительной работе эквивалентное число циклов перемены напряжений 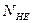 больше базового числа циклов
больше базового числа циклов 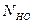 (
( 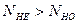 ). Для этого случая коэффициент долговечности
). Для этого случая коэффициент долговечности 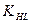 , учитывающий влияние срока службы и режима нагрузки, принимается равным
, учитывающий влияние срока службы и режима нагрузки, принимается равным 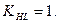
1. Выбираем материал для изготовления зубчатых колес.
Зубчатые колеса в большинстве случаев изготавливают из углеродистой или легированной стали. При выборе марок стали учитывают назначение и тип передачи, требования к габаритам и массе, технологию изготовления, экономическую целесообразность.
Таблица 2
Свойства стали Ст45.
| Марка стали | Механические свойства | Термическая обработка | |||
| Твердость | Предел прочности GB, МПа | Предел текучести GT, МПа | |||
| HB | HRC | ||||
| Ст40Х | 235–262 | – | Улучшение |
2. Ориентировочное значение модуля m вычисляют по формуле:
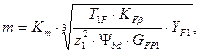
где 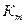 – вспомогательный коэффициент, который для цилиндрических прямозубых передач равен
– вспомогательный коэффициент, который для цилиндрических прямозубых передач равен 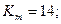
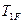 – крутящий момент на валу шестерни, Нм, который принимают из таблицы 1:
– крутящий момент на валу шестерни, Нм, который принимают из таблицы 1:
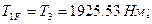
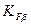 – коэффициент, учитывающий распределение нагрузки по ширине венца, который находится из соответствующего графика в зависимости от значения
– коэффициент, учитывающий распределение нагрузки по ширине венца, который находится из соответствующего графика в зависимости от значения 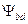 [2].
[2].
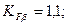
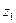 – число зубьев шестерни
– число зубьев шестерни

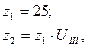
где z2 – число зубьев колеса;
UIII – передаточное число зубчатой передачи.
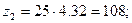
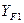 – коэффициент, учитывающий форму зуба, который определяется по графику в зависимости от эквивалентного числа зубьев ZV [2]:
– коэффициент, учитывающий форму зуба, который определяется по графику в зависимости от эквивалентного числа зубьев ZV [2]:
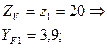
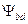 – коэффициент ширины зубчатого венца [1]
– коэффициент ширины зубчатого венца [1]
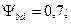
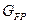 – допускаемые напряжения изгиба зубьев, МПа, который определяется по формуле:
– допускаемые напряжения изгиба зубьев, МПа, который определяется по формуле:
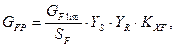
где 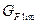 – предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений, МПа, который вычисляется согласно формуле
– предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений, МПа, который вычисляется согласно формуле
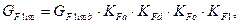
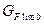 – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа, который определяют в зависимости от способа химико-термической обработки [1].
– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа, который определяют в зависимости от способа химико-термической обработки [1].
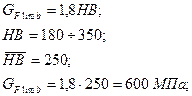
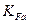 – коэффициент, учитывающий влияние шлифования переходной поверхности зуба. Для зубьев с нешлифованной переходной поверхностью зуба
– коэффициент, учитывающий влияние шлифования переходной поверхности зуба. Для зубьев с нешлифованной переходной поверхностью зуба 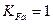 , а для прочих случаев определяют в зависимости от термической или химико-термической обработки: при закалке
, а для прочих случаев определяют в зависимости от термической или химико-термической обработки: при закалке 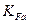 = 0,9; нормализации, улучшении
= 0,9; нормализации, улучшении 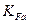 = 1,1; цементации и нитроцементации
= 1,1; цементации и нитроцементации 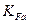 = 0,7.
= 0,7.
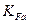 = 1,1;
= 1,1;
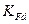 – коэффициент, учитывающий вл
– коэффициент, учитывающий вл  ияние деформационного упрочнения или электрохимической обработки переходной поверхности. Для зубьев колес без деформационного упрочнения или электрохимической обработки переходной поверхности зубьев принимают
ияние деформационного упрочнения или электрохимической обработки переходной поверхности. Для зубьев колес без деформационного упрочнения или электрохимической обработки переходной поверхности зубьев принимают
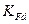 = 1;
= 1;
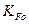 – коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При одностороннем приложении нагрузки
– коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При одностороннем приложении нагрузки
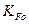 = 1;
= 1;
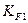 – коэффициент долговечности. Для длительно работающих передач принимается
– коэффициент долговечности. Для длительно работающих передач принимается
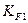 = 1;
= 1;
Учитывая все найденные коэффициенты определим 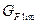 :
:
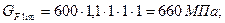
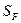 – коэффициент безопасности, который равен
– коэффициент безопасности, который равен
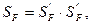
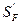 | 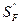 |
| Коэффициент, учитывающий нестаби-льность свойств материала зубчатого колеса и ответственность зубчатой передачи. | Коэффициент, учитывающий способ получения заготовки зубчатого колеса. |
Определяют в зависимости от способа термической и химико-термической обработки и заданной вероятности разрушения. При вероятности разрушения 0,99 и объемной закалке, нормализации и улучшении 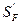 =1,75; при цементации и нитроцементации =1,75; при цементации и нитроцементации 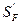 =1,55. =1,55. | Для поковок и штамповок 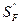 = 1; Для проката = 1; Для проката 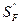 = 1,15; Для литых заготовок = 1,15; Для литых заготовок 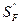 = 1,3. = 1,3. |
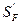 =1,75 =1,75 | 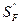 = 1 = 1 |
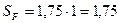
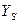 – коэффи
– коэффи  циент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений. При проектном расчете открытых зубчатых передач принимаем
циент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений. При проектном расчете открытых зубчатых передач принимаем
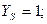
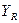 – коэффициент, учитывающий шероховатость переходной поверхности. Для шлифования и зубофрезерования при шероховатости не ниже RZ40 принимают
– коэффициент, учитывающий шероховатость переходной поверхности. Для шлифования и зубофрезерования при шероховатости не ниже RZ40 принимают 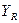 = 1. при полировании
= 1. при полировании 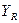 в зависимости от способа термического упрочнения принимают: при цементации, нитроцементации, азотировании
в зависимости от способа термического упрочнения принимают: при цементации, нитроцементации, азотировании 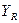 = 1,05; при нормализации и улучшении
= 1,05; при нормализации и улучшении 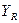 = 1,2.
= 1,2.
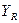 = 1,2;
= 1,2;
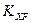 – коэффициент, учитывающий размеры зубчатого колеса. Определяют в зависимости от диаметра вершин зубчатого колеса по специальному графику [1].
– коэффициент, учитывающий размеры зубчатого колеса. Определяют в зависимости от диаметра вершин зубчатого колеса по специальному графику [1].
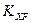 = 1.
= 1.
Определив все величины и коэффициенты, входящие в формулу, находим 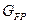 :
:
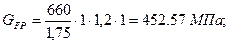
Определяем ориентировочное значение модуля m:
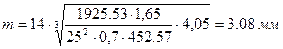
Полученное значение округляем до стандартного в соответствии c ГОСТ 9563–60 [1]:
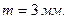
3. Определяем диаметры начальных (внешних) делительных окружностей шестерни и колеса.
Диаметр начальной делительной окружности шестерни:
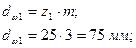
Диаметр начальной делительной окружности колеса:
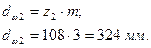
4. Определяе  м межосевое расстояние.
м межосевое расстояние.
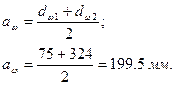
5. Определяем окружную скорость.
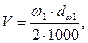
где ω1 – угловая скорость на валу шестерни, с-1,
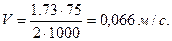
6. Определяем степень точности передачи.
Степень точности выбирают в зависимости от назначения передачи, условий ее работы и возможности производства. Открытые цилиндрические зубчатые передачи обычно выполняют по 9-ой степени точности.
7. Определяем рабочую ширину венца шестерни и колеса.
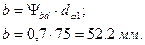
8. Проведем проверочный расчет зубьев на выносливость при изгибе
Расчетное напряжение изгиба зубьев 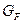 определяют по формуле
определяют по формуле
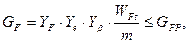
где 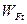 – удельная расчетная окружная сила.
– удельная расчетная окружная сила.
Для цилиндрических прямозубых передач
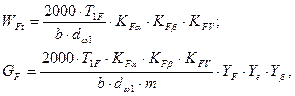
где 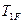 – крутящий момент на валу шестерни, который берется из таблицы 1:
– крутящий момент на валу шестерни, который берется из таблицы 1:
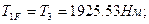
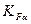 – коэффициент, учитывающий распределение нагрузки между зубьями. Расчет зубчатых колес первоначально производят, предполагая, что в зацеплении находится одна пара зубьев. Тогда
– коэффициент, учитывающий распределение нагрузки между зубьями. Расчет зубчатых колес первоначально производят, предполагая, что в зацеплении находится одна пара зубьев. Тогда
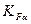 = 1;
= 1;
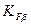 – коэффициент, учитывающий распределение нагрузки по ширине венца. См. п. 2.
– коэффициент, учитывающий распределение нагрузки по ширине венца. См. п. 2.
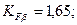
 |
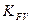 – коэффициент, учитывающий динамическую нагрузку, возникшую в зацеплении:
– коэффициент, учитывающий динамическую нагрузку, возникшую в зацеплении:
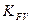 = 1;
= 1;
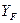 – коэффициент, учитывающий форму зуба. См. п. 2.
– коэффициент, учитывающий форму зуба. См. п. 2.
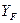 = 4,05;
= 4,05;
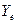 – коэффициент, учитывающий перекрытие зубьев:
– коэффициент, учитывающий перекрытие зубьев:
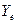 = 1;
= 1;
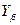 – коэффициент, учитывающий наклон зуба:
– коэффициент, учитывающий наклон зуба:
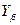 = 1;
= 1;
Определив все величины и коэффициенты, входящие в формулу, находим напряжение изгиба зубьев:
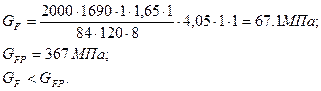
Найденное значение напряжения изгиба зубьев соответствует условиям расчета.
