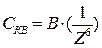Кинетика коагуляции электролитами
В качестве количественной характеристики коагуляции Зигмонди предложил использовать скорость коагуляции.
Скорость коагуляции v – это изменение концентрации коллоидных частиц в единицу времени при постоянном объеме системы.
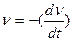 ,
,
где v – концентрация частиц; t – время.
Знак «–» стоит потому, что концентрация частиц со временем уменьшается, а скорость всегда положительна.
Степень коагуляции 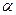 :
:
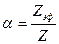
где Z – общее число столкновений частиц в единицу времени; Zэф – число эффективных столкновений (т. е. столкновений, приводящих к коагуляции) в единицу времени.
Если 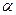 = 0, коагуляция не происходит, коллоидный раствор агрегативно устойчив.
= 0, коагуляция не происходит, коллоидный раствор агрегативно устойчив.
Если 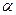 = 1, происходит быстрая коагуляция, т. е. каждое столкновение частиц приводит к их слипанию.
= 1, происходит быстрая коагуляция, т. е. каждое столкновение частиц приводит к их слипанию.
Если 0 < 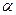 < 1, наблюдается медленная коагуляция, т. е. только некоторые столкновения частиц приводят к их слипанию.
< 1, наблюдается медленная коагуляция, т. е. только некоторые столкновения частиц приводят к их слипанию.
Чтобы частицы при столкновении слиплись, а не разлетелись как упругие шары, должен быть преодолен потенциальный барьер коагуляции 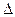 UK. Следовательно, коагуляция произойдет только в том случае, когда коллоидные частицы будут обладать кинетической энергией, достаточной для преодоления этого барьера. Для увеличения степени коагуляции необходимо снижать потенциальный барьер. Это может быть достигнуто добавлением к золю электролита-коагулянта.
UK. Следовательно, коагуляция произойдет только в том случае, когда коллоидные частицы будут обладать кинетической энергией, достаточной для преодоления этого барьера. Для увеличения степени коагуляции необходимо снижать потенциальный барьер. Это может быть достигнуто добавлением к золю электролита-коагулянта.
Зависимость скорости коагуляции от концентрации электролита представлена на рис. 10.1.
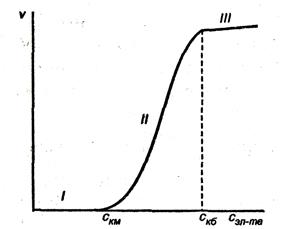
Рис.10.1. Зависимость скорости коагуляции от концентрации электролита
На графике видны три участка:
I. 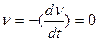 ,
, 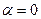 Следовательно, кинетическая энергия kT <<
Следовательно, кинетическая энергия kT << 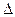 UK, (k – постоянная Больцмана) — лиофобный золь агрегативно устойчив.
UK, (k – постоянная Больцмана) — лиофобный золь агрегативно устойчив.
II. 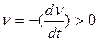 ,
, 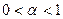 , kT
, kT 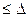 UK т. е. потенциальный барьер коагуляции больше, но соизмерим с кинетической энергией коллоидных частиц, причем с увеличением концентрации электролита-коагулянта он уменьшается, а скорость коагуляции возрастает. Скм – порог медленной коагуляции, Скб – порог быстрой коагуляции. Этот участок кривой выражает зависимость:
UK т. е. потенциальный барьер коагуляции больше, но соизмерим с кинетической энергией коллоидных частиц, причем с увеличением концентрации электролита-коагулянта он уменьшается, а скорость коагуляции возрастает. Скм – порог медленной коагуляции, Скб – порог быстрой коагуляции. Этот участок кривой выражает зависимость:
v = f(с); 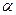 = f{c) ;
= f{c) ; 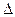 UK = f(c). На этом участке происходит медленная коагуляция.
UK = f(c). На этом участке происходит медленная коагуляция.
III. 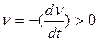 , v
, v 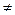 f(с),
f(с), 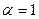 , kT
, kT 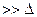 UK т. е. Каждое столкновение приводит к слипанию частиц — идет быстрая коагуляция.
UK т. е. Каждое столкновение приводит к слипанию частиц — идет быстрая коагуляция.
БЫСТРАЯ КОАГУЛЯЦИЯ
Теория быстрой коагуляции, разработанная М. Смолу–ховским в 1916 г., основана на следующих положениях.
1. Рассматриваемая система является монодисперсной, радиус частиц r.
2. 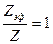 , т. е. все. столкновения являются эффективными.
, т. е. все. столкновения являются эффективными.
3. Рассматриваются только столкновения первичных частиц.
4. Кинетика коагуляции подобна кинетике бимолекулярной реакции:
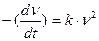
где k – константа скорости коагуляции.
Проинтегрируем это уравнение, разделив переменные:
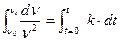
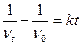 ;
; 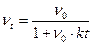 (10.9)
(10.9)
где vo – концентрация частиц золя в начальный момент времени; vt – концентрация частиц золя в момент времени.
Для характеристики быстрой коагуляции используется период коагуляции (период половинной коагуляции) 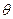 .
.
Период коагуляции ( 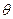 ) – это время, через которое концентрация коллоидных частиц уменьшается в два раза.
) – это время, через которое концентрация коллоидных частиц уменьшается в два раза.
При 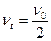 ,
, 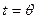
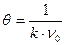 , (10.10)
, (10.10)
Согласно теории быстрой коагуляции, константа коагуляции зависит от коэффициента диффузии и может быть вычислена по уравнению
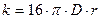 , (10.11)
, (10.11)
Если подставить в это уравнение величину коэффициента диффузии (уравнение 9.5), получим:
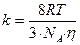 , (10.12)
, (10.12)
Таким образом, зная вязкость дисперсионной среды и температуру, можно вычислить константу скорости быстрой коагуляции. Теория Смолуховского неоднократно проверялась экспериментально и получила блестящее подтверждение, несмотря на сделанные автором допущения.
МЕДЛЕННАЯ КОАГУЛЯЦИЯ
Медленная коагуляция связана с неполной эффективностью столкновений вследствие существования энергетического барьера. Простое введение величины степени коагуляции а в формулы теории Смолуховского не привело к согласию теории с опытом. Более совершенную теорию медленной коагуляции разработал Н. Фукс. Он ввел в кинетическое уравнение коагуляции множитель, учитывающий энергетический барьер коагуляции 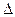 UK:
UK:
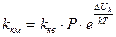 (10.13)
(10.13)
 где kкм – константа скорости медленной коагуляции; kкв – константа скорости быстрой коагуляции; Р — стерический фактор;
где kкм – константа скорости медленной коагуляции; kкв – константа скорости быстрой коагуляции; Р — стерический фактор; 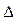 UK – потенциальный барьер коагуляции; k – постоянная Больцмана, равная
UK – потенциальный барьер коагуляции; k – постоянная Больцмана, равная 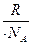 ; NA – постоянная Авогадро.
; NA – постоянная Авогадро.
Таким образом, для расчета константы скорости медленной коагуляции необходимо знать потенциальный барьер коагуляции, величина которого зависит прежде всего от дзета–потенциала.
ФАКТОРЫ УСТОЙЧИВОСТИ
ЛИОФОБНЫХ ЗОЛЕЙ
Фактор устойчивости, или коэффициент замедления W, показывает, во сколько раз константа скорости медленной коагуляции меньше константы скорости быстрой коагуляции.
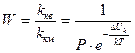 (10.14)
(10.14)
Следует отметить пять факторов устойчивости, среди которых два первых играют главную роль.
1. Электростатический фактор устойчивости.
Он обусловлен наличием ДЭС и дзета–потенциала на поверхности частиц дисперсной фазы.
2. Адсорбционно–сольватный фактор устойчивости.
Он обусловлен снижением поверхностного натяжения в результате взаимодействия дисперсионной среды с частицей дисперсной фазы. Этот фактор играет заметную роль, когда в качестве стабилизаторов используются коллоидные ПАВ, с которыми мы познакомимся позднее.
3. Структурно–механический фактор устойчивости.
Он обусловлен тем, что на поверхности частиц дисперсной фазы образуются пленки, обладающие упругостью и механической прочностью, разрушение которых требует времени и затраты энергии. Этот фактор устойчивости реализуется в тех случаях, когда в качестве стабилизаторов используются высокомолекулярные соединения (ВМС).
4. Энтропийный фактор устойчивости. Коагуляция приводит к уменьшению числа частиц в системе, следовательно, к уменьшению энтропии ( 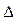 S < 0), а это, как вы помните из термодинамики, приводит к увеличению свободной энергии системы
S < 0), а это, как вы помните из термодинамики, приводит к увеличению свободной энергии системы 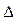 G > 0. Поэтому система самопроизвольно стремится оттолкнуть частицы друг от друга и равномерно (хаотично) распределить по объему системы. Этим обусловлен энтропийный фактор устойчивости. Однако мы помним, что число частиц в коллоидном растворе по сравнению с истинным раствором такой же массовой концентрации гораздо меньше, поэтому роль энтропийного фактора невелика. Но если частицы стабилизированы веществами, обладающими длинными гибкими цепями (ВМС) и потому имеющими много конформаций, то при сближении таких частиц их защитные слои вступают во взаимодействие. Это взаимодействие непременно приводит к уменьшению числа возможных конформаций, а значит – к уменьшению энтропии. Поэтому система стремится оттолкнуть частицы друг от друга.
G > 0. Поэтому система самопроизвольно стремится оттолкнуть частицы друг от друга и равномерно (хаотично) распределить по объему системы. Этим обусловлен энтропийный фактор устойчивости. Однако мы помним, что число частиц в коллоидном растворе по сравнению с истинным раствором такой же массовой концентрации гораздо меньше, поэтому роль энтропийного фактора невелика. Но если частицы стабилизированы веществами, обладающими длинными гибкими цепями (ВМС) и потому имеющими много конформаций, то при сближении таких частиц их защитные слои вступают во взаимодействие. Это взаимодействие непременно приводит к уменьшению числа возможных конформаций, а значит – к уменьшению энтропии. Поэтому система стремится оттолкнуть частицы друг от друга.
5. Гидродинамический фактор устойчивости.
Ему способствует увеличение плотности и динамической вязкости дисперсионной среды.
В реальных системах действуют, как правило, несколько факторов устойчивости. Каждому фактору соответствует специфический способ его нейтрализации. Это затрудняет создание общей теории устойчивости. Пока существуют лишь частные теории.
ТЕОРИЯ УСТОЙЧИВОСТИ ЛИОФОБНЫХ ЗОЛЕЙ –
ТЕОРИЯ ДЛФО (ФИЗИЧЕСКАЯ ТЕОРИЯ)
Современная теория устойчивости, развитая российскими учеными Б. В. Дерягиным и Л. Д. Ландау, получила всеобщее признание. Несколько позднее теоретическая разработка, которая привела практически к тем же результатам, была осуществлена голландскими учеными Фервеем и Овербеком. Поэтому современная теория устойчивости носит имя указанных ученых и известна в литературе как теория ДЛФО (DLVO).
Когда коллоидные частицы подходят очень близко друг к другу, их диффузные слои перекрываются и взаимодействуют. Это взаимодействие совершается в тонкой прослойке дисперсионной среды, разделяющей частицы. Устойчивость лиофобных золей определяется, главным образом, особыми свойствами этих тонких жидких слоев.
Когда две коллоидные частицы, находящиеся в дисперсионной среде, сближаются, вначале они разделены толстым слоем жидкости, который постепенно утончается и в результате становится очень тонким.
После образования тонкого жидкого слоя утончение его может продолжаться, и это еще больше сближает частицы. Утончение жидкого слоя заканчивается либо разрывом его при некоторой малой толщине, либо достижением некоторой равновесной толщины, которая далее не уменьшается. В первом случае частицы слипаются, а во втором – нет. Очевидно, что свойства тонкого жидкого слоя определяют, произойдет ли коагуляция, т. е. определяют устойчивость коллоидов.
Исследования показали, что утончение тонкого слоя при сближении частиц происходит путем вытекания из него жидкости. Когда жидкий слой становится достаточно тонким (толщина его меньше 100–200 нм), свойства жидкости в нем начинают сильно отличаться от свойств жидкости в окружающем объеме. В слое появляется дополнительное давление, которое один из авторов теории ДЛФО Б. В. Дерягин назвал «расклинивающим давлением». По определению Дерягина, оно положительно, когда давление в слое понижено, это противодействует вытеканию из него жидкости, т. е. препятствует сближению коллоидных частиц. Отсюда происходит название «расклинивающее», т. е. давление, которое раздвигает, «расклинивает» частицы. Расклинивающее давление может быть и отрицательным, т. е. повышать давление в слое, ускорять вытекание из него жидкости и способствовать сближению частиц.
Возникновение расклинивающего давления в тонких жидких слоях обусловлено, главным образом, двумя факторами:
1) электростатическое взаимодействие в слое – это силы отталкивания с энергией UОТТ > 0;
2) ван–дер–ваальсовы силы притяжения с энергией Uпр <0.
Результирующая энергия межчастичного взаимодействия U определяется как сумма двух составляющих:
U = Uoтт + (–Uпp) = Uотт – Uпр. (10.15)
Если |UОТТ |> |Uпр|, то преобладают силы отталкивания, коагуляция не происходит, золь является агрегативно устойчивым. В противоположном случае преобладают силы притяжения между частицами, происходит коагуляция.
Рассмотрим количественную интерпретацию этих сил.
ЭЛЕКТРОСТАТИЧЕСКИЕ СИЛЫ ОТТАЛКИВАНИЯ
Электростатическое отталкивание между мицеллами возникает при перекрывании диффузных слоев противоионов. Энергия этого взаимодействия:
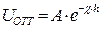 (10.16)
(10.16)
где h – расстояние между частицами; 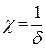 – величина, обратная толщине диффузного слоя
– величина, обратная толщине диффузного слоя 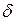 ; А – величина, не зависящая от h и определяемая параметрами ДЭС.
; А – величина, не зависящая от h и определяемая параметрами ДЭС.
Величины 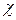 и А могут быть рассчитаны на основе теории ДЭС Расчеты показывают, что энергия отталкивания уменьшается:
и А могут быть рассчитаны на основе теории ДЭС Расчеты показывают, что энергия отталкивания уменьшается:
• при увеличении зарядов противоионов и их концентрации;
• при уменьшении по абсолютной величине 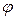 0 и дзета-потенциала.
0 и дзета-потенциала.
Из уравнения (10.16) следует, что 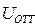 убывает с увеличением расстояния между частицами h по экспоненциальному закону.
убывает с увеличением расстояния между частицами h по экспоненциальному закону.
ВАН-ДЕР-ВААЛЬСОВЫ СИЛЫ ПРИТЯЖЕНИЯ
Энергия притяжения связана, главным образом, с дисперсионным взаимодействием между молекулами. Она может быть рассчитана по уравнению:
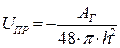 (10.17)
(10.17)
где АГ – константа Гамакера, равная 10–12 эрг. Она рассчитана квантово–статистически и слагается из отдельных констант, характеризующих когезионные[9] и адгезионные[10] взаимодействия.
Из уравнения (10.17) следует, что энергия притяжения изменяется с увеличением расстояния между частицами h обратно пропорционально квадрату расстояния. Таким образом, притяжение сравнительно медленно уменьшается с увеличением расстояния. Так, при увеличении h в 100 раз энергия притяжения уменьшается в 104 раз. В то же время энергия отталкивания уменьшается в 1043 раз.
Результирующая энергия взаимодействия между частицами, находящимися на расстоянии h, определяется уравнением:
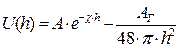 (10.18)
(10.18)
Так как характер зависимости от h для энергии притяжения и отталкивания различный, естественно, что зависимость суммарной потенциальной энергии межчастичного взаимодействия от расстояния между частицами имеет сложный характер. Общий вид этой зависимости U = f(h) представлен на рис. 10.2.
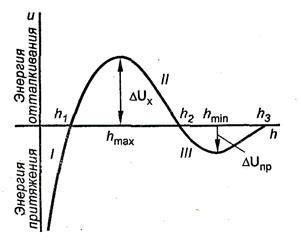
Рис. 10.2 Потенциальная кривая взаимодействия двух коллоидных частиц
На графике есть три участка:
1) 0 < h < h1. U(h)<0, между частицами преобладают силы притяжения, наблюдается ближний минимум.  Происходит коагуляция.
Происходит коагуляция.
2) h1 < h < h2. U(h)<0, между частицами преобладают силы отталкивания.  .
.
h1 < h < h2. U(h)=0 – обнаруживается дальний минимум, однако глубина его невелика.
При h = h1, h2 и h3 U(h) = 0, т. е. при этих расстояниях между частицами силы притяжения уравновешиваются силами отталкивания.
Таким образом, если частицы сблизятся на расстояние меньше h1, они неизбежно слипнутся, но для этого должен быть преодолен потенциальный барьер 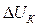 . Это возможно при достаточной кинетической энергии частиц, которая среднестатистически близка к произведению kT.
. Это возможно при достаточной кинетической энергии частиц, которая среднестатистически близка к произведению kT.
Рассмотрим взаимодействие двух частиц. Будем одну частицу считать неподвижной, а вторую – приближающейся к ней с энергией, равной kT.
Если kT < 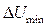 , частицы останутся на расстоянии hmin и будут связаны между собой через слой дисперсионной среды, т. е. образуют «пару», но непосредственно не слипаются и не теряют своей седиментационной устойчивости. В таких случаях говорят, что взаимодействие происходит в дальнем минимуме.
, частицы останутся на расстоянии hmin и будут связаны между собой через слой дисперсионной среды, т. е. образуют «пару», но непосредственно не слипаются и не теряют своей седиментационной устойчивости. В таких случаях говорят, что взаимодействие происходит в дальнем минимуме.
Если 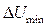 < kT <<
< kT <<  , to частицы при столкновении отлетают друг от друга. Система агрегативно устойчива.
, to частицы при столкновении отлетают друг от друга. Система агрегативно устойчива.
Если kT <  , то происходит медленная коагуляция.
, то происходит медленная коагуляция.
Если kT >  , то происходит быстрая коагуляция.
, то происходит быстрая коагуляция.
Так как золь обычно рассматривают при постоянной температуре, кинетическая энергия частиц остается постоянной. Следовательно, для коагуляции должен быть уменьшен потенциальный барьер коагуляции  .
.
Обычно для понижения потенциального барьера в систему вводится электролит–коагулянт. Теория ДЛФО дает возможность вычислить порог быстрой коагуляции СКВ:
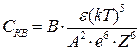 , (10.19)
, (10.19)
где А, В – постоянные величины, которые могут быть рассчитаны; 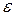 – диэлектрическая проницаемость среды; Z – заряд иона–коагулянта; е – заряд электрона.
– диэлектрическая проницаемость среды; Z – заряд иона–коагулянта; е – заряд электрона.
Из этой формулы видно, что зависимость порога коагуляции от заряда иона-коагулянта, выведенная из теории ДЛФО, согласуется с эмпирическим правилом Шуль–це–Гарди: