Свойства коллоидных растворов

Молекулярно–кинетические свойства обусловлены непрерывным хаотическим движением молекул и атомов. Молекулярно–кинетическая теория изучает законы самопроизвольного движения молекул в жидкостях и газах. Эта теория, разработанная в начале XX в. А. Эйнштейном, имела большое значение, поскольку явилась прямым доказательством существования молекул.

Молекулярно–кинетические свойства коллоидных растворов проявляются в броуновском движении, диффузии и осмосе.

БРОУНОВСКОЕ ДВИЖЕНИЕ

Броуновское движение открыл в 1827 г. английский ботаник Р. Броун. Рассматривая под микроскопом водную суспензию цветочной пыльцы, он обнаружил, что частицы непрерывно двигаются в поле зрения. Некоторые исследователи объясняли обнаруженное Броуном движение жизнедеятельностью пыльцы, однако позднее оказалось, что броуновское движение свойственно всем суспензиям, в том числе и суспензиям неорганических веществ.

Броуновское движение – это непрерывное беспорядочное движение частиц микроскопических и коллоидных размеров, не затухающее во времени. Это движение тем интенсивнее, чем выше температура и чем меньше масса частицы и вязкость дисперсионной среды.

Объяснение этого явления долгое время связывали с внешними причинами – нарушением механического равновесия, температурных условий и т.д. Гуи (1888) и Экснер (1900) предположили, что броуновское движение имеет молекулярно–кинетическую природу, т.е. является следствием теплового движения. Эта точка зрения была подтверждена теоретически Эйнштейном и Смолуховским, а затем экспериментально Перреном, Сведбергом и другими исследователями.

Теперь точно установлено, что броуновское движение обусловлено столкновениями молекул среды, находящимися в непрерывном тепловом движении, с взвешенными в ней частицами микроскопических или коллоидных размеров. В результате этих столкновений частица получает огромное число ударов со всех сторон. Результат этих ударов в значительной степени зависит от размеров частицы.

Если частица имеет сравнительно большие размеры, то число одновременных ударов так велико, что в соответствии с законами статистики результирующий импульс оказывается равным нулю, и частица не будет двигаться под действием молекул среды. Кроме того, частицы с большой массой обладают значительной инерционностью и мало чувствительны к ударам молекул.

Если частица сравнительно мала, то число получаемых ею одновременных ударов со стороны молекул сре­ды значительно меньше, поэтому вероятность неравномерного распределения импульсов, получаемых с разных сторон, увеличивается. Это обусловлено как разным количеством ударов, так и различной энергией молекул среды, сталкивающихся с частицей. В результате частицы приобретают поступательное, вращательное и колебательное движение.

В основе статистической теории, разработанной Эйнштейном и Смолуховским в 1905–1906 гг., лежит следующий постулат.

Броуновское движение совершенно хаотично, т.е. в нем наблюдается полная равноправность всех направлений.

Количественной характеристикой броуновского движения принято считать средний сдвиг частицы 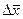за время t, т.е. отрезок прямой, соединяющей начальную точку движения (при t = 0) с положением частицы в момент t в плоскости горизонтальной проекции, наблюдаемой в микроскоп.

Средний квадратичный сдвиг частицы 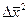при совершенной беспорядочности движения может быть вычислен на основании статистических законов:

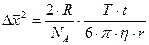(9.1)

где R – универсальная газовая постоянная; N_А – число Авогадро; Т –абсолютная температура; t – время наблюдения; 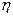– коэффициент вязкости; r – радиус частицы. Следовательно,

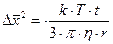(9.2)

где 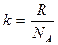– постоянная Больцмана.

Статистическая теория, приводящая к этому уравнению, имеет многочисленные и неоспоримые подтверждения. Результаты, полученные для частиц различной природы и размеров, показали близкое соответствие измеренных и вычисленных величин 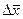, явились блестящим доказательством реальности существования молекул и статистического характера второго начала термодинамики.

Признание молекулярно–кинетической теории послужило толчком к развитию других плодотворных теорий. В коллоидной химии теория броуновского движения оказалась фактически первой количественной теорией.

ДИФФУЗИЯ

Диффузией называется самопроизвольный процесс выравнивания концентрации молекул, ионов или коллоидных частиц под влиянием их теплового движения.

Процесс диффузии является необратимым, он протекает до полного выравнивания концентраций, так как хаотическое распределение частиц отвечает максимальной энтропии системы.

Для количественного описания диффузии используется первый закон Фика:

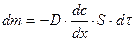, (9.3)

где m – количество продиффундировавшего вещества; D – коэффициент диффузии; 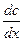– градиент концентрации; S – площадь, через которую происходит диффузия; 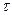– продолжительность диффузии.

Знак минус перед правой частью уравнения (9.3) стоит потому, что производная 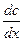отрицательна, так как с увеличением х концентрация уменьшается.

Часто для описания диффузии используется удельный поток диффузии – количество вещества, диффундирующее за единицу времени через сечение единичной площади.

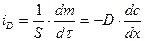(9.4)

Из этого уравнения виден физический смысл коэффициента диффузии D. Коэффициент диффузии численно равен количеству вещества, диффундирующего через единицу площади в единицу времени при градиенте концентрации, равном единице.

А. Эйнштейн (1908) вывел уравнение, связывающее коэффициент диффузии D с абсолютной температурой Т, вязкостью дисперсионной среды 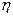и радиусом частиц дисперсной фазы r:

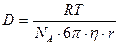(9.5)

Связь между средним квадратичным сдвигом частиц 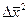и коэффициентом диффузии дает уравнение Эйнштейна—Смолуховского:

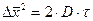(9.6)

Из уравнения (9.6) следует, что сдвиг частиц пропорционален не 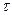, a .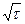

ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ

Осмотическое давление 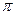достаточно разбавленных коллоидных растворов может быть найдено по уравнению:

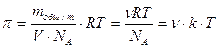, (9.7)

где m_общ – масса растворенного вещества; m — масса одной частицы; V – объем системы; N_A – число Авогадро; Т–абсолютная температура; v – частичная концентрация; k – постоянная Больцмана.

Это уравнение аналогично известному уравнению Вант–Гоффа для осмотического давления истинных растворов:

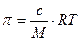
где М – масса одного моля растворенного вещества; с – массовая концентрация.

Молекулярно-кинетические уравнения, справедливые для истинных растворов, применимы и к коллоидным растворам с той лишь разницей, что масса 1 моля вещетва заменяется массой одной частицы. При одной и той же массовой концентрации число частиц (частичная концентрация) в коллоидном растворе значительно меньше, чем в истинном.

Поэтому осмотическое давление лиофобных золей значительно меньше по сравнению с истинными растворами. Весьма малое осмотическое давление лиозолей было причиной ошибки Томаса Грэма, не располагавшего чувствительными осмометрами и считавшего, что у коллоидных растворов осмотическое давление отсутствует.

ЗАКЛЮЧЕНИЕ

Молекулярно–кинетические свойства коллоидных растворов обусловлены хаотическим тепловым движением молекул дисперсионной среды. Средняя кинетическая энергия молекул при постоянной температуре Т постоянна и равна kT, но отдельные молекулы обладают разной кинетической энергией.

Коллоидные частицы постоянно испытывают удары молекул дисперсионной среды, причем количество ударов с разных сторон неодинаково и постоянно меняется. Это и является причиной броуновского движения.

Интенсивность броуновского движения тем больше, чем выше температура, меньше масса частицы и вязкость среды. Результатом броуновского движения коллоидных час­тиц является диффузия – перемещение вещества из области с большей концентрацией в область с меньшей концентрацией, т. е. выравнивание концентрации вещества по всему объему системы. Поскольку равномерное распределение вещества в системе наиболее вероятно, в термодинамическом отношении процесс диффузии идет с увеличением энтропии и поэтому является самопроизвольным. Несмотря на хаотический характер движения всех частиц, перенос вещества происходит вследствие того, что из области с более низкой концентрацией движется больше частиц, чем в обратном направлении. Количество диффундирующего вещества увеличивается с повышением температуры, уменьшением размеров коллоидных частиц и вязкости дисперсионной среды.

Если коллоидный раствор отделен от чистого растворителя (дисперсионной среды) полупроницаемой мембраной, не пропускающей коллоидные частицы, возникает односторонняя диффузия молекул растворителя в коллоидный раствор, называемая осмосом. Причиной осмоса является хаотическое движение частиц. Подобно броуновскому движению и диффузии, осмос является процессом самопроизвольным. Переход растворителя в коллоидный раствор будет происходить до тех пор, пока постоянно возрастающее гидростатическое давление раствора не воспрепятствует ему. Это давление называется осмотическим давлением. Осмотическое давление тем больше, чем больше концентрация коллоидных частиц и чем выше температура.

Рассмотренные молекулярно–кинетические свойства характерны как для истинных, так и для коллоидных растворов, но у последних они выражены значительно слабее, так как при одной и той же массовой концентрации число частиц в коллоидном растворе значительно меньше, чем в истинном.

С молекулярно-кинетическими свойствами мы уже встречались в связи с очисткой коллоидных растворов. Эти свойства имеют также большое значение в связи с проблемами устойчивости коллоидных растворов, к рассмотрению которых мы переходим.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Какие свойства коллоидных растворов относятся к молекулярно–кинетическим?

2. В чем состоит сущность броуновского движения, диффузии, осмоса? Чем они обусловлены?

Являются ли броуновское движение, диффузия и осмос процессами самопроизвольными? Почему?

3. От каких факторов зависит интенсивность каждого из свойств?

4. В чем состоят различия между молекулярно-кинетическими свойствами коллоидных и истинных растворов?

Закончив изучение главы 9, вы должны знать:

• сущность броуновского движения, диффузии, осмоса;

• факторы, от которых зависит каждое из указанных свойств.

ГЛАВА 10

УСТОЙЧИВОСТЬ

КОЛЛОИДНЫХ РАСТВОРОВ.

КОАГУЛЯЦИЯ

Выше (см. главу 6) отмечалось, что образование дисперсных систем сопровождается увеличением свободной энергии системы. Следовательно, дисперсная система является принципиально термодинамически неустойчивой, т.е. рано или поздно должна самопроизвольно разрушиться. Поэтому речь может идти только об относительной термодинамической устойчивости дисперсных систем.

Относительная устойчивость – это способность системы в течение определенного времени сохранять неизменной свою структуру, т.е. размеры, частиц и их равномерное распределение в объеме системы. Относительная устойчивость разных дисперсных систем колеблется в достаточно широких пределах. Как мы увидим дальше, эмульсия без эмульгатора разрушается в течение нескольких секунд с момента ее образования, а красный золь золота, полученный Фарадеем в середине XIX в., «живет» до сих пор.

Следовательно, существуют какие–то причины длительного существования принципиально неустойчивых (термодинамически) систем.

Проблема устойчивости дисперсных систем – одна из важнейших проблем коллоидной химии.

В 1917 году Песков предложил разграничивать относительную устойчивость дисперсных систем как:

а) седиментационную (кинетическую) устойчивость;

б) агрегативную устойчивость.

Эти два вида устойчивости различны по своему механизму и требуют раздельного рассмотрения.