Влияние некоторых факторов на интенсивность теплообмена при пузырьковом кипении

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

Курсовая работа по курсу: «Теория и техника теплофизического эксперимента».

На тему: «Теплообмен при пузырьковом кипении в цилиндре».

Студент группы 02-416:

Любимова Н.А

Руководитель:

Паневин В.И

Москва 2012

Содержание.

1. Теоретическая часть …………………………………………………….…3 1.1.Физические процессы при кипении………………………………......3 1.2.Влияние некоторых факторов на интенсивность теплообмена при пузырьковом кипении……………………………………………………..8

1.3. Теплообмен при кипении. Расчетные формулы……………………15

2. Экспериментальная часть……………………………………………...…18

2.1. Приборы измерения, используемые в установке………………….18

2.2. Оценка погрешности измерения α……………………………….….20

2.3. Теоретическое вычисление α при пузырьковом кипении воды….20

2.4. Эксперимент………………………………………………………….21

2.5. Экспериментальная установка………………………………………22

3. Список используемой литературы………………………………………23

Теоретическая часть.

1.1 Физические процессы при кипении.

Процессы теплообмена при фазовых превращениях (кипении и конденсации) происходят во многих аппаратах криогенных систем и установок; например, в конденсаторах-испарителях ректификационных колонн, ваннах предварительного охлажде­ния, газификаторах и емкостях, системах охлаждения энерге­тических устройств криоатентами и др. Фазовые переходы связаны с изменением структуры вещества и сопровождаются выделением (поглощением) энергии, называемой теплотой фазо­вого перехода.

Теплообмен при кипении зависит от многих факторов: комплекса физических параметров рабочей среды, состояния и формы поверхности, характера образования центров новой фазы, давлении, температуры, теплоты фазового перехода, условий распространения теплоты в каждой из фаз.

Теплообмен при фазовых превращениях, особенно при кипении, отличается большой сложностью и, пожалуй, относится к тем видам теплообмена, для которых имеется наиболее противоречивая и наименее достоверная информация.

Если температура поверхности тела t_w>t_s (где t_s - температура
насыщения жидкости при данном давлении), то на поверхности
будет происходить кипение этой жидкости.

Условием возникновения кипения помимо перегрева жидкости
(t_w >t_s) является наличие центров парообразования (дефекты поверхности, газ, адсорбированный на поверхности, загрязнения).

Плотность теплового потока q и коэффициент теплоотдачи а зависят от величины перегрева Δt_s= t_w - t_s. Это связано с существо­ванием двух основных режимов кипения: образованием на по­верхности отдельных паровых пузырей или сплошной паровой пленки. Первый режим кипения называют пузырьковым, второй - пленочным.

При пузырьковом кипении в большом объеме пограничный слой жидкости разрушается образующимися пузырьками пара, которые всплывают, турбулизируя жидкость и интенсифицируя

теплообмен. При больших плотностях теплового потока (при увеличении At_s) количество образующихся пузырьков возрастает и они образуют на поверхности сплошную паровую пленку. На­ступает пленочный режим кипения.

а) б)

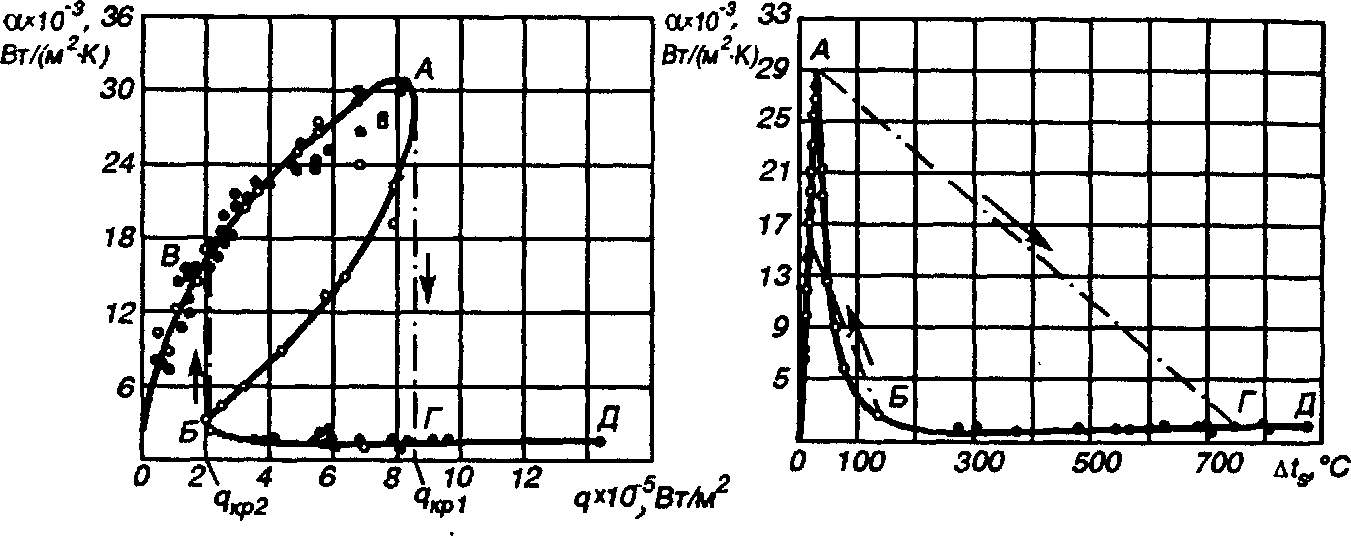
Рис. 1.1.1 Изменение коэффициента теплоотдачи при кипении в большом объеме воды: а - в зависимости от Δt_s , б - в зависимости от q; OA - пузырьковое кипение; БД - пленочное кипение АБ - переходный режим; АГ - мгновенный переход от пузырькового режима кипения к пленочному; БВ - переход от пленочного к пузырьковому режиму кипения; q_кр1 - первая критическая плотность теплового потока; q_кр2 - вторая критическая плотность теплового потока.

Минимальный размер парового пузыря. Пузырьковое кипе­ние происходит путем образования на поверхности нагрева па­ровых пузырей. Пар внутри пузырька испытывает давление жидкости и сжимающее действие сил поверхностного напряжения. Для сферической поверхности раздела фаз превышение
давления в пузыре определяется известным уравнением Лапласа:

Δp=2σ/R (1.1)

где σ - поверхностное натяжение; R - радиус пузыря.

При Δр > 2σ / R паровой пузырь растет, а при Δр < 2σ / R

конденсируется и исчезает.

Связь между изменением давления и температуры насыщения
дается известным уравнением Клапейрона – Клаузиуса:

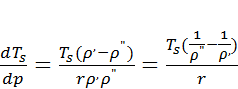(1.2)

Заменяя дифференциалы dT_s и dp конечными приращениями ΔТ_s и Δр, получим

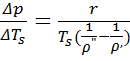(1.3)

индексы (") и (') относятся к пару и жидкости в состоянии насыщения.

Подставляя значение Δр из (1.3) в уравнение Лапласа (1.1), найдем соотношение между минимальным радиусом па­рового пузыря и изменением температуры перегрева Δt_s = t - t_s.

(при этом пренебрегаем величиной l/ρ' по сравнению с l/ρ", так ρ"«ρ')

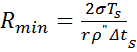(1.4)

Из уравнения (1.4) следует, что чем больше перегрев Δt_s, тем меньше минимальный радиус образующегося пузырька. С увели­чением перегрева количество активных центров парообразования возрастает, так как вступают в действие микровпадины, соответ­ствующие меньшим R_min.

Минимальный размер парового пузыря, определяемый по соот­ношению (1.4), весьма мал. Так, при р=1 бар, t_s=100 С, Δt_s=5K, d_min=l,3 *10^-2мм.

Рост парового пузыря вызывается поступающим в пузырь че­рез границу раздела фаз паром. Изменение радиуса пузыря и ко­личество пара связаны соотношением:

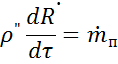
Массовый поток пара 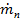вызывает тепловой поток, подво­димый к пузырю через границу раздела фаз,

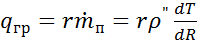(1.5)

Подвод теплоты к пузырю за время τ, находящемуся в боль­шой массе жидкости, имеющей температуру T_s> может быть вы­ражен приближенным соотношением

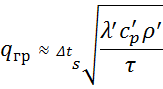
Подставляя значение q_гр в (1.5) и интегрируя, получим

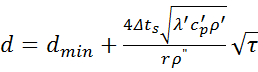(1.6)

Диаметр пузыря d увеличивается за время τ от d_min до значения отрывного диаметра d₀, после чего происходит отрыв пузыря от нагретой поверхности.

Отрывной диаметр. При кипении жидкости в объеме паровые пузыри, достигнув отрывного диаметра d₀, всплывают к свобод­ной поверхности жидкости. Архимедова (подъемная) сила, отры­вающая пузырь от поверхности g(p" - р'), должна преодолеть силу поверхностного натяжения и силу гидродинамического со­противления движению пузыря. Отрывной диаметр do при р=1бар может быть приближенно найден по соотношению

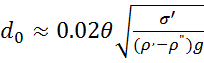(1.7)

где θ - краевой угол или угол смачивания, в град, (для воды θ=50°). При р>1 бар диаметр d_op / d₀ = 1 / р . Из уравнения (1.6) найдем время τ₀ роста пузырька от d_min до отрывного диаметра d₀

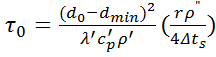_(1.8)

Величина 1/τ₀ есть частота отрывания пузырей. Величина u₀=d₀/τ₀ характеризует скорость роста пузырей на поверхности нагрева. Из (1.7) и (1.8) следует

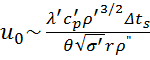_(1.9)

Как видно из уравнения (1.9), скорость роста пузырей увели­чивается с ростом плотности, теплоемкости и теплопроводности жидкости, температуры перегрева и уменьшается с ростом угла смачивания, поверхностного натяжения, плотности пара (давления) и теплоты парообразования. Поэтому в условиях раз­режения наблюдается существенное увеличение роста паровых пузырей и более быстрый переход к пленочному режиму кипения, т.е. ухудшение условий охлаждения. С другой стороны, при от­сутствии центров парообразования перегрев может достигать по­рядка нескольких десятков градусов (например, при кипении на гладкой стеклянной поверхности).

Скорость всплытия пузырей. Известен ряд соотношений для скорости всплытия w" одиночного парового пузыря, в зави­симости от числа Рейнольдса.

Так, при 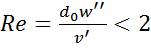по формуле Стокса

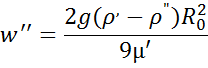
При отсутствии экспериментальных данных скорость всплы­тия может быть определена по приближенной формуле

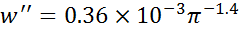_(1.10)

при =0,1...0,4, где π=р/р_кр - приведенное давление.

Время роста и всплытия пузырей составляет от сотых долей до нескольких секунд. Всплытие пузыря занимает значительно больше времени, чем его развитие от d_min до d₀ на поверхности нагрева. Поэтому пузырь пара при подъеме увеличивает свой размер по крайней мере на порядок по сравнению с величиной его отрывного диаметра d₀. Основное количество пара («95% для H₂O) образуется при испарении жидкости в пузыри при их подъ­еме и лишь незначительная часть (≈5% для H₂O) в процессе раз­вития пузырей на поверхности нагрева.

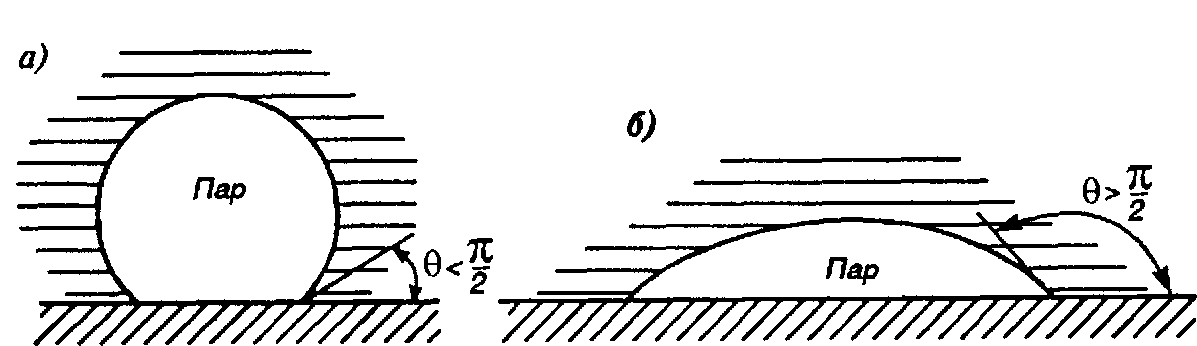
Рис. 1.1.2 Пузырь пара на поверхности нагрева: а - смачивающая поверхность; б - несмачивающая поверхность

Влияние некоторых факторов на интенсивность теплообмена при пузырьковом кипении.

q, Вт/м2

α , Вт/(м2*К)

Влияние давления. Многочисленные данные исследователей свидетельствуют о том, что с ростом давления интенсивность теплообмена в области развитого пузырькового кипения непрерывно увеличивается.

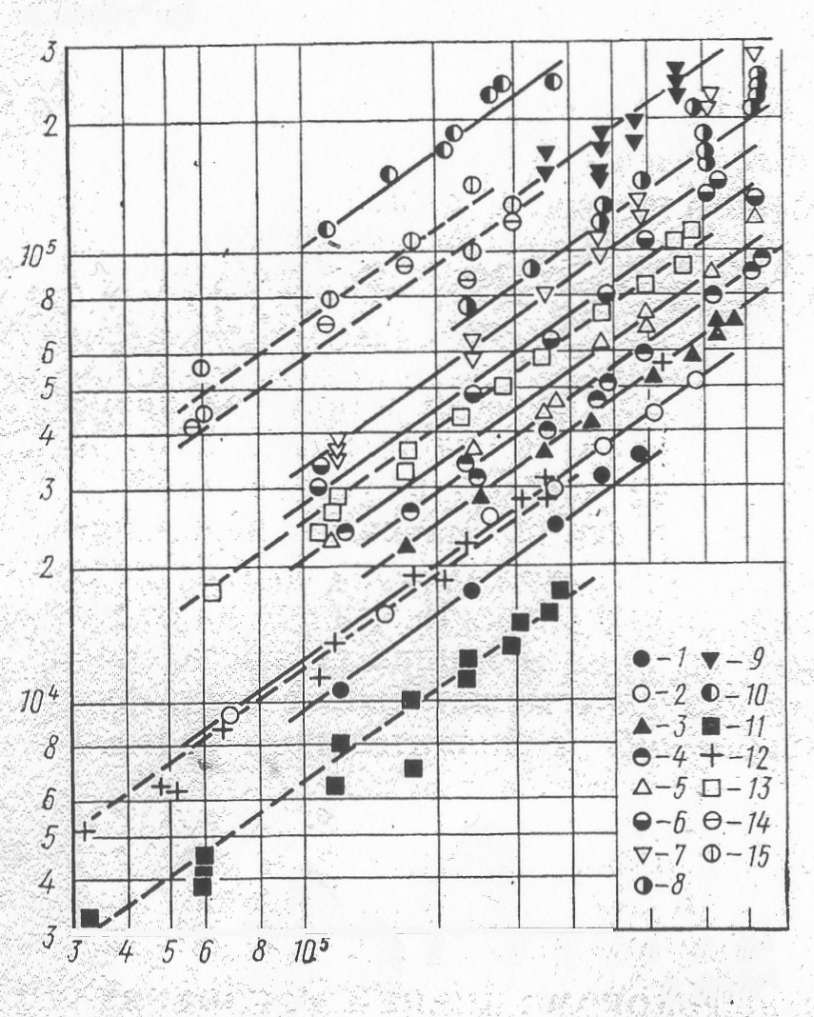
Рис. 1.2.1 Рис. 7.1. Зависимость α от q при кипении воды (______)и этилового спирта (_ _ _) вода (1-10), этиловый спирт (11-15)

Такой ход кривых α=f(p) можно объяснить с молекулярной точки зрения. Действительно, при увеличении давления вследствие повышения температуры насыщения и удельного объема жидкости возрастает кинетическая энергия молекул и, наоборот, ослабевают силы сцепления между ними, т.е работа выхода , а следовательно и энергия поверхностного слоя становится мень­ше. Подтверждением этому служит отрицательный знак производной dσ/dT (для подавляющего большинства жидкостей dσ/dT <0). | Таким образом, с ростом давления облегчаются условия зарождения и роста паровых пузырей: уменьшается критический радиус зародышей паровой фазы и соответственно растет число действующих центров парообразования.

Из рис. 1.2.1 видно, что при всех давлениях во всем исследованном диапазоне изменения плотности теплового потока сохраняется характерная для области развитого пузырькового кипения зависимость α от q . Однако если кипение жидкости осуществляется на полированных поверхностях нагрева при доста­точно низких давлениях (для воды при р < 0,5-10⁵ Па), то кривая кипения заметно деформируется. С понижением давле­ния и повышением класса чистоты обработки поверхность все бо­лее обедняется центрами парообразования и начало кипения сме­щается в сторону более высоких значений плотности теплового потока. Следовательно, на кривой кипения расширяется область конвективного теплообмена в однофазной среде и сокращается интервал изменения q области развитого пузырькового кипения. Переходная зона, в которой действуют оба механизма переноса теплоты, смещается в сторону более высоких значений q.

Явление гистерезиса. При построении зависимо­сти α=f(q) в условиях повы­шения плотности теплового по­тока появление первых паровых пузырей и переход к раз­витому кипению происходят при более высокой плотности теплового потока- q_нк по срав­нению с ее значением, отвеча­ющим прекращению процесса кипения q_пк при проведений опыта в обратном направле­нии. В связи с этим в интервале значений q между q_nк и q_нк ко­эффициенты теплоотдачи в первом случае (опыт с повы­шением q) оказываются меньше, чем во втором. Это объясняется тем, что при переходе от низких к более высоким плотностям теплового потока не все цент­р парообразования соответствующего радиуса кривизны (при данном перегреве жидкости) оказываются активными. Часть из них еще заполнена жидкостью и не может генерировать паровую фазу. При переходе от высоких значений q к более низким практи­чески все центры, соответствующие данному температурному на­пору, являются активными. Рассмотренное явление получило название гистерезиса по тепловому потоку. Коэффициенты теплоотдачи на нижней ветке петли гистерезиса могут быть в два (и более) раза ниже, чем на верхней. Это всегда следует учитывать при обоб­щении опытных данных, полученных в переходной области.

Влияние гравитации. В современной технике возникает необходимость расчета интенсивности теплообмена при кипении в условиях пониженного уровня гравитации или, наобо­рот, при значительных перегрузках.

Применение испарительного охлаждения в быстро вращающих­ся элементах машин, а также перспективы использования пароге­нераторов в космосе привлекли внимание ученых к исследова­ниям процесса теплообмена при кипении как в условиях ослаблен­ного гравитационного поля, так и при перегрузках. Повышенный уровень гравитации (перегрузка) в опытах имитируется полем центробежных сил при размещении экспериментальных установок на центрифугах. В этом случае давление по высоте слоя жидкости от поверхности раздела фаз к обогреваемому днищу вращающего­ся сосуда увеличивается, вследствие чего растет локальное значе­ние температуры насыщения. При достаточно больших перегруз­ках температура жидкости на любом расстоянии от теплоотдающей поверхности по направлению действия центробежной силы может оказаться ниже соответствующей температуры насыщения. В этом случае жидкость по всему объему не кипит и тепловой по­ток отводится от стенки естественной конвекцией, действующей в однофазных средах. Увеличение плотности теплового потока при постоянном уровне перегрузки приводит сначала к закипанию жид­кости в слоях, расположенных у поверхности раздела фаз, а затем кипение распространяется в глубь рабочего сосуда. При некотором значении плотности теплового потока температура жидкости у теплоотдающей поверхности достигает температура насыщения, соответствующей установившемуся здесь давлению. В этом случае кипение наблюдается пo всему объему жидкости. Повышение пе­регрузки при постоянном значении q вытесняет область кипений из глубинных слоев к зеркалу жидкости. Очевидно, что при обработке результатов таких экспериментов возникают существенные трудности, например при выборе определяющей температуры жидкости, по которой следует рассчитывать коэффициент теплоотдачи и вести обобщение опытных данных. Ю. А. Кириченко и его сотрудники пониженный уро­вень гравитации создавали воздействием магнитного поля на исследуемый объем жидкости, помещенный между полюсами магни­та, или разложением силы тяжести на составляющие при проведе­нии опытов в узких щелевых контейнерах, наклоненных под разны­ми углами к горизонту. В опытах Р. Зигеля, а также С. Усыскина с Р. Зигелем контейнер с кипящей жидкостью размещался на па­дающей платформе.

Несмотря на экспериментальные и методические трудности накопленные к на стоящему времени, опытные данные позволяют сделать определенные выводы о влиянии массовых сил на локаль­ные характеристики процесса парообразования и на интенсивность теплообмена при кипении.

Рассмотрим влияние массовых сил на интенсивность теплооб­мена при кипении. С ростом перегрузки усиливается интенсивность переноса теплоты конвекцией, поэтому минимальное значение плотности теплового потока q_мин при котором устанавливается развитое пузырьковое кипение, увеличивается. При q<q_мин влияние механизма переноса, обусловленного процессом парообра­зования, с уменьшением плотности теплового потока ослабе­вает.

В условиях развитого кипения интенсивность теплообмена практически не зависит от перегрузки и при прочих равных условиях определяется плотностью теплового потока. По опытным дан­ным, при q=26 ООО Вт/м² влияние перегрузки на коэффици­ент теплоотдачи кипящему фреону-12 (давление у поверхности раздела фаз р=0,75-0,95 МПа) проявляется только при η>200_. При q= 160 ООО Вт/м² перегрузка начинает влиять на α только при η>800. По опытным данным, заметное увеличение коэффици­ента теплоотдачи при кипении гелия наблюдалось только при перегрузках η> 100.

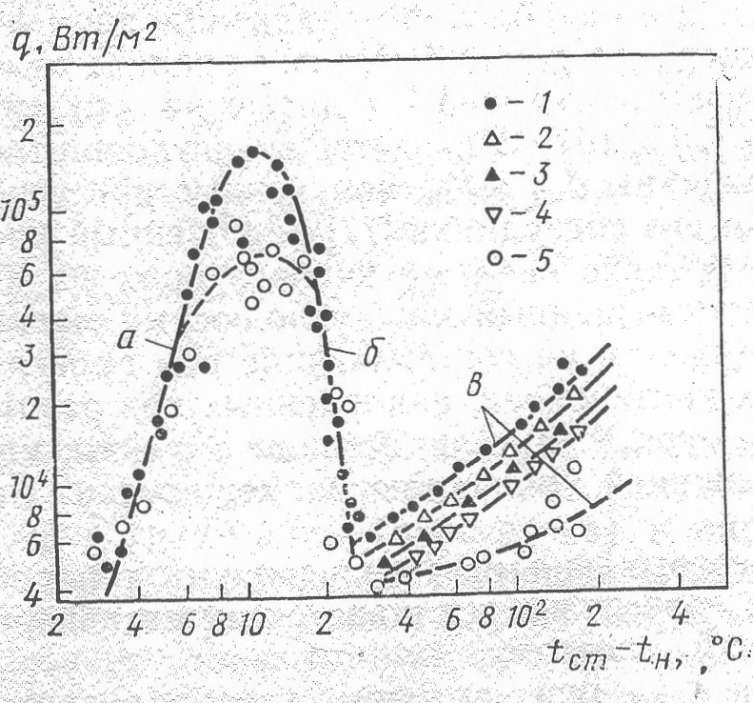
Рис.1.2.2. Зависимость q от Δt при пузырь­ковом кипении азота [η= 1,0 и η= 0 (сво­бодное падение)]. Пленочное кипение азо­та при 0<η <1,0: а -пузырьковое кипение; б — переходная об­ласть; в — пленочное кипение; 1 —η=1.0; 2 - η=0.6; 3 - η=0.33 4- η=0.2; 5 - 0.01<η<0.03

При кипении жидко­стей в условиях ослаблен­ного гравитационного по­ля в интервале значений η от 0,04 до 1,0 интенсив­ность теплообмена также не зависит от уровня гра­витации. Аналогичные результаты получены при кипении азота (рис. 1.2.2) в опытах X. Мерта и Д. Кларка, экспериментальная установка которых поме­щалась на падающей с высоты 10 м платформе. Из рис. 1.2.2 видно, что при развитом кипении (кривая а) и в переходной области от развитого кипе­ния к пленочному (кри­вая б) интенсивность теплообмена не зависит от уровня гравитаций. Мас­совые силы влияют только на значение критической плотности теплового потока q_кр и на интенсив­ность теплообмена при пленочном кипении (кри­вые в). В условиях пол­ной невесомости длитель­ное пузырьковое кипение возможно только в том случае, если каким-либо искусственным способом будет организован отвод паровых пузырей от теплоотдающей поверхности. Итак при пузырьковом кипении в большом объёме снижение уровня гравитационного поля на два порядка по сравнению с земным или повышение перегрузки на два порядка не влияет на ин­тенсивность теплообмена.

Влияние ориентации теплоотдающей поверхности. Коэффициент теплоотдачи при пузырьковом кипении практически не зависит от ориентации теплоотдающей поверхно­сти. Исключение составляют горизонтальные плиты, обращенные теплоотдающей поверхностью вниз. В этом случае эвакуация паро­вых пузырей от поверхности затруднена и поэтому интенсивность теплообмена оказывается ниже, чем от плиты, обращенной теплоотдающей поверхностью вверх.

Если теплоотдающая поверхность выполнена в виде вертикаль­ного пучка труб или одиночной трубы достаточно большой высоты, то в верхней ее части скорость поднимающегося вверх пара может оказаться настолько большой, что повлияет (в сторону повышения) на коэффициент теплоотдачи. То же самое относится к горизонталь­ным пучкам труб: на верхних трубах горизонтального пучка коэф­фициент теплоотдачи может быть выше, чем на нижних. Влияние скорости паровой фазы особенно сильно проявляется при малых плотностях теплового потока, так как в этом случае значительная доля теплоты выносится из пристенной области конвекцией.

Влияние уровня жидкости. При пузырьковом кипении влияние уровня практически не сказывается на интенсивности теп­лообмена до тех пор, пока слой жидкости над теплоотдающей поверхностью не превращается в пленку, толщина которой соизме­рима с отрывным диаметром пузыря. По мере уменьшения толщи­ны пленки δ_пл коэффициент теплоотдачи увеличивается.

Опыты В. Я. Толубинского показали, что при кипении во­ды под атмосферным давлением возрастание коэффициента теплоотдачи с уменьшением уровня наблюдалось только при плотно­стях теплового потока менее 100 кВт/м². При q>100 кВт/м² рост α не наблюдается вплоть до толщин разрыва плёнки термокапиллярными силами. Результаты этих опытов представлены на рис. 1.2.3, а. Здесь по оси ординат отложено отношение коэффициента теплоотдачи при кипении в пленке к коэффициенту теплоотдачи в большом объеме α_б.о, т. е. при достаточно большом уровне жидкости. На рис. 1.2.3, б показано влияние уровня h на α при кипении воды по опытным данным Якоба и Линке.

До настоящего времени нет единой точки зрения на причину возрастания коэффициента теплоотдачи при уменьшении толщины пленки. Отсутствуют также обобщенные зависимости для расчета коэффициента теплоотдачи в тонких пленках в условиях, когда нет принудительного движения жидкости. Реко­мендуют формулы для расчета интенсивности теплообмена при ки­пении криогенных жидкостей в тонких пленках. Однако каждая из трех рекомендованных формул обобщает опытные данные, относя­щиеся только к данной группе жидкостей: 1 — для расчета α при кипении азота, кислорода, аргона; 2 — для расчета α при кипении водорода и неона; 3 — при кипении гелия. Следует отметить, что все рекомендованные в работе формулы сопоставлены с опыт­ными данными, полученными только при давлении 1,0 -10⁵ Па.

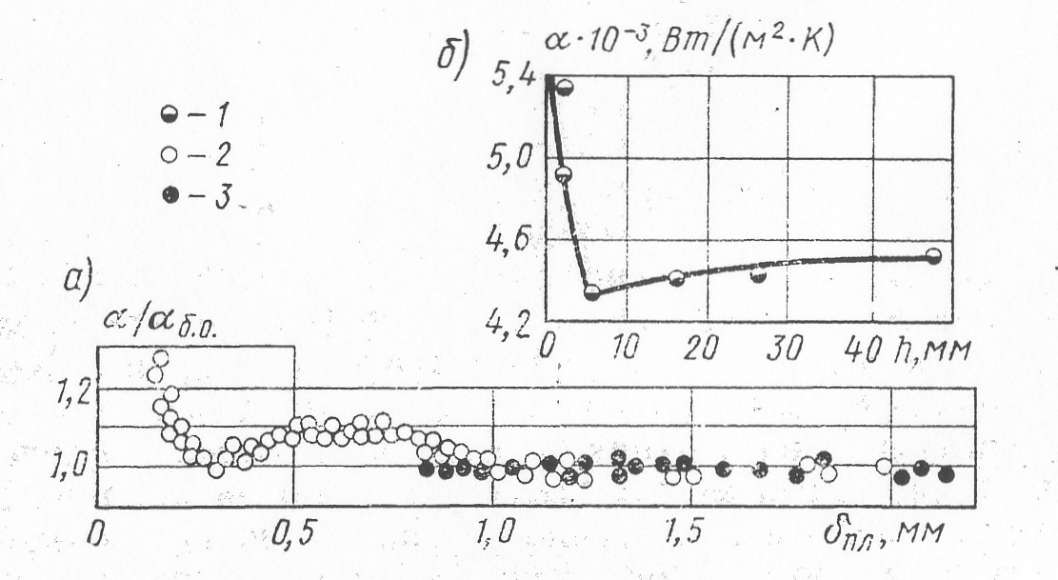
Рис. 1.2.3 Зависимость коэффициента теплоотдачи от толщины пленки δпл (а) и на высоты уровня жидкости h (б) при кипении воды на горизонтальной плоской поверхности (p=1.0*105 Па) 1-q=42кВт/м2; 2-q=26 кВт/м2; 3 – q=610 кВт/м2

Влияние шероховатости теплоотдающей поверхности. В процессе кипения паровые пузыри, возникнове­ний которых способствует интенсификации теплообмена, всегда зарождаются на теплоотдающей поверхности, поэтому состояние последней (чистота, шерховатость), а также ее физико-химические и теплофизические свойства при определенных условиях могут оказывать заметное влияние на интенсивность теплообмена. При прочих равных условиях число действующих центров парообразо­вания зависит от формы и размеров микровпадин, т. е. от микрогео­метрии (шероховатости) теплоотдающей поверхности. С повышением класса чистоты обработки поверхности уменьшаются разме­ры микровпадин, поэтому при прочих равных условиях число активных зародышей паровой фазы и соответственно коэффициент теплоотдачи на гладкой поверхности оказываются меньше, чем на шероховатой.

Влияние физико-химических и теплофизических свойств теплоотдающей поверхности. При за­рождении паровых пузырьков затрачивается энергия на совершение работы против сил адгезии (работа, обусловленная образова­нием на твердой стенке поверхности раздела между фазами, зави­сящая от физико-химических свойств поверхности и свойств кипя­щей жидкости). Поэтому при прочих равных условиях интенсив­ность теплоотдачи к жидкости, кипящей на поверхностях нагрева, выполненных из разных материалов, может быть различной. Од­нако для таких поверхностей, как нержавеющая сталь, латунь, хромированная медь, интенсивность теплообмена оказывается практически одинаковой.