Молекулярная масса и молекулярно-массовое распределение полимеров

Большинство синтетических полимеров состоит из макромолекул различной длины, т.е. являются полидисперсными вследствие статистического (случайного) характера элементарных реакций синтеза и возможности деструкции макромолекул. Биополимеры обычно однородны по молекулярной массе (ММ), однако при выделении полимеров некоторые связи разрушаются и биополимеры становятся полидисперсными.

Вследствие полидисперсности полимеры характеризуют средними ММ и в зависимости от типа усреднения различают среднечисловую и среднемассовую ММ.Существуют и другиетипы усреднения, так при исследовании гидродинамических свойств полимеров определяют среднегидродинамические ММ. Такие ММ определяют при измерении вязкости (средневязкостная – 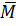_η), константы седиментации (среднеседиментационная – 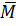_S) или коэффициента диффузии (среднедиффузионная – 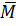_D).

Среднечисловая молекулярная масса определяется соотношением:

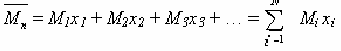
N – число макромолекул,

x_i – числовая доля макромолекул с молекулярной массой M_i.

x_i= N_i / ∑N _i.

Экспериментально 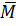_n измеряют методами, в основе которых лежат коллигативные свойства растворов (зависящие от числа частиц). К таким методам относят осмометрию, криоскопию, эбулиоскопию и анализ концевых групп.

Среднемассовая молекулярная масса определяется соотношением:

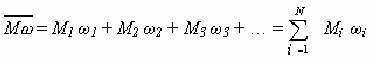
N – число макромолекул,

ω_i – массовая доля макромолекул с молекулярной массой:

M_i. ω_i = N_i M_i / ∑N _i M_i .

Экспериментально M_ω определяют методом светорассеяния. Величина

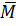_ω > 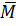_n для полидисперсного образца и 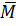_ω = 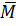_n для монодисперсного образца. Значения 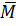_ω более чувствительны к наличию в образце высокомолекулярных фракций, а 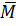_n – к наличию низкомолекулярных фракций.

Отношение 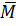_ω / 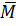_n =К_D называется показателем полидисперсности.

К_D=1 полимер монодисперсен,(редкий случай).

К_D>1 полимеры полидисперсны (для большинства синтетических и природных полимеров),причём К_Dможет изменяться в широких пределах ( от 2 до 20).

Значения показателя полидисперсности К_D связаны с механизмом образования полимера.

К_D=1,5 для продукта радикальной полимеризации при обрыве цепи рекомбинацией;

К_D=2 – при обрыве цепи диспропорционированием.

К_D=1 + Х, где Х – конверсия. Для полимеров, полученных поликонденсацией. При Х→1 (100%) К_D=2.

Для характеристики полидисперсности полимеров, кроме показателя полидисперсности, используются кривые молекулярно-массового распределения (ММР).Различаютинтегральныеидифференциальные функции ММР (рис. 1), которые могут быть числовыми и массовыми. Интегральная кривая ММР – это зависимость между ММ и интегральной массовой (или числовой) долей фракций полимера.

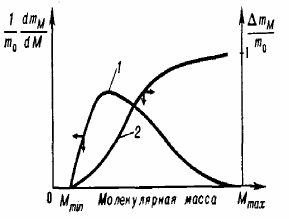
Рис. 1. Кривые интегрального (2) и дифференциального (1) массового ММР полимера.

Здесь ∆ m / m₀ – относительная интегральная доля фракций,

а (1/ m₀)(d m/d M) - – массовая доля фракций.

Дифференциальная кривая ММР представляет собой зависимость ММ от массовой [молекулярно-массовое распределение (ММР) (рис.2, кривая 2)] или числовой доли фракции [молекулярно-числовое распределение (МЧР) (рис. 2, кривая 1)]. Кривые МЧР и МР не совпадают, т.к на числовое распределение большое влияние оказывают низкомолекулярные фракции, а на массовое распределение влияют высокомолекулярные фракции. Абсцисса центра тяжести площади, ограниченной кривой ММР, равна Mω , а абсцисса центра тяжести площади, ограниченной кривой МЧР, равна M_n (рис.2). Кривые распределения могут иметь один (унимодальные), два (бимодальные) или несколько максимумов (полимодальные).

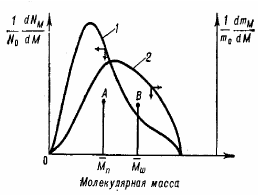
Рис. 2. Дифференциальные кривые МЧР (1) и ММР(2).

При одинаковой средней ММ полимеры могут иметь различное ММР – узкое (на рис. 3, кривая 2) и широкое (рис. 3, кривая 1).

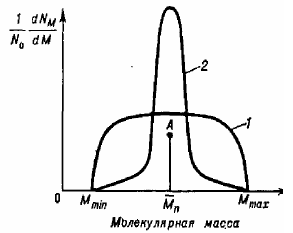
Рис. 3. Кривые ММР с различной полидисперсностью и одинаковым значением средней ММ.