Энергия кристаллической решетки

Энергия кристаллической решетки представляет собой работу, которую нужно затратить для разрушения решетки, т.е. для разведения составляющих ее ионов на бесконечно большое расстояние в вакууме. Энергию кристаллической решетки рассчитывают на моль исследуемого вещества. Для оценки этой энергии воспользуемся модельным методом, который был предложен М. Борном (1920 г.). Рассмотрим два противоположно заряженных иона, составляющих данную кристаллическую решетку, которые имеют абсолютные заряды z₁e₀ и z₂e₀ (e₀— элементарный заряд) и находятся друг от друга на расстоянии r. Силу электростатического взаимодействия (притяжения) между этими ионами можно определить по закону Кулона:

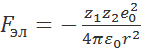, (2.2.1)

где ε₀ — диэлектрическая постоянная вакуума, равная 0,88542•10^–11 Ф/м.

Можно предположить, что первый ион закреплен в положении r = 0, а сила Fэл действует на второй ион в направлении первого иона (рис. 2.1). Поскольку направление силы Fэл противоположно направлению оси r, то Fэл < 0. Одновременно на ионы действует сила отталкивания Fот, обусловленная взаимодействием электронных оболочек и не позволяющая ионам бесконечно близко подойти друг к другу.

Предположим, что сила Fот также приложена ко второму иону. Поскольку направление этой силы совпадает с направлением оси r, то Fот > 0. Силу Fот можно представить в виде

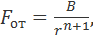(2.2.2)

где В и n - константы, причем n > 1.

Таким образом, суммарная сила взаимодействия ионов равна

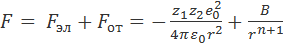. (2.2.3)

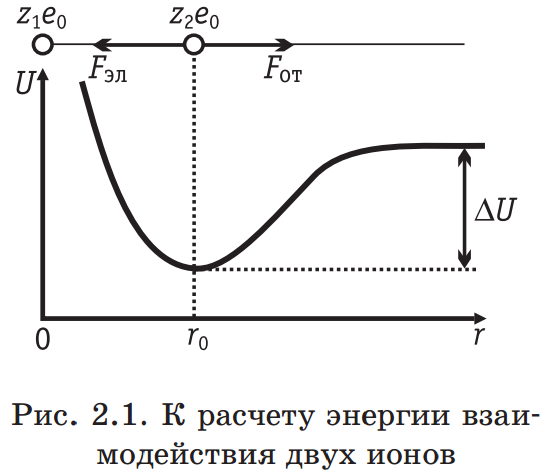
По определению, 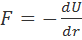, где U—потенциальная энергия системы. Поэтому, интегрируя величину Fот равновесного расстояния (r₀) между ионами в кристаллической решетке до r = ∞, находим изменение потенциальной энергии ∆U, соответствующее удалению двух рассматриваемых ионов на бесконечно большое расстояние (см. рис. 2.1):

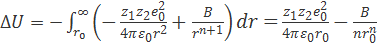. (2.2.4)

Константу В можно рассчитать по уравнению (2.2.3), так как в равновесном состоянии, когда r=r0, F=0. Следовательно,

,

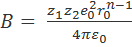а уравнение (2.2.4) можно переписать в виде

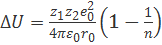. (2.2.5)

Формула (2.2.5) получена для одной пары ионов. Чтобы перейти к энергии кристаллической решетки, рассчитываемой на моль вещества, необходимо умножить ∆U на число Авогадро N_A и учесть взаимодействие между всеми ионами, которое определяется их взаимным расположением в объеме решетки. Последняя поправка эквивалентна введению еще одного множителя А - так называемой константы Маделунга, которая зависит от типа кристаллической решетки. Например, для хлорида натрия

A = 1,7476.

Таким образом, модель Борна, связывающая свободную энергию кристаллической решетки с потенциальной энергией взаимодействия образующих ее ионов, приводит к формуле

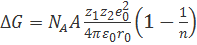. (2.2.6)

Рентгеноструктурный анализ позволяет установить геометрию кристаллов и определить параметры А и r₀. Константа n обычно рассчитывается из данных по сжимаемости кристаллов.

Для NaCl n=7,5; для других солей значение n колеблется от 5 до 12.

Расчет по формуле (2.2.6) показывает, что для хлорида натрия энергия кристаллической решетки составляет

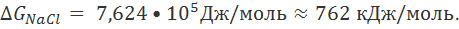
Столь же значительные величины получаются и для других солей.

Для оценки точности формулы (2.2.6) представляет интерес сопоставить 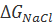с изменением энтальпии в ходе разрушения кристаллической решетки хлорида натрия 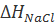. Величину 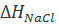можно определить при помощи следующего термодинамического цикла:

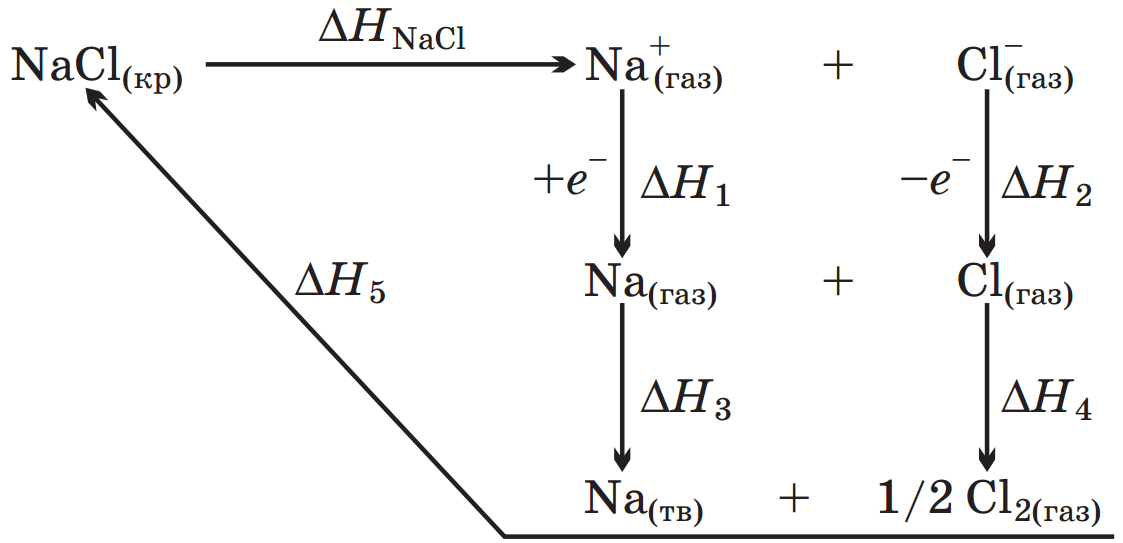
Значение ∆H₁ в первом приближении можно приравнять потенциалу ионизации натрия, взятому с обратным знаком. Изменение энтальпии ∆H₂ приближенно определяется сродством к электрону атома хлора. Величина ∆H₃ соответствует тепловому эффекту при конденсации газообразного натрия, а ∆H₄— тепловому эффекту при рекомбинации атомов хлора. Наконец, ∆H₅ равно тепловому эффекту при сжигании металлического натрия в атмосфере газообразного хлора. Экспериментально было найдено, что ∆H₁ = –496, ∆H₂ = 365, ∆H₃ = –109, ∆H₄ = –121 и ∆H₅ = –411 кДж/моль. Поскольку в замкнутом термодинамическом цикле по закону Гесса Σ∆H_i =0, то

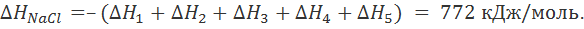
Учитывая данные по теплоемкости хлорида натрия, можно оценить произведение T∆S, которое при 25°С составляет приблизительно 15 кДж/моль. Таким образом, для энергии кристаллической решетки NaCl получаем , что хорошо согласуется с величиной, рассчитанной по формуле (2.2.6).

Итак, образование ионов при разрушении кристаллической решетки требует затраты очень большой энергии. Если бы эта энергия не компенсировалась энергией сольватации, то степень диссоциации практически равнялась бы нулю. Константа диссоциации NaCl в водном растворе при этом составила бы

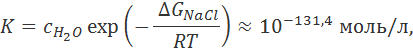
и, следовательно, согласно формуле (1.2.4), степень диссоциации

для 0,01M раствора была бы равна

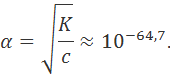
Этот результат показывает, что возражения критиков теории Аррениуса, игнорировавшей ион-дипольное взаимодействие, были вполне обоснованными.

Энергия сольватации

Энергия сольватации представляет собой выигрыш в энергии, который получается при перенесении моля исследуемых ионов из вакуума в данный растворитель. При этом предполагается, что такой выигрыш энергии не включает в себя электростатическое взаимодействие ионов, которое неизбежно сказалось бы уже при введении в растворитель второго и каждого последующего ионов. Чтобы избежать этого осложнения, раствор нужно поддерживать электронейтральным, т.е. вводить в него соответствующее количество ионов противоположного знака, а взаимное притяжение катионов и анионов элиминировать достаточным (теоретически бесконечным) разбавлением раствора.

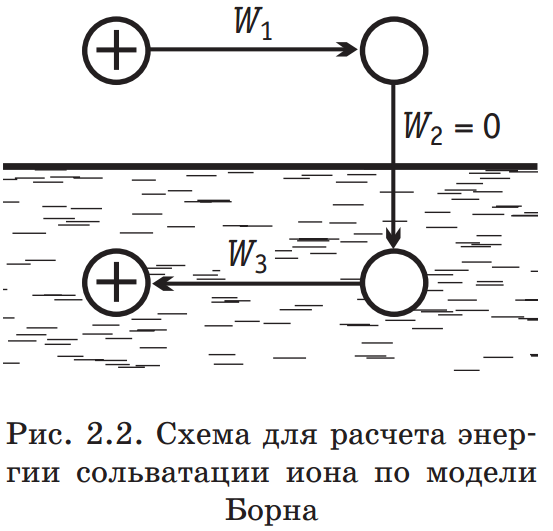
Наиболее простая модель для оценки энергии сольватации была предложена М. Борном. Согласно этой модели, ион рассматривается как заряженный шарик радиуса r_i, а растворитель — как сплошная однородная среда (континуум) с диэлектрической постоянной ε. Процесс переноса заряженного шарика из вакуума в среду разбивается на три этапа: 1) разряд шарика в вакууме; 2) перенос незаряженного шарика из вакуума в растворитель; 3) заряжение шарика в среде (рис. 2.2). При этом предполагается, что работа на втором этапе W₂ = 0, а для расчета работы на этапах 1 и 3 (W₁ и W₃) используются основные законы электростатики. Так, согласно закону Кулона, сила, действующая на каждый из двух зарядов q₁ и q₂ (с учетом знака), находящихся в среде с диэлектрической постоянной ε на расстоянии r, равна:

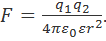(2.3.1)

Поэтому напряженность поля X, т. е. сила, которая действует на заряд +1, находящийся в среде на расстоянии r от заряда q, составляет:

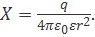(2.3.2)

Поскольку напряженность поля связана с электрическим потенциалом ϕ общей формулой 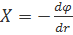, то для потенциала на поверхности сферы радиуса r_i получаем:

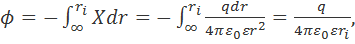(2.3.3)

где нижний предел интегрирования соответствует выбору нулевого потенциала на бесконечно большом расстоянии от рассматриваемой сферы. Из уравнения (2.3.3) вытекает следующая формула для работы заряжения сферы:

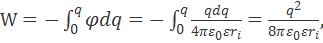(2.3.4)

В соответствии с формулой (2.3.4), для работ W₁ и W₃ получаем выражения

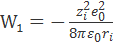и ,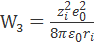

где z_ie₀ - заряд иона.

Учитывая, что свободная энергия сольватации ,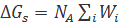

выводим основную формулу модели Борна:

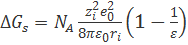. (2.3.5)

Если воспользоваться уравнением Гиббса—Гельмгольца, согласно которому

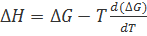, (2.3.6)

то из уравнения (2.3.5) можно получить также выражение для энтальпии сольватации:

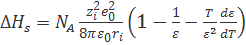- , (2.3.7)

Уравнение (2.3.7) называют уравнением Борна—Бьеррума.

Энергии гидратации, рассчитанные по модели Борна, весьма значительны и достаточны для разрушения кристаллической решетки при образовании растворов электролитов. Этот наиболее важный качественный вывод из теории Борна показывает, что основной причиной образования и устойчивости растворов электролитов служит сольватация ионов. К этому выводу можно прийти также, не производя расчетов, а сопоставляя формулы (2.2.6) и (2.3.5). Если в этих формулах пренебречь 1/n и 1/ε по сравнению с единицей, положить z₁=z₂, то энергия сольватации одного иона окажется равной половине энергии кристаллической решетки. Иначе говоря, энергия сольватации двух ионов - катиона и аниона - как раз скомпенсирует энергию разрушения решетки кристалла.

Для количественной проверки теории сольватации Борна удобно воспользоваться следующим приемом. Сложим энтальпии гидратации катиона и аниона и сравним полученную величину с тепловым эффектом сольватации соответствующей соли, вычисленным из термодинамического цикла. Например, для хлорида натрия

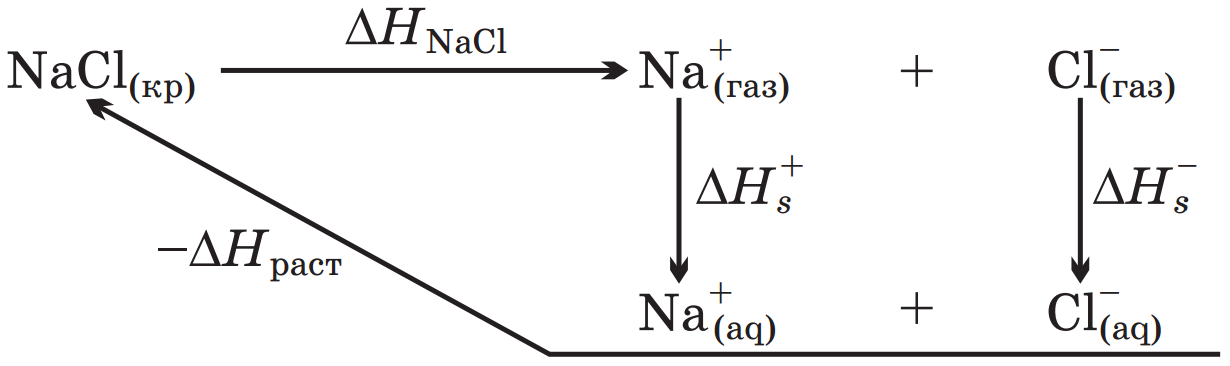
Где ∆H_раст – тепловой эффект растворения, экстраполированный на бесконечно разбавленный раствор соли.

Из этого цикла для теплового эффекта сольватации хлорида натрия получаем:

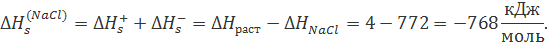
Аналогичным способом можно рассчитать ∆Hs и для другихсолей.

Рассчитанные по Борну величины ∆Hs (соли) значительно превышают соответствующие экспериментальные значения. Это указывает на весьма приближенный характер допущений, положенных в основу модели Борна. Поэтому были предприняты неоднократные попытки уточнить теорию сольватации Борна (Бернал и Фаулер; Уэбб; ван-Аркель и де-Бур; Эли и Эванс; Фрэнк и Венн и др.). Некоторые из них проводились в рамках все того же континуального подхода (например, поправки на уменьшение диэлектрической постоянной растворителя вблизи иона за счет более жесткой ориентации диполей в поле иона, а также учет работы сжатия растворителя при введении в него электролита — эффекта электрострикции). Предлагались также поправки, основанные на учете реальных микроскопических свойств дипольных жидкостей, например тетраэдрической структуры воды и энергии ее разрушения в ходе сольватации. Детализация микроскопического строения растворов, развитие молекулярно-статистических теорий и расчетных методов позволяют в настоящее время использовать значительно более сложные модели и во многих случаях устранить различия между рассчитанными и экспериментальными значениями ∆Hs (соли). Однако при детальной проверке этих моделей встает задача экспериментального определения энергии сольватации отдельного иона, так как при суммировании рассчитанных величин ∆Hs⁺ и ∆Hs⁻ ошибки, обусловленные недостатками моделей, могут скомпенсироваться.