Теория и расчет центробежных форсунок

Камеры сгорания ГТД работают на жидких углеводородных топливах, для распыливания которых обычно применяются форсунки центробежного типа. В камеру закручивания центробежной форсунки (рис.4.12) топливо вводится несколькими тангенциальными отверстиями 2, что вызывает его вращение в камере 1. При выходе струи из сопла 3 действие центростреми­тельных сил со стороны стенок прекращается и частицы жид­кости разлетаются по прямолинейным лучам, касательным к их прежним траекториям - цилиндрическим поверхностям, соосным с соплом. Если пренебречь трением, то момент количества движения вдоль камеры 1 остается постоянным, как это следует из уравнения моментов количества движения:

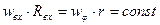(4.26)

Давление в потоке жидкости при отсутствии потерь определится из уравнения Бернулли:

,

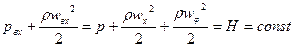где H – полный напор. Из уравнения Бернулли следует:

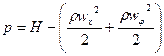(4.27)

Рис.4.12. Схема одноканальной центробежной форсунки. 1 – камера закручивания, 2 – тангенциальные каналы, 3 – сопло, 4 – воздушный вихрь

Из уравнения (4.26) следует, что при приближе­нии к оси форсунки скорость должна стремиться к беско­нечно большой величине. Тогда давление р должно стремиться к бес конечно большой отрицательной величине, что физически не­возможно. В действительности при приближении к оси форсунки давление падает до тех пор, пока не сравняется с атмосферным (давлением окружающей среды). Центральная часть камеры закручивания заполняется воздушным вихрем с ради­усом r_m , а топливо вытекает кольцевой струей с живым сечением

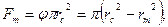где φ – коэффициент живого сечения форсунки.

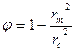(4.28)

Теория центробежной форсунки разработана Г.Н.Абрамовичем.

Из рассмотрения условия равновесия кольцевого элемента в струе в теории доказывается, что осевая скорость w_x остается по радиусу постоянной. Используя это условие можно также показать, что коэффициент расхода идеальной форсунки μ в уравнении объемного расхода является функцией φ и А.

Уравнение объемного расхода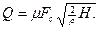

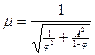(4.29)

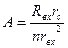, (4.30)

где A – геометрическая характеристика форсунки, n – число тангенциальных каналов (остальные обозначения указаны на рис.4.12.

Для нахождения зависимости между φ и A Г.Н Абрамович выдвигает гипотезу, что в форсунке уста­навливается режим течения, требующий для данного расхода минимального напора. Действительно, расчеты показывают, что как при очень больших, так и при очень малых размерах воз­душного вихря получаются малые значения μ. При большом r_m (малом живом сечении струи) большой напор тратится на получение большого значения скорости w_x. При малом r_m большой напор тратится на создание большой скорости w_φ.

Используя эту гипотезу, берем производную 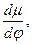приравниванием её к нулю и находим:

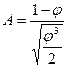(4.31)

Подставляя (4.31) в (4.29), получим окончательно

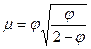(4.32)

и 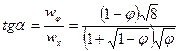(4.33)

Качество распыливания сильно зависит от толщины пелены топлива, вытекающего из форсунки, взятой по нормали к векто­ру скорости w_т (рис 4.12).

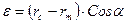(4.34)

Зависимость μ, φ, ε/r_c и телесного угла струи 2α от геометрической характеристики форсунки А приведена на рис. 4.13.

Вытекающая из сопла форсунки пелена неустойчива к воз­действию слабых возмущений (шероховатости стенок, турбулент­ных пульсаций в жидкости и т.д.). На пелене образуются про­дольные и поперечные волны, амплитуды которых быстро растут. С гребней волн срываются мельчайшие капли ,а затем и вся пе­лена распадается на рой капель различных диаметров. Теория распада жидкой струи была разработана Релеем (1878 г.).

Если капля продолжает двигаться по отношению к воздуху, то на её поверхности создается распределение давлений, ко­торое деформирует, сплющивает каплю. При определенном соот­ношении параметров силы аэродинамического давления могут преодолеть силы поверхностного натяжения и произойдет дроб­ление капли. Отношение указанных сил называют критерием дробления, или критерием Вебера

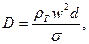(4.35)

где d - диаметр капли, w – скорость капли по отношению к газу с плотностью ρ_г, σ - коэффициент поверхностного натяжения капли.

При значении D = 10,7 дробятся 10 - 20 % капель. При D≥14 достигается верхний предел дробления, когда все 100 % капель дробятся на множество более мелких капель. При движении капли относительно воздуха и ее деформации происходит одновременно ее торможение. Но при уменьшении w уменьшается D и если вначале движения величина D не достигла критического значения, то дробления капли не произойдёт, а её деформация уменьшится. Дробление капель приводит к сильному возрастанию их общей поверхности, что увеличивает скорость испарения топлива и образования свежей смеси.

После завершения процесса дробления в потоке воздуха образуется рой капель различных диаметров. Опытным путем (например, парафиновым методом) можно определить количество и массу капелъ G_i с размерами от 0 до 20 мкм, от 20 до 40 мкм и т.д. Оказывается, что мелких капель в потоке очень много, но их относительная масса g_i = G_i/G_∑ незначительна. По опытным данным строятся спектры распыливания топлива. На рис.4.16 в качестве примера показаны спектры распыливания для форсунки центробежного типа при давлениях распыливания Р_ф= 18 и 4 кг/см² (≈ 1,8 и 0,4 МПа). Мелкость распыливания принято характеризовать средним медианным диаметром d_М, которому со­ответствует 50 % общей массы капель. Чем больше дав­ление распыливания, тем больше начальная скорость капель относительно воздуха и тем меньше d_М. Для данных на рис.4.16 величина d_М будет иметь значения порядка 42 и 76 мкм, соответственно.

Рис.4.13. Зависимость параметров центробежной форсунки

от геометрической характеристики

Рис.4.14. Спектры распыливания топлива форсункой

Используя π -теорему теории подобия и считая, что влияние изменения критериев подобия 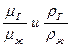мало по сравнению с другими факторами, можно прийти к выводу, что качество распыливания будет определяться двумя безразмер­ными комплексами π₁ и π₂. Излагаемый метод разработан М.С.Волынским.

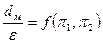, (4.36)

где 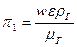- число Re, отнесенное к толщине пелены ε, и

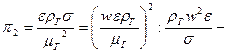отношение квадрата числа Re к критерию Вебера (полагая d ≈ ε), 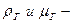плотность и динамическая вязкость газа, соответственно.

Обработка опытных данных позволила, выяснить значение функции в уравнении (4.36) и предложить экспериментальную формулу

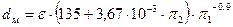(4.37)

Приведенные выше теоретические и полуэмпирические зави­симости позволяют провести приближенный расчет форсунки. Чем меньше вязкость топлива, тем ближе результаты расчё­та к действительности. Секундный расход топлива и ско­рость воздуха в месте установки форсунки известны, значением среднего медианного диаметра задаются. Ве­личина d_м выбирается в зависимости от начальной температу­ры воздуха, испаряемости и других свойств топлива, расстоя­ния от форсунки до зоны горения и может составлять от 30 ÷ 40 до 100 мкм.

В расчете должны быть определены основные геометричес­кие размеры форсунки – r_c, R_вх, r_вх, n и потребный перепад давлений ∆p_ф . Задаваясь углом конуса распыливания 2α, который для камер сгорания ГТД, сообразуясь с углом переходного конуса 2β, выбирают в пределах 90 ÷ 110°, по графику рис. 4. 13 находят А , 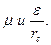Если форсунка устанавливается по потоку, то среднюю на­чальную скорость на выходе из форсунки можно принять рав­ной скорости w_т.

Для форсунки, установленной против потока, скорость движе­ния капли но отношению к воздуху равна геометрической раз­ности векторов скорости истечения w_т и скорости на­бегающего потока w_в, где w_т определяется из уравнения неразрывности

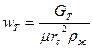(4.38)

Для более простого случая, когда w = w_т, подставляя формулу (4.38) в (4.37), получим:

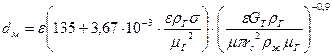
(4.39)

Подставляя в последнее выражение найденное по рис.4.15 значение ε = r_с· f(A), после преобразований получим транс­цендентное уравнение:

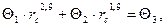(4.40)

где