Приклади розв’язування задач. Приклад 1. Обчислити граничне розведення, межу виявлення, граничну концентрацію і показник чутливості

Приклад 1. Обчислити граничне розведення, межу виявлення, граничну концентрацію і показник чутливості, якщо 0,005мкг речовини калій катіона можна виявити у розчині об’ємом 0,05см³.

Дано:

m_min(К⁺) = 0,005 мкг

V_min(К⁺(р)) = 0,05 см³

V_гран(К⁺(р)) – ?

С_гран(К⁺) – ?

С_min1(К⁺) – ?

pD – ?

Розв’язування

1. Визначення граничного розведення.

V_гран(К⁺(p)) = [V_min(К⁺(p))·10⁶]:m_min(К⁺) = (0,05см³·10⁶мкг/г):0,005мкг = =1·10⁷см³/г

2. Визначення граничної концентрації.

С_гран(К⁺) = 1:V_гран(К⁺(p)) = 1г:1·10⁷см³ = 1:1·10⁷ г/см³

3. Визначення межі виявлення.

С_min1(К⁺) = 1г:1·10⁷см³ = 1·10^–7 г/см³

4. Визначення показника чутливості.

pD = –lgC_min1(К⁺) = –lg1·10^–7 = 7.

Приклад 2. Визначити масу речовини BaCl₂·2H₂O, що викристалізується при охолодженні насиченого при 100°С розчину барій хлориду масою 794г до 10°С, якщо коефіцієнти розчинності його дорівнюють 0,588 при 100°С і 0,357 при 10°С.

Дано:

m(BaCl₂(p)) = 794г М(BaCl₂ ) = 208г/моль

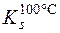= 0,558 M(BaCl₂·2H₂O) = 244г/моль

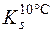= 0,357

m(BaCl₂·2Н₂О) – ?

Розв’язування

1. Визначення маси речовини BaCl₂, що міститься в насиченому при 100°С розчині.

m(BaCl₂) = 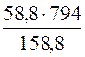= 294г

2. Визначення маси води у розчині, насиченому при 100°С.

m(H₂O) = 794г–294г = 500г

3. Визначення маси речовини BaCl₂·2H₂O, що викристалізується при 10°С. Позначимо масу ВаСl₂·2H₂O, яка викристалізується при 10°С, за x, тобто:

m(BaCl₂·2Н₂О) = x г.

Тоді маса води, що міститься в x г BaCl₂·2Н₂О, дорівнює: m(H₂O) = 36x:244 = 0,1475·х г, а в розчині залишиться (500–0,1475·х)г води.

Маса BaCl₂, яка міститься в х г BaCl₂·2H₂O, дорівнює: m(BaCl₂) = 208х:244 = 0,8525х г, а у розчині залишиться (294–0,8525)г барій хлориду.

Таким чином, є рівність:

У 100г води розчиняється 35,7г BaCl₂,

у (500–0,1475х)г води – (294 – 0,8525х)г BaCl₂.

Тоді (294–0,8525х) = ;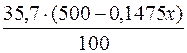

100·(294–0,8525х) = 35,7·(500–0,1475х);

х=144,4; m(BaCl₂·2H₂O) = 144,4г.

Приклад 3. У воді масою 1кг розчинено калій гідроксид масою 560г. Знайти молярні частки речовин калій гідроксиду і води у розчині.

Дано:

m(H₂O) = 1кг М(Н₂О) = 18г/моль

m(KOH) = 560г M(KOH) = 56г/моль

χ(KOH) – ?

χ(H₂O) – ?

Розв’язування

1. Визначення кількості речовини калій гідроксиду в розчині.

n(KOH) = 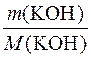= = 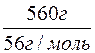10моль

2. Визначення кількості речовини води в розчині.

n(H₂O) = 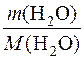= = 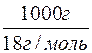55,5 моль.

3. Визначення молярної частки речовини калій гідроксиду в розчині.

χ(KOH) = 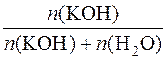= = 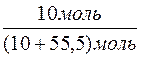0,1530, або 15,30%

4.Визначення молярної частки води в розчині.

χ(H₂O) = 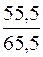= 0,8470 або 84,70%.

Приклад 4. Є розчин фосфатної кислоти з масовою часткою речовини H₃PO₄ 38,17%. Густина розчину становить 1,24г/см³. Розрахувати молярну масу еквівалента речовини H₃PO₄ у розчині, якщо молярна концентрація еквівалента речовини H₃PO₄ у розчині 9,6580 моль/дм³.

Дано:

w(%)(H₃PO₄) = 38,17

ρ(H₃PO₄(p)) = 1,24г/см³

c(f_екв(H₃PO₄)H₃PO₄) = 9,6580 моль/дм³

M(f_екв(H₃PO₄)H₃PO₄) – ?

Розв’язування

1. Визначення молярної маси еквівалента речовини H₃PO₄.

c(f_екв(H₃PO₄) H₃PO₄) =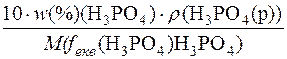

M(f_екв(H₃PO₄) H₃PO₄) _{= =}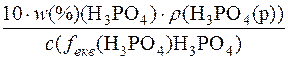

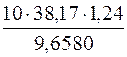_{= =} 49 г/моль

Отже, M(f_екв(H₃PO₄)H₃PO₄) = 49г/моль; М(H₃PO₄) = 98г/моль

Відомо, що M(f_екв(X)X) = f_екв(X)·М(X), тоді M(f_екв(H₃PO₄)H₃PO₄) = = f_екв(H₃PO₄)·М(H₃PO₄)

f_екв(H₃PO₄) = M(f_екв(H₃PO₄)H₃PO₄)/М(H₃PO₄)

f_екв(H₃PO₄) = 49г/моль: 98г/моль = ½

Отже, f_екв(H₃PO₄) = ½. Тоді М(½H₃PO₄) = 49г/моль.

Приклад 5. У воді масою 60г розчинили сульфатну кислоту масою 40г. Використовуючи ці дані, виразити склад розчину і концентрацію H₂SO₄ всіма відомими способами.

1. Масова частка (%) розчиненої речовини в розчині.

Дано:

m(H₂O) = 60г

m(H₂SO₄) = 40г

w(%)(H₂SO₄) – ?

w(%)(H₂SO₄) = m(H₂SO₄):[m(H₂SO₄)+m(H₂O)]·100 =

= 40г:(40г+60г)·100 = 40,00%.

2. Мольна частка (%) розчиненої речовини в розчині.

Дано:

m(H₂O) = 60г M(H₂SO₄) = 98,08г/моль

m(H₂SO₄) = 40г M(H₂O) = 18,02г/моль

χ(%)(H₂SO₄) – ?

χ(%)(H₂SO₄) = n(H₂SO₄):[n(H₂SO₄)+n(H₂O)·100 =

= (40г:98,08г/моль):[40г:98,08г/моль+60г:18,02г/моль]·100 =

= 0,408моль:(0,408моль+3,330моль)·100 = 10,91%.

3. Моляльність розчину (відношення числа молів розчиненої речовини, що припадає на 1кг розчинника).

Дано:

m(H₂O) = 60г

m(H₂SO₄) = 40г

b(H₂SO₄/H₂O) – ?

b(H₂SO₄/H₂O) = n(H₂SO₄):m(H₂O) = [m(H₂SO₄):M(H₂SO₄)]:m(H₂O) =

= (40г:98,08г/моль):0,06кг = 6,797моль/кг.

4. Сольватне число розчиненої речовини в розчині.

Дано:

m(H₂O) = 60г

m(H₂SO₄) = 40г

h(H₂SO₄) – ?

h(H₂SO₄)=n(H₂O):n(H₂SO₄)=

= (1000г:18,02г/моль):(40г/60г·1000г:98,08г/моль)=

= 55,50моль:6,797моль = 8,16.

5. Молярна концентрація розчиненої речовини в розчині.

Дано: m(H2O) = 60г m(H2SO4) = 40г w(%)(H2SO4) = 40,00

З довідника: густина розчину ρ сульфатної кислоти з масовою часткою речовини 40% становить 1,303г/см3

c(H₂SO₄) – ?

c(H₂SO₄) = 10·w(%)(H₂SO₄)·ρ(H₂SO₄(p))/M(H₂SO₄) =

= 10·40,00%·1,303г/см³/98,08г/моль = 5,3140моль/дм³.

6. Молярна концентрація еквівалента речовини H₂SO₄ у розчині за умови, що цей розчин буде використано для реакції сульфатної кислоти, у якій фактор еквівалентності дорівнює ½.

Дано: w(%)(H₂SO₄) = 40,00

m(H₂O) = 60г ρ(H₂SO₄(p)) = 1,303г/см³

m(H₂SO₄) = 40г M(H₂SO₄) = 98,08г/моль

с(½H₂SO₄) – ? M(½H₂SO₄) = 49,04г/моль

с(½H₂SO₄) = 10·w(%)(H₂SO₄)·ρ(H₂SO₄(p))/M(½H₂SO₄) =

= 10·40,00%·1,303г/см³/49,04г/моль = 10,6281моль/дм³.

Приклад 6. До 20см³ розчину аргентум нітрату, с(AgNO₃)=0,40моль/дм³, додали 40см³ розчину калій ціаніду, с(KCN)=0,50моль/дм³. Обчислити рівноважну молярну концентрацію речовини аргентум-іонів у суміші, якщо константа нестійкості аніона [Ag(CN)₂]⁻ становить 1,0·10^–21.

Дано:

V(AgNO₃) = 20см³

с(AgNO₃) = 0,40моль/дм³

V(KCN) = 40см³

с(KCN) = 0,50моль/дм³

K_н[Ag(CN)₂]^– = 1,0·10^–21

[Ag⁺] – ?

Розв’язування

Визначаються молярні концентрації кожної речовини після змішування розчинів.

Загальний об’єм суміші після змішування становить 60см³.

с(AgNO₃) = (0,40·20)/60 = 0,13моль/дм³ ; с(Ag⁺) = 0,13моль/дм³.

с(KCN) = (0,50·40)/60 = 0,33моль/дм³ ; с(CN^–) = 0,33моль/дм³.

Молярна концентрація речовини калій ціаніду по відношенню до молярної концентрації аргентум нітрату є в надлишку, тому у розчині може відбуватися процес комплексоутворення:

Ag⁺ + 2CN^– D [Ag(CN)₂]^–.

Цей процес зворотний, який кількісно можна охарактеризувати константою нестійкості комплексного йона.

Визначаємо рівноважну концентрацію Ag⁺ у суміші.

[Ag(CN)₂]^– D Ag⁺ + 2CN^–

	1моль	1моль	2моль
срівн.		х моль	2х моль

K_н[Ag(CN)₂]^– =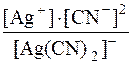

[Ag⁺] = х моль;

[CN^–]=с(CN^–)–2(с(Ag⁺)–х);

[CN^–] = 0,33–2·(0,13–х) = 0,33–2–0,13 = 0,07моль/дм³;

[Ag(CN)₂]^– = с(Ag⁺)–х = (0,13–х)моль/дм³.

Оскільки х – мала величина у порівнянні з молярною концентрацією Ag⁺, то значенням х можна знехтувати.

1,0·10^–21 = 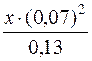; х= 2,65·10^–20.

Рівноважна концентрація аргентум-іонів у розчині

[Ag⁺]=2,65·10^–20моль/дм³.

Приклад 7. Молярна концентрація речовини Н⁺-іонів у розчині ацетатної кислоти (с(СН₃ООН)=0,1моль/дм³) становить 1,3·10^–3 моль/дм³.Обчислити константу і ступінь дисоціації кислоти.

Дано:

с(СН₃СООН) = 0,1моль/дм³

[H⁺] = 1,3·10^–3моль/дм³

K_д(CH₃COOH) – ?

α – ?

Розв’язування

CH₃COOH D H⁺ + CH₃COO^–

У стані рівноваги [H⁺] = [CH₃COO^–]= с·α; a[CH₃COOH] = с–с·α

K_д(CH₃COOH) = 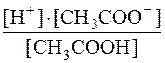= =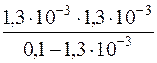1,71·10^–5

K_д(CH₃COOH) = α²·с(CH₃COOH); α= 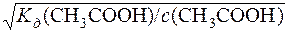= = 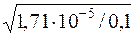0,0171 (1,71%).

Приклад 8. Розрахувати активність натрій-іонів і сульфат-іонів у розчині, в 1дм³ якого міститься 0,005 натрій сульфату і 0,02моль ацетатної кислоти.

Дано:

с(Na₂SO₄) = 0,005моль/дм³

с(СH₃COOH) = 0,02моль/дм³

а(Na⁺) – ?

a( ) – ?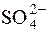

Розв’язування

Визначаються молярні концентрації Na⁺ і 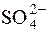у розчині.

Na₂SO₄ " 2Na⁺ +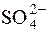

	1моль	2моль	1моль
срівн.		(0,005·2) моль	0,005 моль

[Na⁺] = 0,01моль/дм³; [ 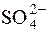] = 0,005моль/дм³.

Дисоціацією молекул ацетатної кислоти нехтують, оскільки ацетатна кислота – слабкий електроліт і участь її у створенні йонної сили не суттєва.

Розраховують йонну силу розчину.

μ = 3с(Na₂SO₄) = 3·0,005 = 0,015моль/дм³.

Коефіцієнт активності йонів Na⁺ за цієї йонної сили f(Na⁺)=0,89, a йонів 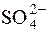– f( 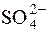) = 0,63 (з довідника).

Далі розраховують активності йонів Na⁺ і 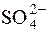у розчині.

а(Na⁺) = [Na⁺]·f(Na⁺) = 0,01· 0,89 = 8,9·10^–3моль/дм³;

а( 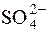) = [ 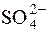]·f( 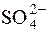) = 0,005·0,63 = 3,15·10^–3моль/дм³.

Приклад 9. Розрахувати ступінь дисоціації і pH у розчині ацетатної кислоти (с(СН₃СООН) = 0,2моль/дм³) з урахуванням коефіцієнтів активності.

Дано:

с(СН₃СООН) = 0,2моль/дм³ K_д(СH₃COOH) = 1,74·10^–5. (μ=0)

α – ?; рН - ?

Розв’язування

Визначають наближену молярну концентрацію йонів Н⁺ у розчині.

СН₃СООН D Н⁺ + СН₃СОО^–

	1моль	1моль	1моль
срівн.	(с–сα)моль	(сα)моль	(сα)моль

[H⁺] = [СН₃СОО^–]

Оскільки ступінь дисоціації – мала величина, то допускають, що рівноважна концентрація СН₃СООН дорівнює початковій молярній концентрації ацетатної кислоти, тобто [СН₃СООH] = с(СН₃СООН).

[H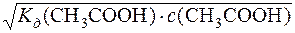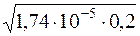⁺] = = = 1,87·10^–3

[H⁺] = 1,87·10^–3моль/дм³.

Далі визначають йонну силу розчину.

Оцтова кислота – бінарний електроліт, тому

[H⁺] = [СН₃СОО^–] = 1,87·10^–3 моль/дм³ і μ=1,87·10^–3.

За рівнянням Девіса визначають точне значення константи дисоціації СН₃СООН.

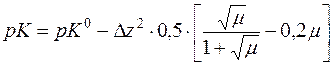
Δz² = Σnz² продуктів реакції – Σmz² вихідних речовин = 1+1–0=2

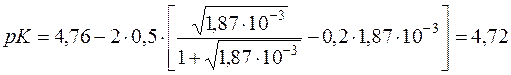
K_д(СH₃COOH) = 1,92·10^–5.

Визначають молярну концентрацію йонів H⁺ з урахуванням активності.

[H⁺]а= 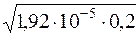= 1,96·10^–3.

[H⁺]а = 1,96·10^–3 моль/дм³.

Далі визначають р_аН розчину і ступінь дисоціації CH₃COOH.

р_аH = –lg[H⁺]a = –lg1,96·10^–3 = 2,71

α = 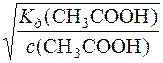= = 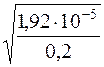9,8·10^–3 або 0,98%

р_аН = 2,71

α = 0,98%

Приклад 10. Як зміниться pH і ступінь дисоціації амоній гідроксиду у розчині з с(NH₃·H₂O)=1,0моль/дм³ після додавання до розчину речовини амоній хлориду в такій кількості, щоб молярна концентрація речовини амоній хлориду в розчині стала 0,2моль/дм³?

Дано:

с(NH₃·H₂O) = 1,0моль/дм³ K_д(NH₃·H₂O) = 1,76·10^–5

с(NH₄Cl) = 0,2моль/дм³

pH₁ – ? α₁ – ?

pH₂ – ? α₂ – ?

Розв’язування

Визначення молярної концентрації гідроксид-іонів у розчині NH₃·H₂O до додавання солі:

[OH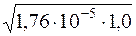^–] = = 4,20·10^–3моль/дм³.

Визначення ступеня дисоціації амоній-гідроксиду:

α = (4,20·10^–3/1,0)·100 = 0,42%

Визначення pOH розчину:

pOH = –lg4,20·10^–3 = 2,38

Визначення pH розчину:

pH = 14–pOH = 14–2,38 = 11,62

Визначення молярної концентрації гідроксид-іонів у розчині після додавання солі NH₄Cl:

[OH^–] = 1,76·10^–5·1,0/0,2 = 8,8·10^–5моль/дм³

Визначення ступеня дисоціації амоній гідроксиду після додавання солі NH₄Cl:

α = (8,8·10^–5/1,0)·100 = 0,009%

Визначення pOH розчину після додавання солі NH₄Cl:

pOH = –lg8,8·10^–5 = 4,06

Визначення pH розчину після додавання солі NH₄Cl:

pH = 14–pOH = 14–4,06 = 9,94

Після додавання до 1,0М розчину амоній гідроксиду амоній хлориду pH зміниться з 11,62 до 9,94, а ступінь дисоціації зменшиться з 0,42% до 0,009%.

Приклад 11. Розрахувати, як зміниться pH, якщо до 400см³ буферного розчину з молярними концентраціями амоній гідроксиду 0,2моль/дм³ і амоній хлориду 0,3моль/дм³ додати 100см³ розчину NaOH з молярною концентрацією натрій гідроксиду 0,05моль/дм³.

Дано:

V(NH₃·H₂O+NH₄Cl) = 400cм³ K_д(NH₃·H₂O) = 1,76·10^–5

с(NH₃·H₂O) = 0,2моль/дм³

с(NH₄Cl) = 0,3моль/дм³

V(NaOH) = 100см³

с(NaOH) = 0,05моль/дм³

ΔpH – ?

Розв’язування

Допускають, що [NH₃·H₂O] ≈ с(NH₃·H₂O) = 0,2моль/дм³; [NH₄Cl] ≈ с(NH₄Cl) = 0,3моль/дм³.

Визначають молярну концентрацію гідроксид-іонів у буферному розчині:

[OH^–] = K_д(NH₃·H₂O)· 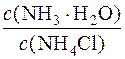= 1,76·10^–5· 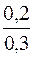= 1,7·10^–5моль/дм³

Визначають pOH і pH буферної системи:

pOH = –lg[OH^–] = 1,7·10^–5 = 4,93; pH = 14–pOH = 14–4,93 = 9,07.

Додавання розчину натрій гідроксиду викликає перетворення частини амоній-іонів в амоніак.

Визначають молярні концентрації амоніаку і амоній хлориду у розчині після додавання натрій гідроксиду:

с(NH₃·H₂O) = 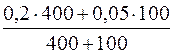= 0,17моль/дм³

с(NH₄Cl) = 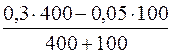= 0,23моль/дм³

Визначають молярну концентрацію гідроксид-іонів у буферному розчині після додавання розчину натрій гідроксиду:

[OH^–] = K_д(NH₃·H₂O)· 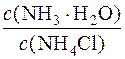= 1,76·10^–5· 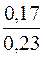= 1,3·10^–5моль/дм³

Визначають pOH і pH буферної системи після додавання розчину лугу:

pOH = –lg[OH^–] = –lg1,3·10^–5 = 4,87;

pH = 14–pOH = 14–4,87 = 9,13.

При додаванні лугу ∆pH = 9,13–9,07 = 0,06.

Тобто, при додаванні до буферних систем невеликих кількостей сильних основ або сильних кислот pH буферної системи змінюється в дуже незначній мірі.

Приклад 12. Обчислити, у скільки разів розчинність (моль/дм³) барій сульфату в насиченому водному розчині більша, ніж у водному розчині натрій сульфату з концентрацією Na₂SO₄ 0,05моль/дм³

Дано:

BaSO₄, с(Na₂SO₄)=0,05моль/дм³ ДР(BaSO₄) = 1,1·10^–10

– ?

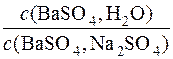Розв’язування

У насиченому водному розчині встановлюється рівновага:

BaSO₄ D Ba²⁺ +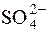

		1моль	1моль
срівн.		х моль	х моль

ДР(BaSO₄) = [Ba²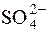⁺]·[ ]; 1,1·10^–10 = x²; x=1,05·10^–5.

[Ba²⁺] = с(BaSO₄). Отже, с(BaSO₄, H₂O) = 1,05·10^–5моль/дм³.

Далі визначається молярна концентрація 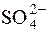-іонів у розчині натрій сульфату з с(Na₂SO₄)=0,05моль/дм³:

Na₂SO₄ " 2Na⁺ +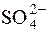

	1моль	2моль	1моль
срівн.			0,05 моль

Отже, с( 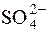) = 0,05моль/дм³.

Визначається розчинність барій сульфату у розчині натрій сульфату з с(Na₂SO₄)=0,05моль/дм³:

BaSO₄ D Ba²⁺ +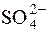

		1моль	1моль
срівн.		х моль	(х+0,05) моль

ДР(BaSO₄) = [Ba²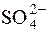⁺]·[ ]; 1,1·10^–10 = х·(х+0,05)

Оскільки величина х у загальній рівноважній молярній концентрації сульфат-іонів у порівнянні з 0,05моль мала, то нею можна знехтувати і вважати, що рівноважна молярна концентрація сульфат-іонів дорівнює 0,05моль/дм³. Тоді:

1,1·10^–10 = х·0,05; х = 2,2·10^–9.

Отже, с(BaSO₄, Na₂SO₄) = 2,2·10^–9моль/дм³

Далі визначається , у скільки разів молярна концентрація барій сульфату у насиченому водному розчині більша, ніж у водному розчині натрій сульфату з с(Na₂SO₄)=0,05 моль/дм³.

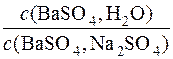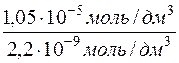= = 4772

Відповідь: у 4772 рази розчинність барій сульфату у воді більша, ніж у водному розчині Na₂SO₄ з с(Na₂SO₄) = 0,05моль/дм³.

Приклад 13. Обчислити розчинність аргентум сульфіду у розчині хлоридної кислоти (с(НСl)=0,1моль/дм³), насиченому гідроген сульфідом (с(H₂S)=0,1моль/дм³).

Дано:

Ag₂S ДР(Ag₂S) =6,3 · 10^–50;

с(HCl) = 0,1моль/дм³ 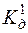(H₂S) = 1,0·10^–7;

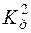с(H₂S) = 0,1моль/дм³ (H₂S) = 2,5·10^–13.

S(Ag₂S) – ?

Розв’язування

Визначають молярну концентрацію Н⁺-іонів у розчині хлоридної кислоти:

[H⁺] = с(HCl) = 0,1моль/дм³.

Визначають частку речовини вільних сульфід-іонів у розчині. Процес розчинення Ag₂S в HCl можна представити таким рівнянням:

Ag₂S(т) D 2Ag⁺ + S^2–

S^2– + 2H⁺ D H₂S

Або Ag₂S_(т) + 2Н⁺ D 2Ag⁺ + H₂S

с(S^2–) = [H₂S] + [HS^–] + [S^2–]

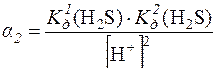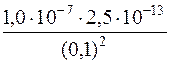= = 2,5∙10^–18

[S^2–] = с(H₂S)∙α₂ = 0,1∙2,5∙10^–18 = 2,5∙10^–19моль/дм³

Розраховують розчинність аргентум сульфіду.

Якщо S – розчинність Ag₂S, то [Ag⁺]=2S

Тоді (2S)²∙0,1 = ДР(Ag₂S)/α₂ = 6,3∙10^–50/2,5∙10^–19 = 2,52∙10^–31

S = 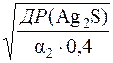= = 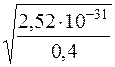2,51∙10^–16

S(Ag₂S) = 2,51∙10^–16моль/дм³.

Приклад 14. Обчисліть pH у водному розчині натрій ацетату з молярною концентрацією CH₃COONa 0,01моль/дм³ за температури 25^oС.

Дано:

с(СН₃COONa) = 0,01моль/дм³ Константа дисоціації оцтової

кислоти –

t° = 25°С K_д(CH₃COOH) =1,74∙10^–5

pH – ? Йонний добуток води за вказаної

температури K_w=1∙10^–14

Розв’язування

Натрій ацетат гідролізується за аніоном.

CH₃COO^– + HOH D CH₃COOH + OH^–

Визначають константу гідролізу ацетат-іона:

K_г(CH₃COO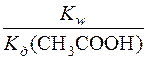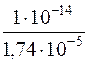^–) = = = 5,7 ∙ 10^–10

Визначають молярну концентрацію Н⁺-іонів у розчині:

[H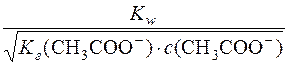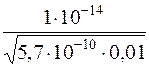⁺] = = = 4,2 ∙ 10^–9 моль/дм³

Визначають pH розчину:

pH = –lg[H⁺] = –lg4,2∙10^–9 = 8,38.

Приклад 15. Яка маса калій ціаніду розчинена у 10см³ водного розчину його, якщо pH розчину становить 11,10?

Дано:

V(KCN) = 10см³ K_д(HCN) = 6,2∙10^–10

pH = 11,10

m(KCN) – ?

Розв’язування

Калій ціанід гідролізується за аніоном.

CN^– + HOH D HCN + OH^–

Визначають молярну концентрацію калій ціаніду в розчині.

pH = 7–½lg K_д(HCN)+½lgс(KCN);

½lgс(KCN) = pH–(7–½lgK_д(HCN)) = pH–7+½lgK_д(HCN);

lgс(KCN) = 2(pH–7+½lgK_д(HCN));

lgс(KCN) = 2[11,10–7+½(–9,19)] = 2∙(–0,495) = –0,99

с(KCN) = 0,1026моль/дм³

Далі визначають масу речовини калій ціаніду, що міститься в 10 см³ цього розчину.

m(KCN) = [M(KCN)∙с(KCN)∙V(KCN)]/1000;

m(KCN) = 65,12г/моль∙0,1026моль/дм³∙0,010дм³/1000 = 0,0668г

m(KCN) = 0,0668г.

Приклад 16. Обчислити константу і ступінь дисоціації форміатної кислоти у водному розчині амоній форміату з молярною концентрацією HCOONH₄ 0,1моль/дм³, який має pH 6,50.

Дано:

с(HCOONH₄) = 0,1моль/дм³

pH = 6,50

K_д(HCOOH) – ?

α – ?

Розв’язування.

Амоній форміат гідролізується і за катіоном, і за аніоном.

HCOO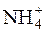^– + + HOH D HCOOH + NH₃∙H₂O

Визначають константу дисоціації форміатної кислоти:

pH = ½pK_w + ½pK(HCOOH) – ½pK(NH₃∙H₂O);

½pK(HCOOH) = pH–½pK_w + ½pK(NH₃∙H₂O);

pK(HCOOH) = 2∙(pH–½pK_w + ½pK(NH₃∙H₂O) = 2∙(6,50–7+2,38) = –3,76

K_д(HCOOH) = 1,74∙10^–4

Визначають ступінь дисоціації форміатної кислоти:

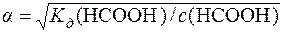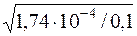= =0,0417 або 4,17%.

Приклад 17. Визначити напрям окисно-відновної реакції 2Fe³⁺+Sn²⁺=2Fe²⁺+Sn⁴⁺, якщо концентрації компонентів дорівнюють: с(Fe³⁺)=с(Sn²⁺)=0,001моль/дм³, с(Fe²⁺)=с(Sn⁴⁺)=0,1моль/дм³.

Розв’язування

За рівнянням Нернста редокс-потенциал системи визначається:

;

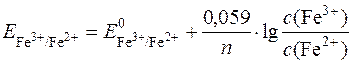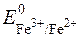= +0,771B (табличне значення).

;

;

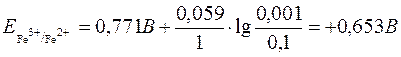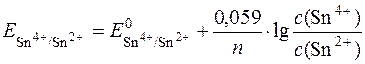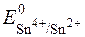= + 0,15B (табличне значення).

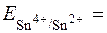0,15B ;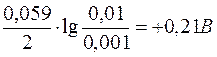

Редокс-пара з більшим окисно-відновним потенціалом є окисником по відношенню до редокс-пари з меншим окисно-відновним потенціалом.

Отже, в даній окисно-відновній реакції окисником є Fe³⁺, а відновником Sn²⁺. Реакція буде проходити в бік утворення Sn⁴⁺ і Fe²⁺.

Електрорушійна сила = Е_ox–E_red = 0,653–0,21 = 0,443B > 0.

Приклад 18. До розчину CuSO₄ з молярною концентрацією купрум сульфату 0,2моль/дм³ додали рівний об’єм розчину амоніаку з c(NH₃)=2,0моль/дм³.

Обчислити молярну концентрацію Сu²⁺ в отриманому розчині, якщо вважати, що у розчині утворюється комплексний катіон [Cu(NH₃)₄]²⁺.

Дано:

c(CuSO₄) = 0,2моль/дм³ Константа нестійкості комплексного

йона

V(CuSO₄(p)) = V(NH₃(p)) K_н[Cu(NH₃)₄]²⁺ = 9,33·10^–13.

c(NH₃) = 2моль/дм³

[Cu²⁺] – ?

Розв’язування.

Визначають вихідні молярні концентрації кожної речовини після змішування розчинів.

с(CuSO₄)=0,1моль/дм³; с(NH₃)=1моль/дм³.

Визначають молярну концентрацію Cu²⁺-іона у розчині після додавання розчину амоніаку.

При додаванні розчину амоніаку концентрація Cu²⁺-іонів зменшується внаслідок реакції комплексоутворення:

Cu²⁺ + 4NH₃ D [Cu(NH₃)₄]²⁺

1моль

4моль

Утворений комплексний йон [Cu(NH₃)₄]²⁺ дисоціює як слабкий електроліт:

[Cu(NH₃)₄]²⁺ D Cu²⁺ + 4NH₃

		1моль	4моль
срівн.	(0,1–х) моль	х моль	(0,6–4х) моль

Оскільки рівноважна молярна концентрація речовини [Сu(NH₃)₄]²⁺-іона дорівнює (0,1–x) моль/дм³, то молярна концентрація речовини амоніаку при утворенні цього комплексу зменшилась на 4(0,1–x)моль/дм³. Тоді рівноважна молярна концентрація амоніаку дорівнює [1–4·(0,1–x)] моль/дм³.

K_н[Cu(NH₃)₄]²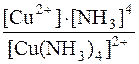⁺= ; 9,33·10^–13 =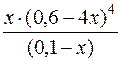

Значення x – мала величина у порівнянні з 0,1 і 0,6, тому значенням x у знаменнику і (4x)⁴ у чисельнику можна знехтувати. Тоді матимемо:

9,33 · 10^–13 = 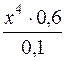; x = 7,2·10^–14.

Отже, [Cu²⁺] у розчині комплексної сполуки [Cu(NH₃)₄]SO₄ становить 7,2 ·10^–14моль/дм³, що свідчить про високу стійкість комплексного катіона.