Структурно-механические свойства дисперсных систем

Возникновение структур и их характер обычно определяют, измеряя механические свойства систем: вязкость, упругость, пластичность, прочность. Поскольку эти свойства связаны со структурой, их называют структурно–механическими.

Структурно–механические свойства систем исследуют методами реологии.

Реология – наука о деформациях и течении материальных систем. Она изучает механические свойства систем по проявлению деформации под действием внешних напряжений.

Термин деформация означает относительное смещение точек системы, при котором не нарушается ее сплошность.

Внешнее напряжение – есть не что иное, как давление Р.

В механике сплошных сред доказывается, что в случае несжимаемых материалов, каковыми являются большинство дисперсных систем, все виды деформации (растяжение, сжатие, кручение и др.) можно свести к основной – деформации сдвига под действием напряжения сдвига Р (Н/м² =. Па). Скорость деформации является скоростью сдвига. Деформацию выражают обычно посредством безразмерных величин 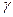. Скорость деформации – 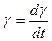, где t – время.

Изучая структурно–механические свойства дисперсных систем, можно определить, образуется ли в системе структура и каков ее характер.

СВОБОДНОДИСПЕРСНЫЕ (БЕССТРУКТУРНЫЕ) СИСТЕМЫ

Агрегативно устойчивые золи (бесструктурные системы) подчиняются законам Ньютона, Пуазейля и Эйнштейна.

Закон Ньютона устанавливает связь между скоростью деформации и напряжением сдвига:

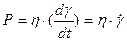(11.1)

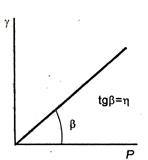
Рис.11.2. Зависимость скорости деформации от напряжения сдвига

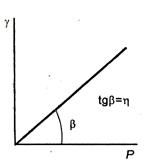
Рис.11.3. Зависимость расхода жидкости от давления

Рис. 11.4. Зависимость вязкости дисперсной системы от концентрации

где Р – напряжение сдвига, поддерживающее течение жидкости, Па; 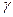– деформация (течение) жидкости; 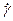– скорость деформации; 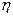– коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью, Па –с; 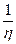– величина, обратная вязкости, называется текучестью.

Уравнение (11.1) представляет собой уравнение прямой, представленной на рис. 11.2.

Вязкость 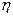– величина постоянная, не зависящая от Р.

Закон Пуазейля выражает зависимость объема жидкости, протекающей через трубу или капилляр, от давления:

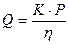, (11.2)

где Q – расход жидкости в единицу времени; Р — давление в трубе; К – константа, определяемая геометрическими параметрами трубы или капилляра 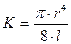,(r и l – радиус и длина трубы). Из графика, отвечающего закону Пуазейля (рис. 11.3), видно, что динамическая вязкость не зависит от давления, а скорость течения жидкости прямо пропорциональна давлению.

Закон Эйнштейна устанавливает зависимость вязкости 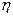бесструктурной жидкой дисперсной системы от концентрации дисперсной фазы:

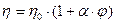(11.3)

где 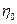– динамическая вязкость дисперсионной среды; 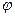– объемная концентрация дисперсной фазы; 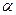–коэффициент, определяемый формой частиц дисперсной фазы. График, отвечающий закону Эйнштейна, дан на рис. 11.4.

Таким образом, относительное приращение вязкости прямо пропорционально относительному содержанию дисперсной фазы. Чем больше 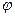, тем сильнее выражено тормозящее влияние частиц, тем больше вязкость. Расчеты, проведенные Эйнштейном, показали, что для сферических частиц 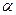= 2,5, для частиц другой формы 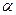> 2,5. Жидкости, подчиняющиеся рассмотренным законам, называются ньютоновыми жидкостями.

ЖИДКООБРАЗНЫЕ СТРУКТУРИРОВАННЫЕ СИСТЕМЫ

При наличии структуры взаимодействием между частицами дисперсной фазы нельзя пренебречь. Прилагаемое напряжение сдвига не только заставляет жидкость течь, но и может разрушать существующую в ней структуру. Это неизбежно должно приводить к нарушению пропорциональности между прилагаемым напряжением Р и скоростью деформации 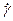, вязкость системы 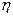становится величиной, зависящей от Р. Следовательно, для таких жидкостей законы Ньютона, Пуазейля и Эйнштейна не выполняются. Такие жидкости называются неньютоновыми жидкостями.

Для описания связи между скоростью деформации 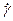и прилагаемым напряжением сдвига Р обычно используют эмпирическое уравнение Оствальда –Вейля:

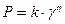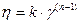или , (11.4)

где k и n – постоянные, характеризующие данную жидкообразную систему.

При n – 1 и k = 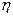уравнение (11.4) превратится в уравнение Ньютона. Таким образом, отклонение величины n от единицы характеризует степень отклонения свойств неныотоновых жидкостей от ньютоновых. При n < 1 ньютоновская вязкость уменьшается с увеличением напряжения и скорости сдвига. Такие жидкости называются псевдопластическими.

При n > 1 ньютоновская вязкость жидкости увеличивается при увеличении напряжения и скорости сдвига. Такие жидкости называются дилатантными.

На рис. 11.5 представлена кривая течения псевдопластической жидкости. На кривой имеются три характерных участка. На участке I (OA) система ведет себя подобно ньютоновой жидкости с большой вязкостью 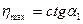.Такое поведение системы объясняется тем, что при малых скоростях течения структура, разрушаемая приложенной нагрузкой, успевает восстанавливаться. Такое течение называется ползучестью.

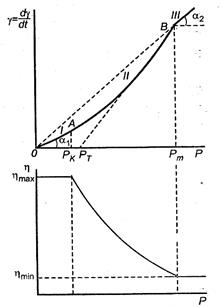
Рис.11.5. Кривая течения псевдопластической структурированной

жидкообразной системы

Ползучесть – это медленное течение с постоянной вязкостью без прогрессирующего разрушения структуры.

Для слабоструктурированных систем участок I обычно небольшой и его практически невозможно обнаружить. Для сильноструктурированных систем область значений Р, при которых наблюдается ползучесть, может быть весьма значительной. Напряжение Р_к соответствует началу разрушения структуры.

На участке II (АВ) зависимость 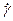от Р теряет линейный характер, при этом вязкость уменьшается. Это уменьшение связано с разрушением структуры. В точке В структура практически полностью разрушена. Напряжение, отвечающее этой точке, называется предельным напряжением сдвига Р_m. При напряжениях Р > Р_m, когда струк­тура системы разрушена, система течет подобно ньютоновой жидкости, имеющей вязкость .

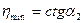Напряжение Р_т называется пределом текучести – это минимальное напряжение сдвига, при котором ползучесть системы переходит в течение. Чем прочнее структура, тем выше предел текучести. Расход жидкости в единицу времени Q, протекающей через трубу при Р < Р_m можно рассчитать по уравнению Бингама:

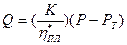(11.5)

где 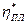– пластическая вязкость, она характеризует способность структуры к разрушению при изменении нагрузки, т. е. 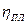= f(Р).

Прочность структуры оценивается не только пределом текучести, но и разностью 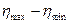. Чем больше эта разность, тем прочнее структура. Значения 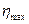и и 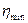могут различаться на несколько порядков. Так, для суспензии бентонитовой глины 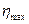= 10⁶ Па * с, a 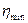= 10^-2 Па * с.

ТВЕРДООБРАЗНЫЕ СТРУКТУРИРОВАННЫЕ СИСТЕМЫ

На рис. 11.6 изображена кривая течения твердообразной структурированной системы. Сравнивая эту кривую с аналогичной кривой для жидкообразной структурированной системы (см. рис. 11.5), видим, что на первой кривой появился горизонтальный участок IV, совпадающий с осью абсцисс. Он заканчивается при достижении давления, равного PS, называемого статическим предельным напряжением сдвига. При Р < PS система не только не течет, но и не проявляет свойств ползучести, 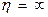. Величина PS характеризует прочность сплошной пространственной сетки.

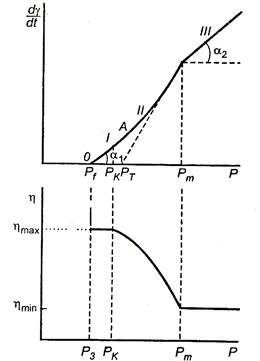
Рис.11.6. Кривая течения твердообразной структурированной системы

При Р > PS кривая течения твердообразной системы аналогична кривой течения жидкообразной системы, рассмотренной выше.

Для твердообразных упругопластичных тел 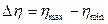на много порядков больше, чем для жидкообразных и при достижении предела текучести Р_Т наступает лавинообразное разрушение структуры с последующим пластическим течением.

В упругохрупких телах течение не наблюдается, так как напряжение, при котором происходит хрупкий разрыв, достигается раньше, чем предел текучести.

ЗАКЛЮЧЕНИЕ

Свойства дисперсных систем зависят от концентрации частиц дисперсной фазы. В разбавленных золях расстояния между частицами сравнительно велики и взаимодействием между ними можно пренебречь. Такие системы являются свободнодисперсными (бесструктурными).

При увеличении концентрации дисперсной фазы между частицами возникают контакты, образуется структура.

Структурированные коллоидные системы делятся на коагуляционные и конденсационно-кристаллизационные. Коагуляционные структуры – гели, в которых частицы дисперсной фазы разделены прослойками дисперсионной среды, образуются за счет ван–дер–ваальсовых сил и обладают малой прочностью. Для этих структур характерны свойства тиксотропии и синерезиса. При определенных условиях гели могут превращаться в золи.

Конденсационно–кристаллизационные структуры образуются за счет непосредственного химического взаимодействия между частицами, характерны для связнодиспересных систем с твердой дисперсионной средой и придают им твердость и хрупкость. Превращение коагуляционных структур в конденсационно–кристаллизационные является процессом необратимым.

Структурированные системы обладают способностью деформироваться под влиянием механических нагрузок, а в некоторых случаях происходит их течение. Изучение таких систем с целью выявления наличия структуры и ее характера осуществляется методами реологии – науки о деформациях и течении материальных систем.

Бесструктурные системы, жидкообразные коагуляционные и твердообразные системы различаются по структурно-механическим свойствам (вязкости, упругости, прочности и пластичности).

Бесструктурные коллоидные системы, подобно чистым жидкостям, подчиняются законам Ньютона, Пуазейля и Эйнштейна. Они обладают постоянной вязкостью, не зависящей от приложенных нагрузок. Они называются ньютоновыми жидкостями.

Жидкообразные структурированные системы называются неньтоновыми жидкостями – их течение не подчиняется закону Ньютона, а вязкость зависит от напряжения сдвига. При некотором напряжении сдвига, называемом предельным, происходит полное разрушение структуры и система течет подобно ньютоновой жидкости, при этом вязкость системы становится минимальной.

Твердообразные структурированные системы характеризуются наличием первого (статического) предельного напряжения сдвига, до достижения которого жидкость не течет и не проявляет свойства ползучести. Для многих твердообразных тел разрушение структуры про­исходит при напряжениях, меньших предела текучести.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Какие структурированные системы называются коагуляционными? За счет каких сил они образуются?

2.В чем состоят особенности конденсационно–кристаллизационных структур?

3.Какие свойства называются тиксотропией и синерезисом?

4.Какие свойства относятся к структурно–механическим? Почему они так называются?

5.Какие зависимости изучает реология?

6.Какие жидкости называются ньютоновыми? Каким законам они подчиняются?

7.Какие участки имеются на кривых течения жидкообразных систем?

8.Какое явление называется ползучестью? Для какихсистем это явление наблюдается?

9.В чем состоят особенности течения твердообразных систем?

10, Что можно сказать о влиянии скорости сдвига на ньютоновскую вязкость для разных систем?

Закончив изучение главы 11, вы должны знать:

• причины структурообразования в дисперсных системах;

• виды структурированных дисперсных систем, их особенности;

• основные структурно–механические свойства разных систем.

ЧАСТЬ ТРЕТЬЯ

ЛИОФИЛЬНЫЕ СИСТЕМЫ

Большинство дисперсных системявляются лиофобными. Для них характерны:

• гетерогенность, наличие четко выраженной межфаз­ной границы;

• высокаястепень раздробленности дисперсной фазы;

• процесс диспергирования является несамопроизволь­ным, требует затраты энергии;

• наличие избытка свободной поверхностной энергии, что обусловливает стремлениек коагуляции. Свойства лиофобных систем былиподробно рассмот–рены в предыдущихглавах.

Теперь мы переходим к рассмотрению лиофильных систем, свойства которых принципиально отличаются от свойств лиофобных систем, а именно:

• образование этих систем происходит самопроизволь­но, часто с выделением энергии;

• имеет место сильное межмолекулярное взаимодействие между частицами дисперсной фазы и дисперсионной средой. Межфазовое поверхностное натяжение очень мало, а межфазовая граница размыта;

• системы являются термодинамически устойчивыми, что означает постоянство во времени концентрации и размеров частиц.

К лиофильным системам относятся:

• коллоидные поверхностно–активные вещества (ПАВ);

• растворы высокомолекулярных соединений (ВМС).

ГЛАВА 12

КОЛЛОИДНЫЕ ПОВЕРХНОСТНО–АКТИВНЫЕ ВЕЩЕСТВА

О поверхностно–активных веществах шла речь в свя­зи с адсорбцией молекул на поверхности жидкого раство­ра (глава 3). Вспомним определение ПАВ:

ПАВ – это вещества, добавление которых в гетеро­генную систему уменьшает поверхностное натяжение на границе раздела фаз. При этом во всем интервале концентраций вплоть до насыщенного раствора ПАВ находятся в молекулярно-дисперсном состоянии, т. е. системы являются гомогенными.

При удлинении углеводородной цепи до 8–10 атомов углерода возникает новое свойство – способность моле­кул ПАВ объединяться в агрегаты, содержащие десятки молекул и называемые мицеллами. При малых концент–рациях эти ПАВ образуют истинные растворы. При уве­личении концентрации раствора до определенной вели­чины, называемой критической концентрацией мицел-лообразования (ККМ), в растворе наряду с молекулами ПАВ присутствуют мицеллы, т. е. появляется новая фаза. Такие системы характеризуются двумя свойствами: вы­сокой дисперсностью и гетерогенностью, т. е. обладают свойствами коллоидных растворов.

Коллоидные ПАВ – это вещества, которые не толь­ко снижают поверхностное натяжение на границе раз­дела фаз, но при определенных концентрациях способны к самопроизвольному мицеллообразованию, т. е, к обра–зованию новой фазы.

Отличие коллоидных ПАВ от обычных заключается только в длине углеводородного радикала.