Энтальпии образования и сгорания

Изменение энтальпии, отвечающее образованию одного моля вещества из простых веществ взятых в той модификации и в том агрегатном состоянии, которые отвечают наиболее их устойчивому состоянию при данной температуре и стандартном давлении называют теплотой (энтальпией) образования. Теплоты образования принято обозначать _ΔfН⁰_(т), где индекс f (от английского - formation) означает, что речь идет о теплоте образования.

Для удобства сопоставления теплоты образования относят к температуре 298,15 К (25⁰С). Стандартные теплоты (энтальпии) образования _ΔfН⁰₂₉₈ можно найти в справочных таблицах термодинамических величин. Они измеряются в кДж/моль. Теплоты образования простых веществ в термодинамически устойчивом состоянии (Cl₂, H₂, O₂, S – ромбическая) при стандартных условиях принимаются равными нулю.

Стандартной энтальпией сгорания вещества (_ΔсН⁰₂₉₈) (от англ. сobustion - горение) называется изменение энтальпии _ΔrН⁰₂₉₈ в реакции окисления одного моля вещества кислородом с образованием соответствующих высших оксидов в стандартных условиях. Обычно эта величина применяется по отношению к органическим соединениям, поскольку многие из неорганических веществ негорючие. Для углеводородов продуктами сгорания являются СО_2(г), Н₂О_(ж). Азот, входящий в состав сжигающего соединения, переходит в N_2(г), галогены - Cl, Br, I, - в HCl_(г),, HBr_(г), HI_(г), сера – в SO_2(г). Стандартные энтальпии сгорания определены для многих веществ и приведены в справочнике физико-химических величин.

Закон Гесса и следствия из него

В 1840 году Г.И. Гесс экспериментально установил основной закон термохимии, который является частным случаем первого закона термодинамики применительно к химическим реакциям, протекающим в изохорных или изобатных условиях.

Закон Гесса устанавливает: если из данных исходных веществ можно получить заданные конечные вещества различными путями, то суммарная теплота на одном каком-нибудь пути равна суммарной теплоте процесса на любом другом пути, т.е. тепловой эффект химических реакций зависит только от начального вида и состояния исходных веществ и продуктов реакции, но не зависит от пути процесса (от способа перехода от исходного состояния к конечному).

Он подтверждает, что при V_,T = const,

Qv = _ΔrU⁰₂₉₈, а при Р_,Т = const,

Qр = _ΔrН⁰₂₉₈

Проиллюстрируем закон простой схемой

Процесс окисления аммиака до оксида азота может быть осуществлен в одну стадию:

4NH_3(г) + 5O_2(г) = 4NO_(г) + 6H₂O_(ж); _ΔrН⁰₂₉₈ = _ΔrН₁ = - 1166 кДж

Эту реакцию можно провести в две стадии: окислить аммиак кислородом с образованием газообразного азота и жидкой воды, а затем азот окислить до монооксида азота:

4NH_3(г) + 3O_2(г) = 2N_2(г) + 6H₂O_(ж); _ΔrН⁰₂₉₈ = _ΔrН₂ = - 1531,2 кДж

2N_2(г) + 2O_2(г) = 4NO_(г) ; _ΔrН⁰₂₉₈ = _ΔrН₃ = 365,2 кДж

_ΔrН₁ = _ΔrН₂ + _ΔrН₃

-1166 = -1531,2 + 365,2 кДж

Большое практическое значение для расчета тепловых эффектов реакций имеют следствия из закона Гесса.

Первое следствие. Тепловой эффект реакции равен разности между суммой теплот образования продуктов реакции и суммой теплот образования исходных веществ с учетом стехиометрических коэффициентов.

В качестве примера рассмотрим уравнение реакции записанной в общем виде:

v₁ А₁ + v₂ А₂ = v₃ А₃ + v₄ А_{4; Δr}Н⁰₂₉₈

_ΔrН⁰₂₉₈ = [v_{3 Δ}fН⁰₂₉₈ (А₃) + v_{4 Δ}fН⁰₂₉₈ (А₄) ] - [v_{1 Δ}fН⁰₂₉₈ (А₁) + v_{2 Δ}fН⁰₂₉₈ (А₂)]

Второе следствие. Тепловой эффект реакции равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания продуктов реакции с учетом стехиометрических коэффициентов.

Таким образом, для реакции:

v₁ А + v₂ В = v₃ С + v₄ D_{; Δr}Н⁰₂₉₈

_ΔrН⁰₂₉₈ = [v_{1 Δ}сН⁰₂₉₈ (А) + v_{2 Δ}сН⁰₂₉₈ (В) ] - [v_{3 Δ}сН⁰₂₉₈ (С) + v_{4 Δ}сН⁰₂₉₈ (D)]

Зависимость теплового эффекта от температуры.

Уравнение Кирхгофа.

Согласно закону Гесса можно вычислить тепловой эффект реакции при той температуре (обычно 298 К), при которой известны теплоты образования или сгорания всех реагентов. Часто бывает необходимо знать тепловой эффект реакции при различных температурах.

Запишем термодинамическое уравнение в виде:

v₁ А₁ + v₂ А₂ = v₃ А₃ + v₄ А_{4; Δr}Н⁰_(т)

Обозначив энтальпию образования i –того компонента, отнесенную к 1 молю через Н_i, энтальпию реакции представим в виде

_ΔrН⁰_(т) = (v₃ Н₃ + v₄ Н₄ ) - (v₁ Н₁ + v₂ Н₂ )

Продифференцируем данное уравнение по температуре при постоянном давлении:

(1.37)

Как следует из уравнения (1.30), производная является истинной теплоемкостью i – того реагента. Из уравнения (1.37) получим

[_ΔrН⁰_(т)] 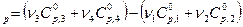(1.38)

или

[_ΔrН⁰_(т)] = _ΔС_р⁰ (1.38а)

Частную производную от теплового эффекта по температуре можно заменить на полную:

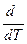(_ΔrН⁰_(т))_р = _ΔС_р⁰ (1.39)

Или

d(_ΔrН⁰_(т)) = _ΔС_р⁰ · dТ (1.40)

Выражения (1.39) и (1.40) называют уравнениями Кирхгофа в дифференциальном виде.Для практического применения интегрируют (1.40), используют неопределенный интеграл

_ΔrН⁰_(т) = _ΔН_{I +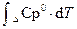} (1.41)

Где _ΔН_I - постоянная интегрирования или интегрируют в пределах от Т₁ до Т₂.

В качестве нижнего предела интегрирования обычно выбирают Т₁ = 298 К, так как _ΔrН⁰₂₉₈ легко вычислить по следствиям из закона Гесса

_ΔrН⁰_{(т )} = _ΔrН⁰₂₉₈ + 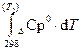(1.42)

В практике используют обе интегральные формулы. Формулы Кирхгоффа применяют в трех приближениях. В первом наиболее грубом полагают _ΔС_р = 0, т.е. считают равными суммарные теплоемкости продуктов и исходных веществ.

Тогда _ΔrН⁰_{(т )} = _ΔrН⁰_{(т )} = const, т.е. тепловой эффект считают независящим от температуры. Во втором, более точном приближении считают разность теплоемкостей постоянной величиной _ΔС_р⁰ = const; тогда _ΔС_р⁰ можно вывести за знак интеграла и для уравнения (1.42) получим следующую формулу второго приближения.

_ΔrН⁰_{(т )} = _ΔrН⁰₂₉₈ + _ΔС_р (Т₂ - 298)

В третьем, наиболее точном, приближении использования формулы Кирхгоффа учитывают зависимость _ΔС_р от температуры в виде степенного ряда С_р⁰ = а + вТ. Зависимость _ΔС_р⁰ = f(T) в общем виде записывается следующим образом: _ΔС_р⁰ = _Δа + _ΔвТ, где _Δа = Σv_ia_i (продуктов реакции) - Σv_ja_j (исходных веществ)

Аналогично для _Δв. При использовании формулы (1.42) при расчете в третьем приближении получим:

_ΔrН⁰_{(т )} = _ΔrН⁰₂₉₈ +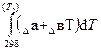

После интегрирования будем иметь:

_ΔrН⁰_{(т )} = _ΔrН⁰₂₉₈ + _Δа (Т₂ - 298) + 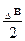(Т₂² – 298²)

Рассмотрим примеры решения задач, основанных на первом и втором следствиях из закона Гесса.

Пример № 1.

Рассчитайте стандартную энтальпию (стандартный )тепловой эффект при постоянном давлении реакции

СН_4(г) + 2О_2(г) → СО_2(г) + 2Н₂О_(ж)

Используя стандартные энтальпии образования исходных веществ и продуктов реакции.

Решение: По первому следствию из закона Гесса.

_ΔгН⁰₂₉₈ = _- =

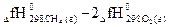= -393,5 + 2(- 285,8) - (-74,9) - 0 = -890,2 кДж < 0

Пример № 2.

По термохимическому уравнению рассчитайте стандартную энтальпию образования исходного вещества

2КС1О_3(кр) → КС1_(кр) + 3О_2(г); _ΔгН⁰₂₉₈ = -75,4 кДж.

Решение: По первому следствию из закона Гесса.

_ΔгН⁰₂₉₈ = 2 ,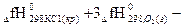

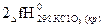Следовательно,

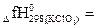0,5 (2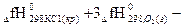 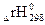,) = 0,5 [(2(-436,7) + 0 – (-75,4)] =

= 0,5 (-873,4 + 75,4) = -399 кДж/моль

Пример № 3.

Для реакции 2NO_(г) + О2_(г) → 2NO_2(г) рассчитайте стандартные тепловые эффекты при постоянном давлении (Q_р = _ΔгН⁰₂₉₈) и объеме (Q_v = _ΔгU⁰₂₉₈)

Решение:

Стандартный тепловой эффект при постоянном давлении найдем по первому следствию из закона Гесса

Q_р = _ΔгН⁰₂₉₈ = – 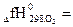2 * 34,2 – 2 * 91,3 - 0 = -114,2 кДж =

= - 114200Дм

По уравнению _ΔгН⁰₂₉₈ = _ΔгU⁰₂₉₈ + _ΔV_гRT

Q_v = _ΔгU⁰₂₉₈ = _ΔгН⁰₂₉₈ - _ΔV_гRT

Для данной реакции _ΔV_г = 2 – (2+1) = - 1 моль

Стандартный тепловой эффект при постоянном объеме

Q_v = _ΔгU⁰₂₉₈ = - 114200 – (-1) * 8,31 * 298 = - 111724 Дж = - 111,7 кДж

Пример № 4.

Стандартные энтальпии сгорания ацетилена С₂Н_2(г) и бензола С₆Н_6(г) соответственно равны – 1300 и – 3302 кДж /моль. Рассчитайте стандартную энтальпию реакции циклизации ацетилена.

3С₂Н_2(г) → С₆Н_6(г)

Решение: По второму следствию из закона Гесса

_ΔгН⁰₂₉₈ = = 3 (- 1300) – (- 3302) = - 598 кДж