Квантовомеханическая модель строения атома водорода. Квантовые числа электрона, форма s-,p- и d- орбиталей.
В 1924 г. французский физик Луи де Бройль высказал идею о том, что материя обладает как волновыми, так и корпускулярными свойствами. Согласно уравнению де Бройля (одному из основных уравнений квантовой механики),
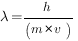
т. е. частице с массой m, движущейся со скоростью v соответствует волна длиной λ; h — постоянная Планка.
Длину волны такой частицы называют длиной волны де Бройля. Для любой частицы с массой т и известной скоростью v длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в 1927 г., когда были обнаружены у электронов как волновые, так и корпускулярные свойства. В 1927 г. немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую рх импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:
ΔxΔpx ≥ h;
ΔxΔpy ≥ h;
ΔxΔpz ≥ h.
Отсюда следует, что при точном определении координаты х микрочастицы исчезает информация о ее импульсе Δpx, так как при х=0 величина Δpx→∞. Если удастся снизить погрешность Δp,то будет велика погрешность Δх. Источник этих погрешностей заключен не в приборах, а в самой природе вещей.
Поскольку постоянная Планка очень мала, то ограничения, накладываемые принципом неопределенности, существенны только в масштабах атомных размеров. Согласно принципу неопределенности, невозможно утверждать, что электрон, имеющий определенную скорость, находится в данной точке пространства, здесь можно использовать лишь вероятностное описание.
Для описания свойств электрона используют волновую функцию, которую обозначают буквой Ψ (пси). Квадрат ее модуля |Ψ|2, вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину |Ψ|2 называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями r и (r+dr) от ядра. Объем, лежащий между двумя сферами, имеющими радиусы r и (r+dr), равен 4Πr2dr, а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности |Ψ|2 достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение r для электрона атома водорода равно радиусу орбиты a0 соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого электронного облака
Чем больше величина |Ψ|2, тем больше вероятность нахождения электрона в данной области атомного пространства.
В квантовой механике вместо термина «орбита» используют термин «орбиталь», которым называют волновую функцию электрона. Соответственно орбиталь характеризует и энергию и форму пространственного распределения электронного облака. Расчеты в квантовой механике проводят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном-пространстве.
В простейшем случае уравнение Шредингера может быть записано в виде
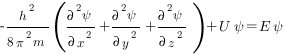
где h — постоянная Планка; m — масса частицы; U — потенциальная энергия; Е — полная энергия; х, у, z — координаты; Ψ — волновая функция.
Решая уравнение Шредингера, находят волновую функцию Ψ=f(x, y, z). Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию можно оценить величину |Ψ|2dV — вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро.
Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He+, Li2+ и т. д.). В этом случае энергия электрона
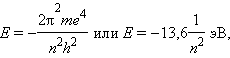
где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.
В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
Орбитальное квантовое число l характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых l имеет буквенные обозначения.
Электроны с одинаковым значением l образуют подуровень.
Квантовое число l определяет квантование орбитального момента количества движения электрона 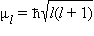 в сферически симметричном кулоновском
в сферически симметричном кулоновском
поле ядра.
Квантовое число ml называют магнитным. Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения Mz на какую-либо ось координат (обычно ось z):
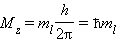
Граничные поверхности s-, p-, d-, f- орбиталей показаны на рис.
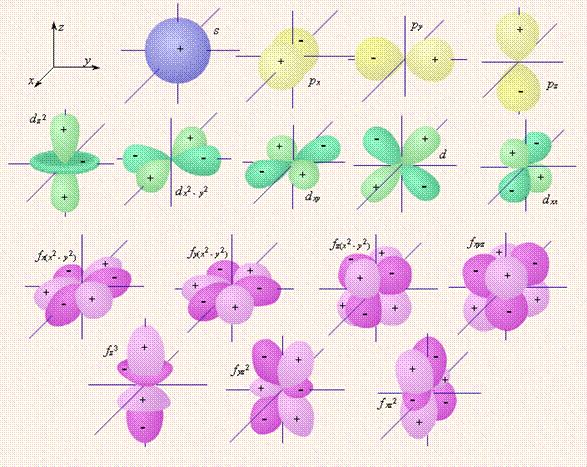
s-Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μl = 0.
p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz.
d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² и dx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz.
2.Равновесия в водных растворах солей, содержащих многозарядные катионы металлов. Вычисление pH (приведите примеры).
Аквакомплексы представляют собой ионы или молекулы, в которых лигандами служат молекулы воды. В водных растворах солей почти все ионы существуют в виде акваионов, например, [Be(H2O)4]2+, [Al(H2O)6]3+, [Cr(H2O)6]3+ и т.д. При кристаллизации таких солей из водных растворов вода остается связанной с комплексообразователем:
[Be(H2O)4]SO4, [K(H2O)6][Al(H2O)6](SO4)2, [Cr(H2O)6]Cl3.
К аквакомплексам относятся многие кристаллогидраты, например, [Al(H2O)6]Cl3 (иначе – AlCl3 . 6 H2O), [Cr(H2O)6](NO3)3 (иначе – Cr(NO3)3 . 6 H2O).
У некоторых кристаллогидратов часть молекул воды входит во внутреннюю, а остальные находятся во внешней сфере и связываются с внешнесферными ионами.
Например, пентагидрат сульфата меди(II) и гептагидрат сульфата никеля(II) содержат аквакомплексы – катион тетрааквамеди(II) и катион гексаакваникеля(II) и слабо связанную внешнесферную молекулу воды, которая объединяет катионы и анионы посредством водородных связей:
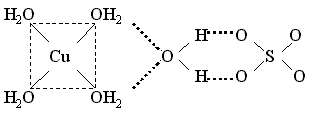
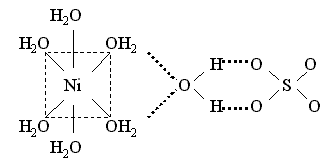
Координационные формулы указанных соединений, учитывающие состав внутренней и внешней сферы, таковы:
[Cu(H2O)4]SO4 . H2O и
[Ni(H2O)6]SO4 . H2O.
Все аквакатионы, за исключением тех, которые образованы щелочными и щелочноземельными элементами, а также таллием(I), серебром(I) и т.п., являются катионными кислотами, в водном растворе подвергаются протолизу и создают кислотную среду (рН < 7):
[Zn(H2O)4]2+ + H2O = [Zn(H2O)3(OH)]+ + H3O+
Кислотные свойства аквакомплексов выражены тем сильнее, чем выше степень окисления атома-комплексообразователя.
Например, значения констант кислотности для производных железа(II) и железа(III) составляют 1,8 . 10- 7 и 6,8 . 10-3. Следовательно, равновесие протолиза в случае аквакомплекса железа(III) в большей степени смещено вправо, чем для железа(II).
В качестве примера возьмем гидролиз ацетата натрия:
CH3COONa+HOH<—>CH3COOH+NaOH
Ионное уравнение:
CH3COO-+HOH<—>CH3COOH+OH-
Константа равновесия этой реакции
K=[CH3COOH]•[OH-]/[CH3COO- ]•[HOH]
так как концентрация воды практически остается постоянной, ее можно объединить с константой равновесия:
Kг=K•[H2O]=[CH3COOH]•[OH-]/[CH3COO-]
где Кг - константа гидролиза.
Выразим [OH-] через ионное произведение воды [OH-] =Kв / [H+] и
подставив эту величину в уравнение Кг получаем
Kг=K•Kв =[CH3COOH]•[OH-]/[CH3COO-]•[H+] =Kв/Kk
где Kk - константа диссоциации слабой кислоты.
В общем случае, если исходную концентрацию аниона слабой кислоты А- -обозначить через С моль/л, то Ch моль/л – это концентрация той части аниона А-, которая подверглась гидролизу и образовала Ch моль/л слабой кислоты HA и Ch моль/л гидроксильных ионов:A- + HOH <—> HA + OH-
C-Ch Ch Ch
где: h – степень гидролиза, т.е доля молекул соли, подвергающихся гидролизу.
Константа гидролиза соли: 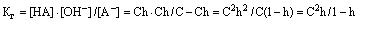
При малом значении h: Kг=Сh2 откуда 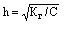 .
.
Так как [HA]=[OH-]=C , то Kг=[OH- ]2 /C; [H+]=Kв/[OH- ]=Kв/Kк , pH=-lg[H+].
Аналогично соотношение можно получить и при рассмотрении гидролиза соли слабого основания и сильной кислоты:
Kг=[OH- ]2 /C; [H+]=Kв/[OH- ]=Kв/Kосн
Пример: Определить pH 0.02Н раствора соды Na2C03, учитывая только первую ступень гидролиза.
Решение: Гидролиз соли протекает по уравнению
Na2CO3+HOH=NaOH+NaHCO3 или CO32-+HOH=OH-+HCO3 -
Kг=Kв/Kк=10-14/4,7•10-11=2,1•10-4
Для вычисления степени гидролиза необходимо вычислить молярную концентрацию раствора
С (Na2CO3)=0,01 моль/л
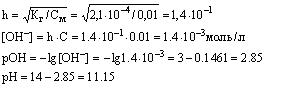
Уравнения реакций.
2KMnO4+10FeSO4+8H2SO4= 5Fe2(SO4)3 + K2SO4 + 2MnSO4 + 8H2O
Na3AsO4 + H2O =Na2HAsO4 + NaOH
