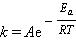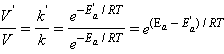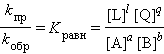Температура и скорость реакции.

При фиксированной температуре реакция возможна, если взаимодействующие молекулы обладают определённым запасом энергии. Аррениус эту избыточную энергию назвал энергией активации, а сами молекулы активированными.

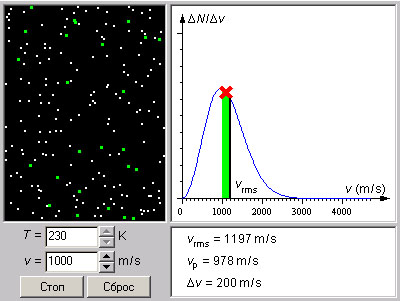Модель 5.2. Распределение Максвелла. Модель иллюстрирует тепловое движение молекул газа (молекулярный хаос). Предусмотрена возможность отмечать все молекулы, скорости которых попадают в некоторый выбранный интервал скоростей. На экране дисплея можно наблюдать кривые распределения молекул по скоростям для различных температур. Молекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры T. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а величины скоростей подчиняются определенной закономерности. Распределение молекул газа по величине скоростей называется распределением Максвелла. Если одновременно измерить скорости большого числа N молекул газа и выделить некоторый малый интервал скоростей от v до v + Δv, то в выделенный интервал Δv попадает некоторое число ΔN молекул. На графике удобно изображать зависимость величины (ΔN / Δv) от скорости v. При достаточно большом числе N эта зависимость изображается плавной кривой, имеющей максимум при v = vв = ((2kT) / m)1/2 (наиболее вероятная скорость). Здесь m – масса молекулы, k = 1,38·10–23 Дж/К – постоянная Больцмана. Характерным параметром распределения Максвелла является так называемая среднеквадратичная скоростьvкв = <v2>1/2, где <v2> означает среднее значение квадрата скорости, которая равна vкв = ((3kT)/m)1/2 = ((3RT)/μ)1/2, где μ – молярная масса. Из выражения для среднеквадратичной скорости следует, что средняя кинетическая энергия поступательного движения молекул газа есть <E> = (m<v2>) / 2 = 3/2kT На экран выводится кривая распределения при заданной температуре и вычисляются среднеквадратичная vкв и наиболее вероятная vв скорости. Можно изменять температуру газа T и наблюдать смещение максимума кривой распределения. Все молекулы, скорости которых попали в выделенный интервал, окрашиваются в зеленый цвет. Среднюю скорость молекул, попавших в выделенный интервал, можно изменять, перемещая интервал по оси скоростей. Можно качественно наблюдать за количеством и скоростью движения окрашенных молекул. Обратите внимание, что количество зеленых молекул максимально, когда выделенный интервал скоростей располагается вблизи максимума кривой распределения. Скорость таких молекул совпадает с наиболее вероятной скоростью vв.

По Аррениусу константа скорости k и энергия активации E_a связаны соотношением, получившим название уравнения Аррениуса:

(5.3)

Здесь A – предэкспоненциальный множитель, R – универсальная газовая постоянная, T – абсолютная температура.

Таким образом, при постоянной температуре скорость реакции определяет E_a. Чем больше E_a, тем меньше число активных молекул и тем медленнее протекает реакция. При уменьшении E_a скорость возрастает, а при E_a = 0 реакция протекает мгновенно.

Величина E_a характеризует природу реагирующих веществ и определяется экспериментально из зависимости k = f(T). Записав уравнение (5.3) в логарифмическом виде и решая его для констант при двух температурах, находим E_a:

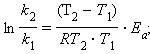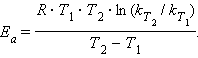Если E_a = 50–100 кДж∙моль^–1, то из уравнения Аррениуса следует, что при изменении температуры реакции на 10 градусов ее скорость изменится в 2–4 раза. Это правило было эмпирически установленно Вант-Гоффом:

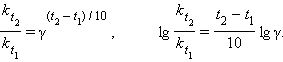γ – температурный коэффициент скорости химической реакции. Правило Вант-Гоффа имеет ограниченное применение, поскольку величина γ зависит от температуры, а вне области E_a = 50–100 кДж ∙ моль^–1 это правило вообще не выполняется.

На рис. 5.4 видно, что затрачиваемая на перевод начальных продуктов в активное состояние (А* – активированный комплекс) энергия затем полностью или частично вновь выделяется при переходе к конечным продуктам. Разность энергий начальных и конечных продуктов определяет ΔH реакции, которая от энергии активации не зависит.

Таким образом, по пути из исходного состояния в конечное система должна преодолеть энергетический барьер. Только активные молекулы, обладающие в момент столкновения необходимым избытком энергии, равным E_a, могут преодолеть этот барьер и вступить в химическое взаимодействие. С ростом температуры увеличивается доля активных молекул в реакционнной среде.

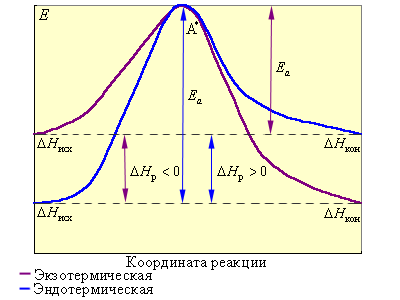Рисунок 5.4. Реакционный путь экзотермической и эндотермической реакции A + B → D; A* – переходное состояние, активированный комплекс.

Предэкспоненциальный множитель A характеризует общее число соударений. Для реакций с простыми молекулами A близок к теоретической величине столкновений Z, т. е. A = Z, рассчитываемой из кинетической теории газов. Для сложных молекул A ≠ Z, поэтому необходимо вводить стерический фактор P:

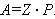Стерический фактор учитывает то обстоятельство, что для взаимодействия сложных активных молекул необходима определенная взаимная ориентация: течению процессов способствует столкновение молекул в положениях, когда в соприкосновение приходят их реакционноспособные связи или неподеленные пары электронов.

Таким образом, уравнение Аррениуса имеет вид

Здесь Z – число всех соударений, P – доля соударений, благоприятных в пространственном отношении (принимает значения от 0 до 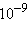), 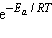– доля активных, т. е. благоприятных в энергетическом отношении соударений.

Размерность константы скорости получается из соотношения

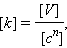и, как видно из уравнения Аррениуса, размерность предэкспоненты та же.

Для T = 300 K и концентраций, выраженных в моль∙л^–1, Z имеет следующие приблизительные значения в реакциях различной молекулярности:

n = 1	n = 2	n = 3
1013–1014 c–1	1011–1012 л∙моль–1c–1	109–1011 л∙моль–1c–1

Анализируя выражение (5.3), приходим к выводу, что существуют две принципиальные возможности ускорения реакции:
а) увеличение температуры,
б) снижение энергии активации.

Катализ.

Изменить величину E_a можно с помощью катализаторов. Вещества, принимающие участие, но не расходующиеся в процессе реакции, назваются катализаторами. Само это явление называется катализом.

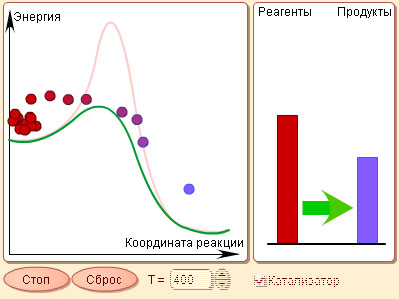Модель 5.3. Катализ.   С помощью этой модели вы можете познакомиться с энергетической подоплекой процесса катализа. На графике изображена условная кривая зависимости энергии реагентов от хода реакции. Потенциальный барьер не позволяет протекать реакции при низких температурах (когда энергия теплового движения недостаточна для преодоления этого барьера). С помощью поля ввода с кнопками прокрутки, расположенного в нижней части модели, вы можете изменять температуру. Вы сможете убедиться, что только при самых высоких температурах модельная реакция может протекать без катализатора. В присутствии же катализатора энергетический барьер значительно снижается или пропадает вовсе, значительно увеличивая скорость реакции. В окне, расположенном справа от окна реакции, располагается столбиковая диаграмма, которая показывает количество исходных компонентов и прореагировавшего к данному моменту вещества.

В зависимости от того, находится ли катализатор в той же фазе, что и реагирующие вещества, или образует самостоятельную фазу, говорят о гомогенном или гетерогенном катализе. Механизм каталитического действия для них не одинков, однако и в том и в другом случае происходит ускорение реакции за счет снижения E_a.

Так, медленно протекающая реакция A + B → А…B → AB (ΔG < 0) в присутствии катализатора идет с большей скоростью в две стадии:

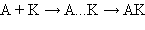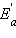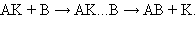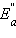т. е. образуются частицы промежуточного соединения AK (катализатора с реагентами), затем активный комплекс AKB и конечные продукты с регенерацией катализатора. Следовательно, каталитический путь оказывается кинетически более выгодным, чем прямое взаимодействие исходных веществ. Существует ряд специфических катализаторов – ингибиторов, снижающих скорость реакции.

Рисунок 5.5. Изображение реакционного пути некаталитической A + B → AB реакции (кривая 1) и гомогенной каталитической реакции (кривая 2).

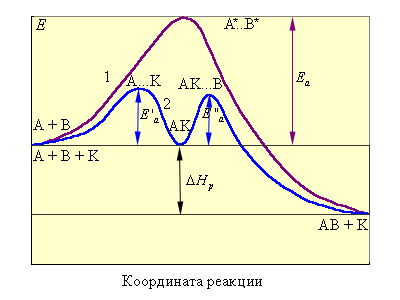
Увеличение скорости реакции в присутствии катализатора определяется формулой

где – параметры каталитического процесса, V, k, 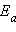– некаталитического процесса ln /k = 2,303 lg /k = ( 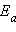– 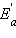) / RT.

Сложные реакции.

Большинство химических реакций идут не в одну стадию, но и одностадийная реакция может кинетически осложняться, если она обратима. К кинетически сложным реакциям относят также последовательные, параллельные, цепные, фотохимические и некоторые другие.

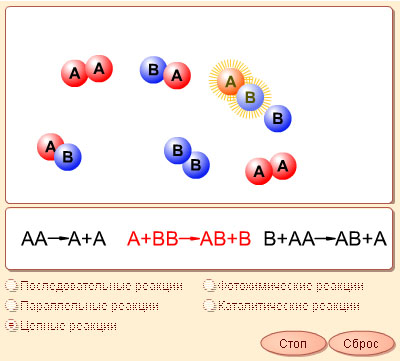Модель 5.4. Типы реакций.   Эта модель демонстрирует различные типы химических реакций. В главном окне модели вы увидите сами реакции, а в окне, находящемся под ним, – уравнения происходящих процессов (подсвечивается то из них, которое описывает реакцию, идущую в данный момент). В последовательные реакции, то увидите, как происходит несколько условных реакций, причем продукты первой входят в число исходных веществ второй реакции и т. д. В параллельных реакций, вы сможете увидеть, как одно и тоже вещество реагирует параллельно с различными ингредиентами (давая в результате различные продукты). В случае цепных реакций молекула одного из исходных веществ в результате поглощения кванта энергии распадается на два радикала, которые затем атакуют молекулы другого вещества. Те отдают по одному атому для образования смешанной молекулы, другой же атом распавшейся молекулы остается и точно так же играет роль радикала. Реакция продолжается далее по цепочке. В фотохимических реакциях молекулы одного из исходных веществ должны поглотить по кванту света, после чего переходят в возбужденное состояние. В этом состоянии они способны вступать в реакцию со вторым исходным веществом или диссоциировать. Наконец, рассмотрите процесс протекания каталитических реакций. При отсутствии катализатора они протекают крайне вяло или же не идут вовсе. Наличие катализатора радикально изменяет ситуацию. Молекулы одного из исходных веществ охотно соединяются с катализатором, а затем с этим комплексом взаимодействуют молекулы второго исходного вещества. Образуется конечный продукт, а катализатор отщепляется и снова готов участвовать в реакции.

Обратимые реакции.

Особенность обратимых реакций состоит в том, что по мере накопления продуктов реакции возрастает скорость обратной реакции. Если они сравняются, то наступает равновесное состояние. Для реакции

ЗДМ для прямой реакции V_пр = k_пр [A]^a [B]^b, для обратной реакции V_обр = k_обр [L]^l [Q]^q. При условии V_обр = V_пр получаем

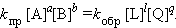При отношении 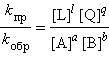получаем выражение ЗДМ для обратимой реакции

Для одностадийной реакции

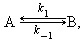где k₁ – константа скорости прямой реакции, k_–1 – константа скорости обратной реакции.

При наступлении равновесия k₁ [A] = k_–1 [B], следовательно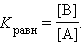

Предположим, что А может превратиться в B через промежуточную стадию образования C:

Возможен ли такой циклический процесс? Оказывается, такой циклический процесс запрещен в силу принципа детального равновесия (микроскопической обратимости), согласно которому для равновесного химического процесса всякая элементарная реакция должна идти со скоростью, в точности равной скорости реакции. То есть, в обратимой элементарной реакции прямая и обратная реакции протекают через одно и то же переходное состояние. Справедлива схема

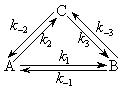
Эти шесть констант скорости не являются независимыми, поскольку k_–1 k₂ k₃ = k₁ k_–2 k_–3.