Развитие и становление биофизики как науки

Предмет и задачи биофизики

Предметом биофизики является изучение физических и физико-химических процессов, лежащих в основе жизни. По природе объектов исследования, биофизика является типичной биологической наукой, а по методам изучения и анализа результатов исследования является своеобразным разделом физики. Биофизические методы созданы на основе физических и физико-химических методов изучения природы. В этих методах должны сочетаться трудно совместимые качества: 1. Высокая чувствительность. 2. Большая точность. Этим требованиям не удовлетворяют полностью никакие методы, однако, наиболее широкое применение получили для биофизических исследований следующие методы: - оптические; - радио спектроскопия - ультразвуковая радиоскопия; - электронно-парамагнитная резонансная спектроскопия (ЭПР); - ядерная магнитная резонансная спектроскопия. Необходимо отметить, что любые исследования требуют, чтобы регистрирующие приборы не вносили искажений в изучаемый процесс, однако, трудно сравнить какую-либо физическую систему с живым организмом по необычайно высокой чувствительности организма к любым воздействиям на него. Воздействия не просто нарушают нормальный ход биологических процессов, а вызывают сложные приспособительные реакции, разнообразные в различных органах и в различных условиях. Искажение смысла измерений может оказаться столь существенным, что становится невозможно вносить поправки в явления, не свойственные изучаемому объекту. При этом, методы коррекции, используемые с успехом в физике и технике, зачастую бесполезны в биофизике. Для лучшего понимания области применения биофизических методов, рассмотрим основные направления исследований в биофизике: 1) молекулярная и квантовая биофизика изучают физическую структуру и свойства биологически важных молекул, физические процессы, которые обеспечивают их функционирования, а также исследуют термодинамику биологических систем, перенос энергии и заряда по биомолекулам, квантово-механические особенности их строения; 2) биофизика клетки связана с физическими и физико-химическими свойствами клеточных и субклеточных структур, закономерностями их деления, с особенностями их обмена веществ (метаболизмом), а также, с биофизическими механизмами специальных функций клеток; 3) биофизика органов чувств скрывает физические и физико-химические механизмы восприятия раздражителя рецепторами аппарата сенсорных систем человека и животных на квантовом, молекулярном или клеточном уровнях; 4) биофизика сложных систем изучает проблемы межклеточного взаимодействия, передачи информации в биологических каналах связи и управления функциями живых организмов; 5) биофизика внешних воздействий изучает механизмы воздействия на организм физических факторов среды (например, полей)

Понятие математической модели. Задачи и возможности математического моделирования в биологии. Понятие адекватности модели реальному объекту. Принципы построения математических моделей биологических систем.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ - представление изучаемого в конкретно-научном знании явления или процесса на языке математических понятий. При этом ряд свойств исследуемого явления предполагается получить на пути исследования собственно математических характеристик модели. Построение М.м. чаще всего диктуется необходимостью иметь количественный анализ изучаемых явлений и процессов, без которого, в свою очередь, невозможно делать проверяемые на опыте предсказания об их протекании.

М а т е м а т и ч е с к и е модели строятся на основе данных эксперимента или умозрительно, формализованно описывают гипотезу, теорию или открытую закономерность того или иного биологического феномена и требуют дальнейшей опытной проверки. Различные варианты подобных экспериментов выявляют границы применения математических моделей и дают материал для ее дальнейшей корректировки. «Проигрывание» математической модели биологического явления на ЭВМ позволяет предвидеть характер изменения исследуемого биологического процесса в условиях, трудно воспроизводимых в эксперименте. Математические модели позволяют в отдельных случаях предсказать некоторые явления, ранее неизвестные исследователю. Так, модель сердечной деятельности, предложенная голландскими учеными ван дер Полом и ван дер Марком, основанная на теории релаксационных колебаний, указала на возможность особого нарушения сердечного ритма, впоследствии обнаруженного у человека. Это позволяет изучать в эксперименте механизмы возникновения данного состояния или заболевания, его течение и исход, воздействовать на его протекание.

Адекватность модели – это степень ее соответствия реальному объекту. Критерием адекватности модели служит только практика, только эксперимент на реальном объекте.

Адекватность предполагает воспроизведение моделью с необходимой полнотой всех характеристик объекта, существенных для цели моделирования.

Так как всякую модель можно сравнить с проекцией, нельзя говорить об абсолютной адекватности, при которой модель по всем параметрам соответствует оригиналу, тем более когда строятся модели природных или социальных явлений и процессов (неконструктивных объектов).

Принципы построения математических моделей

1. Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель.

2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время.

3. Принцип множественности моделей. Данный принцип является ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс.

4. Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования.

5. Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели. Степень реализации перечисленных принципов и каждой конкретной модели может быть различной, причем это зависит не только от желания разработчика, но и от соблюдения им технологии моделирования. А любая технология предполагает наличие определенной последовательности действий

5. Методы качественной теории дифференциальных уравнений в анализе динамических свойств биологических процессов. Понятие фазовой плоскостиПростейшие модели этих двух систем впервые были предложены независимо А. Д. Лоткой в 1926 г. модель химической реакции и В. Вольтерра в 1931 г. модель хищник - жертва. Пусть имеется химическая реакция, протекающая по общей схеме А Х Y В- Молекулы А с некоторой постоянной скоростью ко превращаются в молекулы вещества X реакция нулевого порядка. Вещество X может превращаться в вещество Y. Важная особенность состоит в том, что скорость этой реакции тем больше, чем больше концентрация вещества Y. Это означает, что превращение X зависит не только от концентрации исходного реагента X, но и от продукта превращения Y. Иными словами, скорость этой реакции зависит от концентрации обоих веществ - исходного X и конечного У , а сама реакция протекает как реакция второго порядка.

Такие процессы, где скорость превращения исходного вещества пропорциональна концентрации продукта реакции, носят название автокаталитических.

Молекулы Y, в свою очередь, необратимо распадаются, в результате образуется вещество В. Ээкологическая модель Вольтерра. Пусть в некотором замкнутом районе живут жертвы и хищники, например зайцы и волки. Зайцы питаются растительной пищей, всегда имеющейся в достаточном количестве. Волки хищники могут питаться лишь зайцами жертвами. Обозначим число зайцев х, а число волков - у. Так как количество пищи для зайцев не ограничено, мы можем предположить, что зайцы размножаются со скоростью, пропорциональной их числу.

Пусть убыль численности зайцев пропорциональна вероятности встречи их с волками, т.е. пропорциональна произведению х х у. Количество волков также нарастает тем быстрее, чем чаще их встречи с зайцами, т.е. пропорционально х х у. В химической кинетике это соответствует бимолекулярной реакции, когда вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, т. е. произведению их концентраций. Кроме того, имеет место естественная смертность волков, причем скорость убывания численности особей пропорциональна их количеству.

Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка.[1] Фазовая плоскость является частным случаем фазового пространства, которое может иметь бо́льшую размерность.

В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат — первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство).[2]

Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой.[3] Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных состояний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц.

6. Стационарные состояния биологических систем. Устойчивость стационарных состояний.

Состояние системы, при котором ее параметры не изменяются в течение длительного времени, но происходит обмен веществом и энергией с окружающей средой, называют стационарным. В стаци­онарном состоянии открытой системы концентрация промежуточ­ных продуктов не изменяется со временем. Живой организм в каждый момент времени не отвечает приве­денному определению стационарного состояния. Стационарное состояние характерно для организма. Так, с большим постоянством поддерживается температура определен­ных органов и тканей у теплокровных животных, сохраняется неиз­менный солевой состав и водородный показатель (рН) различных биологических жидкостей, не изменяются в ходе нормальной жиз­недеятельности величины биопотенциалов покоя, осмотического давления.

В открытых системах суммарное изменение энтропии в стацио­нарном состоянии равно нулю.

Стационарное состояние биологической системы поддерживается, когда увеличение энтропии системы за счет происходящих в ней необратимых процессов компенсируется оттоком энтропии при взаимодействии с окружающей средой.

характерными свойст­вами стационарного состояния являются стремление системы к ми­нимуму ежесекундного прироста энтропии и определенная внут­ренняя стабильность и упорядоченность.

В организме поддерживается гомеостаз в течение времени, про­текающего от рождения до смерти. Уровни стационарных состояний в течение онтогенеза постоянно изменяются. У детей уровень Са2+ в костях с их ростом увеличивается, изменяется количество зубов, волос и т. д. Это примеры перехода на новые стационарные уровни, примеры необратимых изменений.

Живой организм может изменить уровень стационарного состоя­ния в результате воздействия окружающей среды и при патологиче­ских процессах.

Одной из важнейших характеристик биологических систем явля­ется устойчивость стационарных состояний. Устойчивое стационар­ное состояние характеризуется тем, что при отклонении системы от стационарного уровня в ней возникают силы, стремящиеся вернуть ее в первоначальное положение. Пример – шарик в ямке (с трением или без трения).

Внешние воздействия вызывают в неустойчивой стационарной системе нарастающие изменения, в результате которых система пе­реходит или в устойчивое стационарное состояние (при дополни­тельной затрате энергии), или в состояние термодинамического равновесия. Пример: шарик на горке

Любое отклонение от уровня стационарности вызовет в системе увеличение скорости продуцирования энтропии.

Система, которая функционирует в одном из двух устойчивых стационарных состояний, характеризуется триггерными свойства­ми, обеспечивающими направленные и скачкообразные переключе­ния из одного стационарного состояния в другое. Например, при раздражении нервного волокна состояние возбуждения наступает скачкообразно после достижения порога возбуждения. Триггерные свойства биологиче­ских систем определяют и процесс клеточной дифференциации, когда при делении возникают дочерние клетки, качественно отлич­ные от клеток-предшественников.

7.Биологические системы включают большое число процессов с разными характерными временами, причем иерархия этих времен такова, что они различаются на много порядков. Примером такой иерархической системы является процесс фотосинтеза, который обеспечивает существование жизни на Земле. Процессы поглощения энергии квантов света молекулами хлорофилла имеют характерное время порядка 10^-12 с, процессы фотосинтетического электронного транспорта на разных его участках – 10^-9-10^-2 с, процессы фиксации углерода – секунды и минуты, процессы транспорта минеральных веществ – минуты и часы. Рост растений может продолжаться дни и годы. Математическая модель, описывающая процессы с разными характерными временами, может быть упрощена с учетом иерархии времен. Медленно изменяющиеся переменные можно считать «параметрами», если внимание исследователя сосредоточено на изучении переменных со «средними» характерными временами. Для «быстрых» переменных дифференциальные уравнения могут быть заменены алгебраическими. Таким образом предполагается, что «быстрые» переменные при изменении «медленных» практически мгновенно «подстраиваются», при этом устанавливаются квазистационарные концентрации быстрых переменных. Математические условия применения Метода стационарных концентраций сформулированы в теореме выдающегося русского математика А. Н. Тихонова. Система уравнений сводится к системе с малыми множителями при производной в правой части уравнений.

Пример применения теоремы Тихонова – вывод уравнения простейшей ферментативной реакции Михаэлиса-Ментен. Реакция описывает образование продукта из субстрата с участием фермента, общая концентрация которого остается постоянной. Предполагается, что общая концентрация субстрата значительно превосходит концентрацию фермента. Такое соотношение концентраций обеспечивает наличие малого множителя и означает, что скорость изменения концентрации фермента значительно превосходит скорость изменения концентрации субстрата.

Принцип узкого места (ПУМ) основан на разделении всех переменных, характеризующих свойства системы на быстрые и медленные. Характерное время процесса – t отражает время развития процесса. t процессов ферментативного катализа 10^–1 – 10^–6 с, процессы физиологической адаптации, для них t несколько минут и больше, процессы репродукции в этой же системе, для них t несколько минут и больше. t – величина противоположная скорости. V=1/t. В пределах одной отдельной цепочки взаимосвязанных реакций всегда имеются наиболее медленные и наиболее быстрые стадии.

Согласно ПУМ общая скорость всей цепи реакций определяется наиболее медленной стадией (она и есть узкое место), она имеет самое большое t, V_min. Общее время всей цепи реакций (всего процесса) будет мало отличаться от характерного времени узкого места. Чтобы воздействовать на время процесса нужно воздействовать на узкое место.

При внешних возмущениях в системе наблюдаются изменения как быстрых, так и медленных перменных, однако эти изменения протекают с разной скоростью. В устойчивой системе быстрые переменные быстро отклоняются от своих начальных значений, но быстро в них возвращаются. Медленные переменные изменяются в ходе длительных переходных процессов, определяющих динамику всей системы. Фактически быстрые переменные колеблются возле своих стационарных значений. Поэтому вместо диф уравнения, описывающего динамику быстрой переменной можно записать алгебраическое уравнение, отражающее ее стационарное значение, что приведет к постоянному уменьшению числа диф уравнений в системе, останутся лишь те, что описывают наиболее медленные процессы.

dx/dt=AF(x;y)

dy/dt=Q(x;y)

A>>1 Þ A*F>> 1 Þ x быстрая переменная (dx/dt быстрая величина, скорость D х велика)

делить на А

e(dx/dt)=F(x;y), где e=1/A, e<<1, e®0, F(x;y)=0, e=0

Следовательно у является управляющим параметром, влияющим на координаты в стационарной точке. В био системах роль узкого места могут выполнять разные звенья цепи в зависимости от условий.

Изменение энтропии в открытых системах. Термодинамические условия осуществления стационарного состояния. Связь межу величинами химического сродства и скоростями реакций. Термодинамическое сопряжение реакций и тепловые эффекты в биологических системах.

Применение второго закона к биологическим системам в его классической формулировке приводит, как кажется на первый взгляд, к парадоксальному выводу, что процессы жизнедеятельности идут с нарушением принципов термодинамики. В самом деле, усложнение и увеличение упорядоченности организмов в период их роста сопровождаются кажущимся уменьшением, а не увеличением энтропии, как должно было бы следовать из второго закона. Однако увеличение энтропии в необратимых самопроизвольных процессах происходит в изолированных системах, а биологические системы являются открытыми. Проблема поэтому заключается в том, чтобы, во-первых, понять, как связано изменение энтропии с параметрами процессов в открытой системе, а во-вторых, выяснить, можно ли предсказать общее направление необратимых процессов в открытой системе по изменению ее энтропии. Главная трудность в решении этой проблемы состоит в том, что мы должны учитывать изменение всех термодинамических величин во времени непосредственно в ходе процессов в открытой системе.

Итак, необходимо рассматривать организм не изолированно от внешней среды, а во взаимодействии с ней. Как известно, в изолированной системе самопроизвольно протекающие процессы приводят ее к состоянию так называемого термодинамического равновесия. При этом состоянии градиенты энергии выровнены, работоспособность системы равна нулю, а ее энтропия максимальна. Однако хорошо известно, что биологические системы, пока они функционируют, никогда не достигают такого состояния. Они всегда обладают работоспособностью, а их энтропия не максимальна. Это связано с тем, что биосистемы являются не изолированными, а открытыми системами. Они постоянно обмениваются энергией с внешней средой. При этом свободная энергия поступает в организм в виде пищевых продуктов, различных излучений и т.д, а выделяется чаще всего в деградированной тепловой форме или в виде низкоэнергетических соединений. Поскольку приток свободной энергии способствует уменьшению энтропии системы (увеличиваются градиенты энергии, уменьшается количество деградированной формы энергии), то нередко говорят, что организм питается отрицательной энтропией и выделяет положительную энтропию. Исходя из сказанного, для рассмотрения приложимости второго принципа термодинамики к биосистемам следует брать не организм как таковой, а организм вместе с участком среды, обеспечивающим его нормальное функционирование в течение определенного времени. Такая система получила название условно изолированной системы. В ней второй принцип термодинамики полностью приложим. В отдельных участках этой системы энтропия, казалось бы вопреки второму принципу термодинамики, может даже уменьшаться (например, в зеленом листе при фотосинтезе). Однако это уменьшение происходит за счет возрастания энтропии в другой части такой системы (например, в источнике света, от которого световая энергия поступает в лист). В результате общая энтропия такой системы в соответствии со вторым принципом термодинамики не уменьшается, а имеет тенденцию к увеличению. Таким образом, можно констатировать, что, так же как и к неживым объектам, второй принцип термодинамики приложим и к биосистемам. Протекание процессов в них идет в соответствии с этим принципом и энтропии здесь принадлежит важная роль.
Таким образом, постулат И.П. Пригожина состоит в том, что общее изменение энтропии dS открытой системы может происходить независимо либо за счет процессов обмена с внешней средой (d_eS), либо вследствие внутренних необратимых процессов (d_iS): dS=d_eS+d_iS.
Во всех реальных случаях d_iS>0, и только если внутренние процессы идут обратимо и равновесно, то d_iS=0. Для изолированных систем d_eS= 0, и это классическая формулировка второго закона: dS = d_iS =0. В клеточном метаболизме всегда можно выделить такие две группы процессов. Например, поступление извне глюкозы, выделение наружу продуктов ее окисления (d_eS) и окисление глюкозы в процессах дыхания (d_iS). В фотосинтезе приток свободной энергии света приводит к уменьшению энтропии клетки d_eS<0, а процессы дыхания, диссимиляции в клетке увеличивают ее энтропию d_iS>0. В зависимости от соотношения скоростей изменения d_eS и d_iS общая энтропия dS открытой системы может либо увеличиваться, либо уменьшаться со временем. Если единственной причиной необратимости и увеличения энтропии системы являются ее внутренние процессы, то они ведут к уменьшению ее термодинамического потенциала. В этом случае

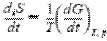
где G - полный термодинамический потенциал (или энергия Гиббса G = U + PV - TS).

Энергетическую характеристику открытой биологической системы в соответствии со вторым принципом термодинамики можно дать на основе баланса (обмена) энтропии. Это впервые сделал бельгийский ученый, лауреат Нобелевской премии И. Пригожин. Если обозначить dS /dt - скорость изменения энтропии открытой системы, d_iS/dt - скорость образования энтропии в системе за счет внутренних необратимых процессов, d_eS/dt – скорость обмена энтропией с внешней средой, то уравнение Пригожина имеет вид
dS/dt = dS_i/dt + dS_e/dt

причем член dS_i/dt по определению, всегда положителен, а член d_eS/dt может быть как положительным, так и отрицательным. Таким образом, это изящное уравнение в лаконичной и обобщенной форме выражает суть энергетических процессов, происходящих в открытой биологической системе.
Стационарным называется такое состояние открытой систе­мы, при котором основные макроскопические параметры систе­мы остаются постоянными.
Термодинамическим критерием (условием) стационарного со­стояния является равенство между продукцией энтропии орга­низмом и потоком энтропии из него в окружающую среду:

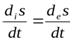
а полное изменение энтропии равно нулю:

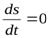(21)

Понятно, что термодинамическому равновесию свойственно отсутствие потока веществ между системой и средой, тогда как стационарное состояние открытой системы поддерживается бла­годаря обмену веществом и энергией со средой. Именно в ок­ружающей среде открытая система черпает свободную энер­гию, необходимую для поддержания стационарного состояния. Для сохранения термодинамического равновесия затрачивать свободную энергию не нужно,
В биологической системе термодинамическое равновесие ус­танавливается только при наступлении смерти. В обычных ус­ловиях жизни организм поддерживает стационарное состояние, которое характеризуется не отсутствием процессов, а таким ихтечением (обычно весьма активным и напряженным), при ко­тором они сбалансированы настолько, что основные параметры системы сохраняются неизменными, создавая внешнее впечат­ление «покоя».

Не существует какой-либо связи между величиной химического сродства и скоростью реакции. Реакции между веществами с большим химическим сродством могут протекать медленно, и наоборот, вещества с малым химическим сродством могут реагировать очень быстро. Так, согласно термодинамике, смесь газообразных водорода и кислорода при обычной температуре должна практически полностью превращаться в воду (для этой реакции DG^o = –450 кДж), однако в эксперименте образование воды практически не наблюдается. Химический потенциал алмаза в обычных условиях больше химического потенциала графита и, следовательно, алмаз должен самопроизвольно превращаться в графит, в действительности же такое превращение не происходит.
Такое кажущееся противоречие между теоретическими предсказаниями и практическими результатами обусловлено тем, что в термодинамике учитывается только начальное и конечное состояния системы, но не рассматривается механизм перехода и не фигурирует такой практически важный фактор как время. Реально всякое превращение связано с преодолением некоторого энергетического барьера – разрыв связей в молекулах реагирующих веществ, перестройка структуры кристаллической решетки и т.д. Если энергетический барьер высок, то теоретически возможная реакция протекает настолько медленно, что за практически ограниченный промежуток времени каких-либо изменений не наблюдается (реакция “не идет”).

Таким образом, кроме термодинамического подхода, громадное значение приобретает и другой аспект исследования химических реакций – изучение их с точки зрения скоростей

Следствием первого закона термодинамики является закон Гесса, утверждающий, что тепловой эффект реакциине зависит от пути реакции, а только от начального и конечного состояний.
17.Понятие обобщенных сил и потоков. Линейные соотношения и соотношения взаимности Онзагера. Стационарное состояние и условия минимума скорости прироста энтропии. Теорема Пригожина. Осуществление принципа Ле-Шателье в стационарных состояниях.
Обобщенные потоки и термодинамические силы могут быть связаны так называемыми соотношениями Онзагера. Эта связь ограничивается принципом Кюри, запрещающим взаимную связь явлений различной тензорной размерности.
Обобщенные потоки зависят от обобщенных сил, и наоборот - скорость химической реакции зависит от сродства, поток тепловой энергии - от разности температур.
Обычно обобщенные потоки определяются предыдущей историей образца.
Координаты обобщенных потоков и обобщенных термодинамических сил связаны между собой с помощью феноменологических коэффициентов.
Обобщённые потоки зависят от обобщённых сил (поскольку ими вызываются), и наоборот – скорость химической реакции зависит от сродства, поток тепловой энергии – от разности температур
Обобщённая сила — величина коэффициента при вариации обобщённой координаты в слагаемом выражения для виртуальной работы, относящимся к обобщённой координате.

Cоотношение Онзагера: Все термодинамические процессы характеризуются собственными значениями потока, скорости и движущей силы. Однако если в системе одновременно протекает несколько термодинамических процессов, процессы могут взаимодействовать друг с другом. В результате скорость каждого из них, иными словами, поток каждого термодинамического параметра будет зависеть не только от «своей» термодинамической силы, но и от движущих сил всех других процессов, происходящи в системе. Впервые принцип взаимодействия термодинамических процессов был выдвинут в 1931 году Л. Онзагером. Таким образом, уменьшение числа независимых феноменологических коэффициентов, необходимых для количественного описания неравновессных систем, достигается применением соотношения взаимности Онзагера. Согласно этому принципу многие взаимодействующие необратимые процесы могут быть описаны линейным дифференциальным уравнением с постоянными коэффициентами:

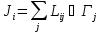, (11)

Где 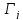– интенсивные термодинамические параметры (T, P, µ и т.д.), 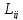-соответствующие коэффициенты, не зависящие от значения градиентов 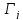, т.е. термодинамических сил 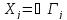. Соотношение взаимности Онзагера показывает, что если поток необратимого процессаi испытывает влияние термодинамической силы 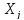необратимого процессаj через посредство коэффициента 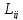, то и поток процессаj также испытывает влияние термодинамичесой силы 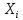через посредство того же самого коэффициента 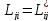. Данный принцип оказался очень плодотворным при рассмотрении многих необратимых процессов вблизи термодинамического равновесия ситемы, а сооотношение 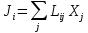в общем виде получили наименование линейных феноменологических уравнений взаимности Онзагера. При этом взаимодействующие термодинамические процессы называются сопряженными.Cоотношения взаимности Онзагера играют важную роль в термодинамике неравновесных процессов и, кроме того, находят непосредственное использование в анализе некоторых свойств мембранных, каталитических и биологических систем вблизи термодинамического равновесияю. Так, используя эти отношения и экспериментально определяя значения коэффициентов 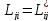, можно установить количественную взаимосвязь между одновременно протекающими в системе процессами даже в отсутствие детальной информации о механизме рассматриваемых процессов.

Теорема Пригожинаутверждает, что скорость продукции энтропии

внутри открытой системы в стационарном состоянии положительна и минимальна.

Она характеризует эволюцию открытой системы вблизи равновесия.

Следствие теоремы ПригожинаэтоПринцип Ле-Шателье. Если термодинамическую систему вывести из

состояния равновесия, в ней возникнут силы и потоки, стремящиеся вернуть

систему в исходное состояние равновесия.
18.Границы применимости линейной термодинамики в биологии. Критерий Удаленности сложных биологических процессов и их отдельных стадий от термодинамического равновесия. Нелинейная термодинамика. Общие критерии устойчивости стационарных состояний и перехода к ним вблизи и вдали от равновесия. Связь между кинетикой и термодинамикой.

Линейная термодинамика описывает стабильное, предсказуемое поведение систем, стремящих­ся к минимальному уровню активности, совместимому с питающими их потоками. Из того, что линейная нерав­новесная термодинамика так же, как и равновесная тер­модинамика, допускает описание с помощью потенциала, а именно производства энтропии, следует, что и при эво­люции к равновесию, и при эволюции к стационарному состоянию система «забывает» начальные условия. Ка­ковы бы ни были начальные условия, система рано или поздно перейдет в состояние, определяемое граничными условиями. В результате реакция такой системы на лю­бое изменение граничных условий становится предска­зуемой.

Второй закон термодинамики - опытный закон, установленный для замкнутых земных макросистем. В случае галактических систем определяющую роль в их поведении начинают играть дальнодействующие гравитационные силы, и такие системы уже нельзя считать замкнутыми. Этим определяется верхняя граница применимости второго закона: он неприменим к достаточно большим участкам Вселенной.
Между тем, некритическое перенесение закономерностей земного макроскопического опыта на Вселенную как целое приводило к антинаучным выводам о так называемой "тепловой смерти Вселенной", сделанным рядом физиков и философов в прошлом столетии. Распространяя действие второго закона на всю Вселенную, Р.Клаузиус пришел к выводу, что энтропия Вселенной стремится к максимуму. Следовательно, все виды движения во Вселенной должны самопроизвольно перейти в тепловое хаотическое движение, температура всех тел во Вселенной выравняется и наступит состояние "тепловой смерти" - в результате этого исчезнут причины, способствующие возникновению каких бы то ни было процессов.
Ошибочность подобных рассуждений заключалась в том, что Вселенной неправомерно приписывались свойства замкнутой системы. Кроме того, Вселенная непрерывно развивается, примерами чего могут служить ее расширение (данные астрофизики и космологии) и образование новых звездных систем. Для Вселенной само понятие термодинамического равновесия лишено смысла, поэтому для нее не существует состояния максимальной энтропии. Энтропия Вселенной в каждой ее области может возрастать неограниченно без приближения к состоянию максимальной энтропии, то есть к "тепловой смерти".
Таким образом, второй закон термодинамики применим только к изолированным термодинамическим системам.

Условием термодинамического равновесия всложных изолированных однородных системах является одинаковость температур, давлений и обобщенной силы Условия фазового равновесия дополняются условием равенства обобщенных сил в сосуществующих фазах. Следует иметь в виду, что выражение для химического потенциала сложной системы имеет вид.

В последние годы были развиты основы термодинамики сильно неравновесных систем, в которых связь между термодинамическими потоками и силами перестает быть линейной, а также не выполняется соотношение взаимности Онсагера.
Это направление, получившее название нелинейной термодинамики, приводит к возможности спонтанного возникновения упорядоченных структур в различных сильно неравновесных открытых системах, т.е. к процессу самоорганизации.
Общим во всех явлениях образования упорядоченных структур при необратимых процессах в сильно неравновесных открытых системах является совместное (кооперативное) движение больших групп молекул. Немецкий ученый Г.Хакен предложил дл