Химическая система. Функция состояния системы. Внутренняя энергия системы. Работа и теплота. Изменение внутренней энергии системы в ходе химических превращений.

Химическая система – это совокупность веществ, находящихся во взаимодействии и мысленно выделенная из окружающей среды.

В зависимости от характера взаимодействия системы с окружающей средой различают открытые, закрытые и изолированные системы.

Открытой системой называется система, которая может обмениваться с окружающей средой энергией и массой (веществом). Примером открытой системы может служить живой организм и стакан горячего чая.

Закрытой системой называется система, которая может обмениваться с окружающей средой только энергией. В качестве примера закрытой системы можно привести невскрытую банку консервов.

Изолированной системой называется система постоянного объема, в которой не происходит обмена с окружающей средой ни массой, ни энергией. Привести пример изолированной системы затруднительно, т. к. даже Солнечная система является изолированной лишь в первом приближении. В какой-то мере такой системой можно считать закрытый сосуд Дьюара.

Часть системы, отделенная от других ее частей хотя бы одной поверхностью раздела, называется фазой.

Система, состоящая из веществ, находящихся в одной фазе, называется гомогенной.

Система, состоящая из веществ, находящихся в разных фазах и имеющих хотя бы одну поверхность раздела, называется гетерогенной. Например, лед и вода (жидкость) в одном сосуде – гетерогенная двухфазная система.

Компонентом системы называется вещество, которое может быть выделено из системы и существовать вне ее.

Состояние системы определяется ее параметрами. Параметры системы могут быть заданы на молекулярном уровне (координаты, количество движения каждой из молекул, очередность обмена молекул положениями в пространстве, энергией и др. – микроскопические параметры) и на уровне описания состояния всей системы (макроскопические параметры). Любому макроскопическому состоянию системы отвечает множество различных положений и движений молекул, т.е. множество микроскопических состояний. Макроскопических параметров, в отличие от микроскопических, немного, что очень удобно для их практического применения. Параметры состояния системы — это величины, позволяющие определить состояние системы, непосредственно измерив эти величины. В химии чаще всего используются следующие параметры состояния: давление, температура, объем, концентрация и др.

Различают:

ü экстенсивные параметры состояния, пропорциональные количеству вещества системы: масса, объем,

ü внутренняя энергия и т. п.,

ü интенсивные параметры состояния, не зависящие от количества вещества системы: давление, температура, вязкость и т. п.

Набор параметров системы называется состоянием системы. Изменение состояния системы называется процессом.

Различают следующие процессы:

ü изохорный – процесс, протекающий без изменения объема системы (V = const),

ü изобарный – процесс, протекающий без изменения давления в системе (p = const),

ü изотермический – процесс, протекающий без изменения температуры в системе (T = const),

ü адиабатный – процесс, протекающий без поглощения и выделения системой теплоты (Q = 0).

Процесс называется обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы называется необратимым.

Важными понятиями термодинамики являются: энергия, теплота и работа.

Энергия — общая количественная мера движения и взаимодействия всех видов материи. В соответствии с различными формами движения материи энергию разделяют на механическую, электромагнитную, ядерную, тепловую, и т. д. Это деление до известной степени условно.

Теплота (Q) — форма беспорядочного (теплового) движения образующих тело частиц (молекул, атомов, электронов и т. д.). Количественной мерой теплоты служит количество теплоты, т. е. количество энергии, получаемой или отдаваемой системой при теплообмене. Теплота измеряется в единицах энергии: Дж, кал (1кал = 4,184Дж).

Работа (А) — произведение обобщенной силы на обобщенную координату. Механическая работа представляется произведением силы на перемещение. Электрическая работа рассматривается как произведение заряда на разность потенциалов. Работа расширения идеального газа равна произведению давления на изменение объема. Здесь сила, давление, разность потенциалов — обобщенная сила, а перемещение, изменение объема, заряд — обобщенная координата.

Теплота и работа являются эквивалентными формами передачи энергии.

Состояние системы определяется различными функциями, называемыми функциями состояния.

Функция состояния — функция независимых параметров системы, изменение которой не зависит от пути перехода системы из начального состояния в конечное, а зависит только от состояния системы в этих точках.

Разделение переменных на параметры состояния и функции состояния достаточно условно, так как в данном случае если X является функцией Y, справедливо и обратное утверждение. За параметры состояния приняли величины, абсолютное значение которых можно непосредственно измерить. Для функции состояния можно измерить или рассчитать лишь ее изменение (Δ). Изменение функции состояния рассматривается как разность ее значений в конечном и исходном состояниях системы, например,

ΔХ = Х₂ - Х₁ [1]

Индексы «1» и «2» характеризуют начальное и конечное состояния системы, соответственно.

Внутренняя энергия (U) — энергия системы, зависящая от ее внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т. д.), энергию колебательных и вращательных движений атомов в молекулах и энергию взаимодействия этих частиц, т. е. полный запас энергии в веществе. Естественно, измерить и рассчитать абсолютное значение внутренней энергии невозможно, можно лишь с достаточной точностью измерить ее изменение. Это характерно для всех функций состояния системы. Поскольку для нахождения изменения функций состояния и сравнения их между собой необходим единый уровень отсчета, то ввели понятие стандартного состояния вещества (системы). Стандартное состояние выбирают из соображений удобства расчетов; оно может меняться при переходе от одной задачи к другой. Значения термодинамических величин в стандартном состоянии называют стандартными и обозначают обычно с «нулем» в верхнем индексе, например, Н°, G°. Для химических реакций ΔG⁰, ΔН⁰ равны изменениям соответствующих G, Н реагирующей системы в процессе перехода от исходных веществ, находящихся в стандартном состоянии, к продуктам реакции, находящимся в стандартном состоянии.

Одно из возможных стандартных состояний характеризуется стандартными условиями: давлением (р°), составом (молярная концентрация с°): р° = 101325 Па = 1 атм; с° = 1 моль/л (С_М)

Система знаков. В эксперименте или в расчетах получают изменения функций состояния. Они могут принимать как положительные, так и отрицательные значения. В термодинамике для обозначения обмена энергией между системой и внешней средой принята следующая система знаков: энергия, получаемая системой от внешней среды, обозначается знаком «плюс», а отданная системой — знаком «минус».

+ Q — теплота, поглощенная системой;

- Q — теплота, выделенная системой;

- А — работа, совершенная системой против внешних сил;

+А — работа, совершенная внешними силами над системой.

Анализ тепловых явлений базируется на трех фундаментальных принципах (законах), подтвержденных данными многочисленных наблюдений.

Первое начало термодинамики. Энтальпия. Изменение энтальпии в ходе химического процесса. Закон Гесса, следствие из закона Гесса. Стандартная энтальпия образования вещества.

Первое начало термодинамики: Суть первого закона термодинамики заключается в том, что тела могут обмениваться между собой энергией в виде тепла и работы, при этом энергия не исчезает и не возникает ниоткуда. Отсюда видно, что этот закон представляет собой одну из форм закона сохранения энергии.

Пусть какая-то система совершает круговой процесс, последовательно переходя из исходного состояния в состояния I, II, III и т. д. В конечном итоге она возвращается в исходное состояние с начальными значениями всех своих параметров. Предположим, что система в этом процессе поглотила теплоту Q совершила работу А. Т. к. в самой системе ничего не изменилось, согласно закону сохранения энергии Q + А=0.

Рассмотрим другой вариант: система совершает незамкнутый процесс, переходя из состояния I в состояние II. При этом она поглощает теплоту Q совершает работу А. В общем случае состояния I и II могут отличаться значениями своих параметров, т. е. в самой системе могли произойти какие-то изменения, и в общем случае сумма количества теплоты, поглощенного системой, и работы, которую внешняя среда совершила над системой при этом, не равна нулю и приводит к изменению внутренней энергии: DU = Q+А [2]

Основываясь на этой формуле можно дать следующую формулировку первого начала термодинамики:

Количество энергии, которое выделяется или поглощается в форме теплоты и работы, равно изменению внутренней энергии.

Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.

1) Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.

2) Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход.

Первый закон (первое начало) термодинамики можно сформулировать так: «Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённого системе, в сумме с работой A', совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил»: ΔU = Q − A + A' [3]

Формулы [2] и [3] является математической записью первого закона термодинамики.

Если δQ > 0, то это означает, что тепло к системе подводится.

Если δQ < 0, аналогично — тепло отводится.

Если δQ = 0, то систему называют адиабатически изолированной.

Теплота реакции и энтальпия: Различные химические реакции могут протекать как при постоянном объеме, так и при постоянном давлении. Определим, изменению каких функций состояния соответствуют при этом их тепловые эффекты.

Пусть система совершает работу только против сил внешнего давления, тогда изменение внутренней энергии будет равно:

DU=Q - рDV, [3], где р — внешнее давление, а DV— изменение объема. Произведение рDV = - А —работа.

Если реакция протекает при постоянном объеме, то изменение объема равно нулю, следовательно, произведение pDV = 0. Таким образом, тепловой эффект химической реакции, протекающей при постоянном объеме, равен изменению внутренней энергии системы: Q_v = DU.

Индекс «V» обозначает, что реакция протекает при постоянном объеме.

Рассмотрим, чему будет равен тепловой эффект реакции при постоянном давлении. В этом случае уравнение [3] примет вид: U₂ - U₁ = Q_p – pּ(V_{2 –} V₁). [5]

Отсюда Q_р = (U₂+p V₂) - (U₁ + pV₁). [6]

Параметры системы подпадают под определение функции состояния, так как их изменение зависит только от значений в начальном и конечном состояниях системы. Поэтому произведение давления на объем будет функцией состояния системы, а сумма этого произведения с внутренней энергией также будет представлять функцию состояния, которая называется энтальпией (H): H = U + pV. (7)

Тепловой эффект реакции при постоянном давлении можно представить в виде изменения свойства системы, т. е. Q_Р = Н₂ –Н₁ =DН, [8], где H₁ — энтальпия исходных веществ, а H₂ — энтальпия продуктов реакции. Иными словами, Q_p, так же как и Q_v, не зависит от пути протекания реакции.

Из уравнений [4] и [5], учитывая уравнение Менделеева-Клапейрона: РV = νRТ, [9] – получим соотношение между тепловыми эффектами реакций между идеальными газами, протекающих при постоянных давлении и объеме:

Q_p = Q_v + νRT. [10]

Теплоемкость— количество теплоты, поглощаемое телом при нагревании на 1 градус (1°С или 1 К).

Теплоемкость единицы массы вещества называют удельной теплоемкостью [Дж/кг • К]

Теплоемкость 1 моля вещества — молярная (мольная) теплоемкость [Дж/моль • К].

Количество теплоты, поглощенное телом при изменении его состояния, зависит не только от начального и конечного состояний, но и от условий перехода между ними. Различают теплоемкость при постоянном объеме (С_ν) и теплоемкость при постоянном давлении (С_р). При постоянном давлении нагревание приводит к тому, что часть теплоты идет на совершение работы расширения тела, а часть — на увеличение его внутренней энергии, тогда как при нагревании при постоянном объеме вся теплота расходуется на увеличение внутренней энергии.

Для идеальных газов: С_р = С_ν+R. [11]

По знаку теплового эффекта реакции делятся на: эндотермические— реакции, протекающие с поглощением тепла, и экзотермические— реакции, в результате которых тепло выделяется.

Запись термохимических уравнений отличается от записи уравнений химических реакций. При написании термохимических уравнений реакций необходимо указать дополнительную информацию:

а) для всех участников процесса — и для реагентов (веществ, вступивших в реакцию), и для продуктов (веществ, образовавшихся в результате реакции), используя нижние индексы, указывают их агрегатные состояния:

«к» — кристаллическое (иногда «т» – твердое) ;

«ж» — жидкое;

«г» — газообразное;

«р» — раствор.

б) в правой части уравнения указывают тепловой эффект реакции. Например:

2 Na_К + Н₂О_Ж = 2 NaОН _Р + Н_{2 Г} + 368 кДж

В термохимических таблицах обычно приводятся тепловые эффекты реакций при постоянном давлении, которые обозначаются

D_rH⁰_T, где нижний индекс Т соответствует температуре, к которой относится данное значение теплового эффекта (обычно для Т= 298 К). Верхний индекс «°» означает, что все участники реакции находятся в стандартных состояниях. Этот тепловой эффект реакции называют изменением энтальпии реакции или чаще просто энтальпией реакции. Экспериментальным определением тепловых эффектов различных реакций занимается раздел химии, называемый термохимией.Найденные величины составляют основы справочников. С их помощью можно рассчитать тепловые эффекты других реакций, даже тех, которые провести экспериментально невозможно. Для этого необходимо составить цикл из термохимических реакций, которые можно осуществить экспериментально и результатом сложения которых является искомая реакция. Для составления подобных термохимических циклов необходимо познакомиться с важнейшими определениями, приведенными ниже.

Стандартная теплота (энтальпия) образования соединения: Эта величина является одной из ключевых величин в термодинамике.

Стандартной энтальпией образованияхимического соединения называют стандартное изменение энтальпии в результате реакции образования 1 моля этого вещества из простых веществ, взятых в том агрегатном состоянии, в котором они находятся при стандартных условиях и данной температуре.

Стандартные энтальпии образования простых веществ (рассматриваются аллотропные формы, устойчивые при стандартных условиях и Т = 0⁰ К) принимаются равными нулю. Для обозначения стандартной энтальпии образования соединения принята следующая форма записи: D_fH⁰₂₉₈ (KNO₃), где буква f — первая буква английского слова fогтаtion — «образование», значения верхнего и нижнего индексов при ∆Н см. 1.3.1. Для KNO₃ стандартная энтальпия образования соответствует изменению энтальпии в реакции:

К_к + 0,5 N_2,г +1,5 О₂,_г = КNО₃,к.

Энтальпия образования измеряется в единицах кДж/моль.

Стандартная энтальпия сгорания: Эта величина чаще всего определяется при термохимических измерениях в калориметрах (специальных приборах).

Стандартной энтальпией сгоранияназывается энтальпия реакции сгорания вещества в кислороде с образованием оксидов элементов, имеющих высшую степень окисления, или простых веществ, если они более устойчивы в данных условиях, чем оксиды.

Примерами могут служить следующие реакции:

СН₄,_Г + 2 О₂,_г = 2 Н₂О_Ж + СО₂,_Г

NH₃,_г + 1,5 О₂,_г = 0,5 N_2,r + 1,5 Н₂О_ж

Стандартная энтальпия химической связи—это изменение энтальпии в реакции образования одного моля двухатомных молекул (или других двухатомных частиц) из атомов веществ, находящихся в газообразном состоянии:

Н_г + Сl_г = НС1_г

С_г + Н_г = СН_г

Образование химической связи — процесс экзотермический, и поэтому энтальпия его всегда имеет отрицательное значение. Энтальпия обратной реакции, соответствующая реакции диссоциации двухатомной молекулы (частицы), называется энтальпией разрыва связи. В этом случае процесс эндотермический, и она имеет положительное значение.

Для двухатомных молекул энтальпия разрыва связи определяется как энтальпия диссоциации. Для многоатомных молекул эта величина является условной и отвечает энтальпии такого процесса, при котором данная химическая связь разрывается, а все остальные связи остаются без изменения. Реально для многоатомных молекул можно определить лишь среднее значение энтальпии разрыва химической связи, потому что энтальпии последовательных разрывов связей в них не равноценны. Например, энтальпия отрыва первого атома водорода от молекулы метана не равна энтальпии отрыва второго и т. д.

Химические связи условно подразделяют на прочные, или сильные — энергия разрыва связи > 500 кДж/моль; слабые от ~ 100 до ~ 20 кДж/моль, водородные ~ 15 кДж/моль. Межмолекулярные (ван-дер-ваальсовы) силы имеют энергию связи ~ 5 кДж/моль и менее.

Стандартная энтальпия сублимации (испарения)равна стандартному изменению энтальпии при переходе одного моля твердого (жидкого) вещества в газообразное состояние. Так как большинство металлов переходит в газ в атомарном состоянии, для металлов эту величину еще называют энтальпией атомизации.

Стандартная энтальпия плавленияравна стандартному изменению энтальпии при переходе одного моля вещества из твердого состояния в жидкое. Принята следующая форма записи этих величин: D _sН°, D_ν H⁰ и D_тН°. Буквы s, ν и т являются первыми буквами английских слов sиbliтаtion — «сублимация (возгонка)», vароrization — «испарение» и теlting — «плавление».

Закон Гесса: В основе всех термохимических расчетов лежит закон Гесса: Тепловой эффект химической реакции зависит только от начального и конечного состояний системы и не зависит от пути перехода (от промежуточных состояний).

Этот закон справедлив для реакций, протекающих либо: при постоянном объеме — в этом случае тепловой эффект реакции равен изменению внутренней энергии системы,

либо при постоянном давлении.

Первое следствие из закона Гесса — тепловой эффект химической реакции равен изменению энтальпии, т. е. разности между алгебраическими суммами энтальпий образования продуктов и исходных веществ: D_rH⁰₂₉₈ = ∑v_i · D_fH⁰_298,i - ∑_vj ·D_fH⁰_298,j

где D_rH⁰₂₉₈ — теплота реакции, r — первая буква слова rеасtiоп, ν_i, и νj — количества (молей) веществ, вступивших в реакцию, и продуктов реакции. Размерность энтальпии реакции — кДж.

С помощью закона Гесса можно определить энтальпии образования веществ, которые невозможно измерить непосредственно, например, глюкозы. Действительно, осуществить в калориметре реакцию образования глюкозы из простых веществ: 6С_к + 6Н_2,r + 3О₂,_r = С₆Н₁₂О₆,_к

невозможно, а измерить экспериментально тепловой эффект реакции ее сгорания довольно легко:

С₆Н ₁₂О₆,_К + 6 О₂,_г = 6 СО₂,_r + 6 Н₂О_ж

Тепловой эффект этой реакции, согласно закону Гесса, определяется уравнением:

D_rH⁰₂₉₈ = 6D_fH⁰_298, CO₂+6D_fH⁰_298, H₂O - D_fH⁰_298,C₆H₁₂O₆

Из этого уравнения можно определить энтальпию образования глюкозы:

D_fH⁰_298,C₆H₁₂O₄ = 6D_fH⁰_298, CO₂ + 6D_fH⁰_298, H₂O - D_rH⁰₂₉₈

Энтальпии образования воды и углекислого газа определены экспериментально и занесены в справочные таблицы, тепловой эффект реакции сгорания глюкозы определяют экспериментально.

Другим примером применения закона Гесса может служить нахождение энтальпии образования этилена.

Известны энтальпии реакций: гидрирования этилена (—136,8 кДж/моль), сгорания этана (— 1559,8 кДж/моль), и энтальпии образования углекислого газа и воды:

D _f H⁰ ₂₉₈,CO_2г = -393,3 кДж/моль,

D _f H⁰ ₂₉₈, H₂O_ж = -285,8 кДж/моль.

Запишем термохимический цикл из указанных реакций таким образом, чтобы их суммой явилась реакция образования одного моля этилена:

2С_Г + 2О₂,_Г = 2СО₂,_Г D_rH⁰₂₉₈ = 2 ·(-393,3) =-786,6 кДж

ЗН₂,_г+1,5О ₂,_r = ЗН₂О_ж D_rH⁰₂₉₈ = 3-(-285,8) =-857,4кДж

С₂Н_6Г = С₂Н₄,_Г + Н_2,г D_rH⁰₂₉₈ = + 136,8 кДж

2 С0₂,_г + 3 Н₂0_Ж = С₂Н₆,_Г + 3,5 0₂,_г D_rH⁰_{298 =} + 1559,8 кДж

2 С_гр. + 2 Н_2,г = С₂Н_4,Г D_rH⁰₂₉₈ = + 52,6 кДж.

Т. к. реакция записана для одного моля С₂Н₄, то D_rH⁰₂₉₈ С₂ H₄ = 52,6 кДж/моль.

Записи термохимического уравнения реакции в виде:

2 Na_К + 2Н₂О_Ж = 2 NaОН _Р + Н_{2 Г} Δ _r H = -368 кДж

означает, что при взаимодействии двух молей натрия и двух молей воды выделится 368 кДж энергии.

Второе следствие из закона Гессам – Термохимические уравнения можно складывать и вычитать также как алгебраические. Например, тепловой эффект (энтальпия) двухстадийной химической реакции равен сумме тепловых эффектов (энтальпий) каждой стадии:

1-ая NaOH_водн. + H₂SO_4,водн. = NaHSO_4,водн. + H₂O_ж, ΔrH₁ = -61,7 кДж

2-ая NaOH_водн. + NaHSO_4,водн. = Na₂SO_4,водн. + H₂O_ж, ΔrH₂ = -69,7 кДж.

Складываем правые и левые части уравнений, а также тепловые эффекты обеих стадий

NaOH_водн. + H₂SO_4,водн. + NaOH_водн. + NaHSO_4,водн. = NaHSO_4,водн. + H₂O_ж + Na₂SO_4,водн. + H₂O_ж, ΔrH₁ + ΔrH₂ = -61,7 + (-69,7) = -131,4 кДж.

Получаем после объединения формул одинаковых веществ, находящихся в одной части полученного уравнения и вычитания, находящихся в разных частях:

2NaOH_водн. + H₂SO_4,водн. = Na₂SO_4,водн.+ 2H₂O_ж, ΔrH₃ = -131,4 кДж

Тепловые эффекты прямой и обратной реакции равны по величине и обратны по знаку:

2H_2,г+ O_2,г = 2H₂O_ж, Δ_rH = -571,6 кДж

2H₂O_ж = 2H_2,г+ O_2,г, Δ_rH = +571,6 кДж

Факторы, определяющие направление самопроизвольного протекания химических процессов (энергетический и энтропийный). Энтропия. Второе и третье начала термодинамики. Определение изменения энтропии в ходе реакции.

Второй закон (начало) термодинамики: Ограниченность первого начала термодинамики заключается в том, что оно не определяет направления обмена тепловой энергией между телами. Первое начало не запрещает переход тепла от менее нагретого тела к более нагретому. Суть второго начала состоит в том, что оно определяет направление самопроизвольного протекания процессов, в том числе и химических реакций.

Самопроизвольнымназывается процесс, который протекает самостоятельно без воздействия внешних факторов. Например, если соединить два сосуда — заполненный газом и пустой, то газ самопроизвольно заполнит весь объем. Взаимодействие металлического натрия с водой при н. у. также происходит самопроизвольно. Обратные процессы можно осуществить, оказав внешнее воздействие. Для исследователя необходимо иметь критерий, с помощью которого можно было бы предсказать направление самопроизвольного протекания процесса.

Существует еще одна функция состояния, которая с учетом первого начала термодинамики позволяет предсказать направление протекания процесса в изолированных системах. Такой функцией состояния является энтропия(S). Интерпретировать энтропию можно как с точки зрения макроскопического состояния системы, так и с точки зрения микроскопического.

Третье начало термодинамики: Еще один важный принцип химической термодинамики был установлен в первой четверти 20 в. В. Нернстом. Он экспериментально установил, что, когда температура приближается к абсолютному нулю, стандартные энтропии DS° для многих химических реакций стремятся к нулю. Поскольку этот результат не следует из первого и второго начал термодинамики, он получил название третьего начала термодинамики. Оно не имеет столь же общего характера, как первые два начала, однако большинство очевидных исключений или аномалий получило удовлетворительное объяснение с учетом особенностей кристаллического строения конкретных веществ.
Значение принципа Нернста состоит в том, что зависимость энтропии реакции от температуры может быть выведена, согласно термодинамической теории, исключительно из данных по теплоемкости для отдельных участвующих в реакции веществ. Это значит, что, если известно значение DS° при какой-либо одной температуре (при T = 0 DS° = 0), значения энтропии реакции при других температурах вычисляются исключительно из тепловых измерений. Аналогично этому, величина DH° может быть получена из калориметрических данных путем непосредственного измерения теплоты данной реакции либо косвенно, путем измерения теплот других реакций и применения закона Гесса. Следовательно, подстановка полученных значений DH° и DS° в уравнение (9) или (11) дает гиббсову энергию или константу химического равновесия исключительно из тепловых измерений. Это позволяет предвидеть направление и равновесное состояние химической реакции еще до того, как найден способ ее проведения.
Для практического применения третьего начала термодинамики требуются точные результаты измерений теплоемкости вплоть до самых низких доступных температур, желательно до температуры жидкого гелия (около 4 К). Это направление термодинамических исследований химических явлений стимулировали криогенные исследования, выполненные в последние десятилетия.

Определение энтропии с позиций классической термодинамики: Если рассматривать систему в целом, то в обратимом процессе, протекающем при постоянной температуре, изменение энтропии будет равно: DS = 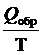[19]

Для необратимого процесса это равенство превращается в неравенство:DS > 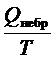[20]

Поскольку энтропия является функцией состояния, то ее изменение не зависит от пути перехода системы из одного состояния в другое, а определяется только значениями энтропии для системы в исходном и конечном состояниях. Размерность энтропии [S]=Дж/моль·К.

Существует много формулировок второго начала термодинамики. Приведем одну из них.

В изолированной системе самопроизвольно протекают только те процессы, которые сопровождаются увеличением энтропии.

В самопроизвольном процессе DS>0;

в равновесном процессе DS=0;

в не самопроизвольном процессе DS< 0.

В случае изотермического процесса для идеального газа изменение внутренней энергии равно нулю, отсюда, согласно уравнению [3]: Q_обр.= -А _расшр. [ 21 ]

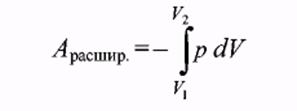[22]

Используя уравнение Менделеева-Клапейрона, получим: 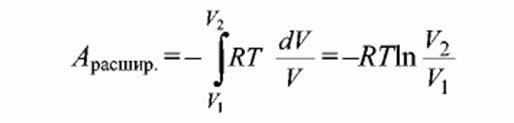[23]

Скомбинировав выражения [19], [21] и [23], получим для изменения энтропии в изотермическом процессе расширения одного моля идеального газа:DS=Rln 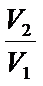[24]

Из определения С_р и уравнений [19] и [18] можно получить зависимость изменения энтропии от температуры: 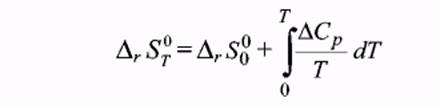[25]

или в частном случае, если АС_Р не зависит от температуры: DS = DАС_р-lп 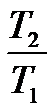[26]

Статистическая интерпретация понятия энтропии

Больцман вывел соотношение, связывающее абсолютную энтропию с числом микроскопических состояний системы, соответствующих данному макроскопическому состоянию (или термодинамической вероятностью): S = kּ1пW, [27]

Где k =R/N_A = 1,38 • 10²³Дж • К ^-1 — постоянная Больцмана, а W— число микроскопических состояний системы.

Макроскопическое состояние включает в себя множество микроскопических состояний. Их число для различных систем может подсчитываться по-разному. По Больцману макроскопическое состояние определяется количеством частиц на каждом энергетическом уровне. Частицы имеют свой номер, а полная энергия системы постоянна. Микроскопические состояния отличаются друг от друга распределением частиц по уровням энергий.

В термодинамике мы имеем дело с системами, состоящими из огромного числа частиц, с множеством макросостояний с различными W.

Из формулировки второго начала термодинамики следует, что в изолированной системе при самопроизвольном процессе энтропия возрастает. Система будет самопроизвольно стремиться к макросостоянию с максимальным W. Отсюда энтропию можно рассматривать как меру хаоса системы.

При абсолютной температуре Т = 0К чистые химические вещества образуют идеальные кристаллы, и их состояние можно описать только одним способом (W = 1), а логарифм единицы равен нулю. Согласно выражению [27], и энтропия при этой температуре равна нулю. Пользуясь этим, можно сформулировать третье начало термодинамики как: Энтропия химических веществ при абсолютном нуле равна нулю.

Таким образом, энтропия является единственной функцией состояния, для которой можно рассчитать абсолютное значение:

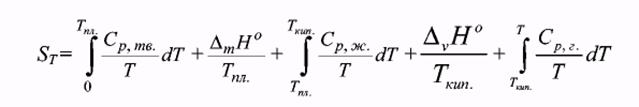
Второй закон термодинамики дает критерии для самопроизвольности протекания процессов (DS>0) и равновесия (DS = 0) в изолированных системах, которые практически не существуют. Можно применить второй закон термодинамики к неизолированным системам, поддерживаемым при постоянной температуре. Кроме того, предполагается, что система сохраняет постоянный объем или постоянное давление.

Направление протекания реакций: Рассмотрим возможность самопроизвольного протекания химической реакции в зависимости от знака энтальпийного и энтропийного членов в выражении изменения свободной энергии. Если изменение свободной энергии меньше нуля, то реакция протекает самопроизвольно. Если ∆G = 0, начальные и конечные состояния могут существовать в равновесии. Если же изменение свободной энергии больше нуля, самопроизвольное протекание реакции невозможно. Самопроизвольно протекает обратная реакция. А так как, согласно уравнению [32], изменение свободной энергии выражается через изменения энтальпии и энтропии (в предположении, что они не зависят от температуры), то их знаки будут определять знак ∆G. В ниже рассмотренных примерах принимается, что парциальные давления всех газообразных участников реакций равны по одной атмосфере, т.е. ∆G_г=∆G°_г. В этом случае можно использовать в расчётах стандартные изменения энтальпии и энтропии. Возможны четыре случая.

Первый:когда изменение энтальпии отрицательно, а изменение энтропии положительно, то изменение свободной энергии всегда отрицательно. Такие реакции самопроизвольно протекают в прямом направлении. Примером может служить реакция горения черного пороха, которая протекает по следующему суммарному уравнению:

2 КNO₃ + 3С + S =N₂ + ЗСО₂ + К₂S

Для этой реакции:

D_Г H⁰₂₉₈ = D _f H⁰₂₉₈ N₂ + 3D _f H⁰₂₉₈ CO₂ + D _f H⁰₂₉₈ K₂S - 2D _f H⁰₂₉₈ KNO₃ - 3D _f H⁰₂₉₈ C - D _f H⁰₂₉₈ S = - 582,41 кДж,

D_r S = S⁰₂₉₈N₂ + 3 S⁰₂₉₈ CO₂ + S⁰₂₉₈ K₂S - 2 S⁰₂₉₈ KNO₃ - 3 S⁰₂₉₈ C - S⁰₂₉₈ S = 630,34Дж/К

Следовательно,

D_rG⁰₂₉₈ = - 582,41-298ּ630,34ּ10^-3 = -770,25 кДж<0,

и реакция протекает самопроизвольно.

Второй:когда изменение энтальпии положительно, а изменение энтропии отрицательно. Эти реакции в прямом направлении самопроизвольно не идут, самопроизвольно протекает обратная реакция. В качестве примера приведем реакцию термического разложения хлористого водорода на простые вещества: 2 НС1_Г = Н₂,_г + С1₂,_г

Изменение энтальпии этой реакции равно двум энергиям разрыва связей Н—С1 и составляет 92,3 х 2 = 184,6 кДж. Изменение энтропии равно:D_rS⁰₂₉₈ = S⁰₂₉₈ H₂ + S⁰₂₉₈ Cl₂ - 2 S⁰₂₉₈ HCl = 130,6 + 233 - 2ּ186,7 = -19.8 Дж/К

D_rG⁰₂₉₈ = 184,6 - 298× (-19,8) ×10~³ = 190,5 кДж > О

Третий:когда как изменение энтальпии, так и энтропии отрицательны. В этом случае направление самопроизвольного процесса определяется температурой. При низкой температуре самопроизвольно идет прямая реакция, так как по абсолютной величине изменение энтальпии больше произведения температуры на изменение энтропии. Например, в реакции образования хлорида аммония из газообразных хлористого водорода и аммиака:

NН₃,г + НС1_Г =NH₄С1_К

D_гH⁰₂₉₈ = D_f H⁰₂₉₈ NH₄Cl - D_f H⁰₂₉₈ Cl₂ - D_f H⁰₂₉₈ NH₃ = -315,4-(-92,3)-(-46,2) = -176,9 кДж

D_r S = S⁰₂₉₈ NH₄Cl - S⁰₂₉₈ NH₃ - S⁰₂₉₈ HCl = 94,6 – 192,5 – 186,7 = -284,6 Дж/К

Т. к. при равновесии изменение свободной энергии равно нулю (DG = 0), то температура, при которой система находится в равновесии, равна 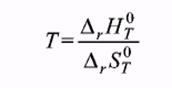[59]

И Т = 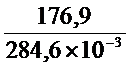= 621,6К

Четвертый:когда изменение энтальпии и энтропии положительные. Направление реакции также зависит от температуры: при низкой температуре самопроизвольно будет протекать обратная реакц