Гетерогенные равновесия в растворах электролитов. Произведение растворимости
Растворимость разных по природе веществ различается весьма сильно, от неограниченной, до пренебрежительно малой. Среди электролитов известны и те, и другие. Еще со школы нам знакомы «Таблицы растворимости солей и оснований», в которых относительная растворимость обозначена буквами «р» – растворим, «м» – малорастворим и «н» – нерастворим. Эти таблицы удобны для решения некоторых задач качественного характера, например, для определения возможности обменной реакции в результате связывания ионов в растворе, получения заданного электролита реакцией ионного обмена и др. Однако для количественной характеристики растворимости электролитов они малополезны. С их помощью невозможно определить, например, какой из двух «малорастворимых» электролитов менее растворим, можно ли из заданного малорастворимого электролита реакцией обмена получить другой малорастворимый или слабый электролит и т. д.
Абсолютно нерастворимых веществ не бывает. В этом нетрудно убедиться, проведя несложный эксперимент. Например, если хлорид серебра (обозначенный «н» в таблице растворимости) смешать с водой, дать отстояться осадку и в «воду» над ним добавить концентрированный раствор любого хорошо растворимого иодида (например, натрия, калия), то легко заметить выделение желто-оранжевого осадка иодида серебра. Откуда ионы серебра в растворе? Очевидно, из его хлорида, за счет частичного его растворения.
Из этого эксперимента также следует, что иодид серебра менее растворим, чем его хлорид. Можно ли эти результаты предсказать, не проводя эксперимента? Как рассчитать растворимость малорастворимого электролита и как увеличить или уменьшить её? Эти вопросы и рассматриваются ниже.
Обсуждая общие свойства растворов, мы отмечали, что «растворение» вещества – довольно сложный физико-химический процесс, и для насыщенных растворов малорастворимых веществ он равновесный. Следовательно, для него применимы те общие закономерности, которые мы ранее выявили для других равновесных процессов: закон действующих масс, принцип Ле Шателье и т.д.
Применение закона действующих масс к равновесию в насыщенном растворе малорастворимого электролита. Произведение растворимости
Равновесие в насыщенном растворе малорастворимой соли или основания можно условно представить следующей схемой:
MexАy¯ 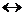 MexАy (р-р)
MexАy (р-р) 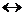 xMey+ + yАx–,
xMey+ + yАx–,
где MexАy¯ – осадок малорастворимой соли или основания, находящийся в равновесии с насыщенным раствором этого электролита (MexАy(р-р));
Mey+ – катионы, Аx– – анионы, на которые диссоциирует в растворе электролит.
Следует подчеркнуть, что в растворе электролит MexАy находится не в виде молекул, а в виде ионов; если электролитом является соль, то этот вывод очевиден (большинство солей – сильные электролиты); если электролит – слабое основание (Cu(OH)2, Fe(OH)3 и др.), практически полная их диссоциация обусловлена очень малой концентрацией (вспомните закон разбавления Оствальда). Таким образом, в равновесии с осадком малорастворимого электролита участвуют фактически его ионы, и поэтому равновесие обычно записывают в сокращенной (укороченной) форме:
MexАy¯ 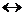 xMey+ + yАx–
xMey+ + yАx–
Применив закон действующих масс к такой гетерогенной системе, получим следующее выражение константы равновесия:
| К = (x∙[Mey+]x)×(y∙[Аx–]y) = ПР | (8.1) |
Эту константу называют произведением растворимости (ПР), и закон действующих масс применительно к таким равновесиям гласит:
В насыщенных растворах малорастворимых электролитов произведение равновесных молярных концентраций (активностей) ионов электролита – величина постоянная при постоянстве температуры и называется произведением растворимости.
Величины ПР малорастворимых электролитов при нормальных условиях (T = 298 K) приводятся в справочниках, например:
ПРAgCl = 1×10–10, ПРMg(OH)2 = 6×10–10, ПРAg2CrO4 = 1×10–12.
Произведение растворимости – это количественная характеристика равновесия растворения. При этом следует иметь в виду, что если рассмотренные ранее константы диссоциации и константы гидролиза однозначно позволяли сравнить, соответственно, силу нескольких слабых электролитов или гидролизуемость их солей, то связь произведения растворимости с растворимостью электролита более сложная. Для однотипных по составу электролитов такое сравнение возможно, например, для AgCl, BaCrO4, FePO4 (тип MeА) или для Ag2CrO4, CaF2, Mg(OH)2 (тип Me2B или MeB2): чем меньше ПР, тем меньше растворимость.
Однако если состав электролитов неоднотипный, то для них подобный вывод может оказаться и неверным. Например, для сульфида цинка произведение растворимости больше, чем для его фосфата (ПРZnS = 2×10–22, ПРZn3(PO4)2 = 1×10–32), но растворимость (моль/л, г/л) больше у второй соли (см. ниже уравнение (8.5) и пример 1).
Условие образования и растворения осадка малорастворимого электролита
Состояние равновесия является подвижным, и уравнение (8.1) соответствует состоянию системы, когда скорости реакций растворения и образования осадка равны. Если произведение молярных концентраций (активностей) ионов электролита в растворе больше, чем его ПР, то преобладающей будет скорость образования осадка; если большей величиной окажется ПР, то с большей скоростью будет протекать растворение осадка.
Таким образом, условием образования осадка малорастворимого электролита состава MexАy является следующее:
| C(Mey+)x×C(Аx–)y > ПР, | (8.2) |
а условием его растворения:
| C(Mey+)x×C(Аx–)y < ПР | (8.3) |
Избыточные ионы будут выделяться в виде осадка до тех пор, пока не выполнится условие: (x∙[Mey+]x)×(y∙[Аx–]y) = ПР.
Расчет растворимости малорастворимых электролитов
Расчет материального баланса в насыщенном растворе малорастворимого электролита выполняется аналогично расчетам для других равновесий (см. тему «Химическое равновесие»). Рассмотрим это на примере равновесия в насыщенном растворе некоторой малорастворимой соли MexАy:
MexАy¯ 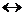 xMey+ + yАx––
xMey+ + yАx––
Обозначим концентрацию электролита в насыщенном растворе Р (моль/л); тогда равновесная концентрация катионов электролита будет x×Р и анионов – y×Р (моль/л). Подставив их в выражение ПР, получим:
| ПР = [Mey+]x× [Аx–]y = (xР)x× (yР)y = xx × yy × Р(x+y) | (8.4) |
Решая уравнение (8.4) относительно Р, получим формулу для расчета растворимости электролита:
Р = 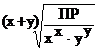 = [MexАy], моль/л = [MexАy], моль/л | (8.5) |
Тогда равновесные концентрации (моль/л) ионов в насыщенном растворе:
[Mey+] = 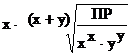 | (8.6) |
[Аx–] = 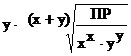 | (8.7) |
Из уравнения (8.5) видно, почему из сравнения ПР различных по составу электролитов не всегда очевидно соотношение их растворимостей: при разных x и y разными будут показатели корня для расчета Р.
На основании полученных уравнений несложно рассчитать растворимость электролита и концентрации ионов в других размерностях, встречающихся на практике (г/л, г/мл и т. д.).
Пример 1. Рассчитать растворимость (моль/л, г/л) ZnS и Zn3(PO4)2.
Решение
Напишем уравнения равновесий для насыщенных растворов этих солей и соответствующие им выражения ПР:
ZnS¯ « Zn2+ + S2– ПР = [Zn2+] × [S2–];
Zn3(PO4)2¯ « 3Zn2+ + 2PO43– ПР = [Zn2+]3 × [PO43–]2.
Преобразовав полученные выражения ПР как показано выше, получим:
для ZnS ПР = [Zn2+]×[S2–] = Р × Р = Р2,
для Zn3(PO4)2 ПР = [Zn2+]3× [PO43–]2 = (3Р)3× (2Р)2 = 27Р3×4Р2 = 108·Р5;
ПРZnS = 2·10–22, ПРZn3(PO4)2 = 1·10–32.
Рассчитаем растворимости этих солей:
РZnS = [Zn2+] = [S2-] = 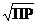 =
= 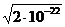 = 1,4×10–11 моль/л;
= 1,4×10–11 моль/л;
РZn3 (PO4)2 = [Zn2+]/3 = [PO43–]/2 = 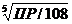 =
= 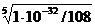 = 1,6·10–7 моль/л.
= 1,6·10–7 моль/л.
Растворимость тех же солей в г/л легко рассчитать, умножив Р на молярную массу соответствующей соли:
РZnS = 1,4 10–11 · 97,4 = 1,4·10–9 г/л;
РZn3(PO4)2 = 1,6·10–7 · 516,9 = 8,3 ·10–5 г/л.
Пример 2. Рассчитать растворимость (моль/л) Mg(OH)2.
Решение
Mg(OH)2¯ « Mg2+ + 2OH-, ПР =[Mg2+] · [OH–]2 = Р·(2Р)2 = 4·Р3 = 6·10–10,
Р = [Mg2+] = 1/2·[OH–] = 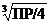 =
= 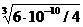 = 5,3·10–4 моль/л.
= 5,3·10–4 моль/л.
Смещение равновесий в насыщенных растворах электролитов. Влияние одноименных ионов на растворимость
Расчеты, приведенные ранее, справедливы для насыщенных растворов, ионный состав которых обусловлен только растворением индивидуального вещества(соли или основания). В этих случаях соотношение концентраций катионов и анионов в растворе однозначно определяется их соотношением в формульной единице («молекуле») электролита. Например, если электролитом является сульфид цинка, то концентрации его ионов в растворе равны [Zn2+] = = [S2–], а в растворе фосфата цинка соотношение молярных концентраций ионов [Zn2+]/[PO43–] = 3/2. Причем, эти соотношения не зависят от того, насыщенным или ненасыщенным будет раствор над осадком.
Однако, раствор, содержащий, например, ионы Zn2+ и PO43–, можно получить не обязательно растворением только фосфата цинка. Что произойдет при смешении растворов любой соли цинка, например, ZnCl2, и любой соли фосфорной кислоты, например, Na3PO4, в соотношениях совершенно произвольных, 1:1, 1:1000 или 1000:1 и др.?
– Если в полученном растворе произведение молярных концентраций ионов (в соответствующих степенях) не превысит величину ПР, т. е. если С3(Zn2+)×С2(PO43–) < ПР, то никаких изменений после сливания исходных растворов мы не заметим, осадка не будет.
– Если С3(Zn2+)×С2(PO43–) > ПР, то будет выделяться осадок. Причем, осадок фосфата цинка будет выпадать до тех пор, пока не выполнится условие:
С3(Zn2+)×С2(PO43–) = ПР
Очевидно, что при образовании осадка ионы Zn2+ и PO43– связываются друг с другом вполне определенно, в соотношении 3:2. Но какой при этом будет растворимость соли?
Пример 3. Как влияет на растворимость малорастворимого электролита увеличение концентрации ионов, участвующих в равновесии? Рассчитаем растворимость сульфида цинка в 0,1М растворе сульфида натрия.
Решение
До добавления Na2S концентрации ионов в насыщенном растворе ZnS были равными: [Zn2+] = [S2–] = 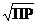 =
= 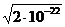 = 1,4×10–11 моль/л. После добавления Na2S, при его молярности С(Na2S) = 0,1 М, концентрация S2– увеличилась на столько же (см. Na2S ® 2Na+ + S2–).
= 1,4×10–11 моль/л. После добавления Na2S, при его молярности С(Na2S) = 0,1 М, концентрация S2– увеличилась на столько же (см. Na2S ® 2Na+ + S2–).
В соответствии с принципом Ле Шателье, равновесие ZnS¯ « Zn2+ + S2–
сместится влево, т. е. выпадет дополнительное количество осадка ZnS, и по достижении [Zn2+]×[S2–] = ПР установится новое равновесие.
Какими при этом будут [Zn2+] и [S2–]? Очевидно, что, во-первых, теперь они будут неравными, [S2–] > [Zn2+]. Во-вторых, уменьшением концентрации S2– по сравнению с добавленной, 0,1 моль/л, можно пренебречь, т. к. даже при 100 % связывании ионов цинка она уменьшится всего на 1,4×10–11 моль/л (такой была первоначальная концентрация сульфид-ионов).
Следовательно, для нового состояния равновесия можно записать:
ПР = [Zn2+]× [S2–] = [Zn2+] × С(Na2S) = 2×10–22; откуда
[Zn2+] = ПР/С(Na2S) = 2×10–22/0,1 = 2×10–21 моль/л, и соотношение концентраций ионов цинка и сульфид-ионов в полученном растворе:
[Zn2+]/[S2–] = 2×10–21/ 10–1 = 2×10–20.
Очевидно, что в новом состоянии равновесия показателем растворимости сульфида цинка может быть концентрация только ионов цинка, но не сульфид-ионов, т. к. последние, в основном, – из Na2S.
Таким образом, в присутствии 0,1 моль/л Na2S растворимость ZnS составит 2×10–21 моль/л, и по сравнению с первоначальной уменьшится на 10 порядков (в 10 млрд. раз).
Пример 4. Смешали 0,3 литра раствора хлорида цинка и 1 литр фосфата натрия с начальными концентрациями С(ZnCl2) = 0,1 M и С(Na3PO4) = 1 M. Какая масса фосфата цинка выпадет в осадок; и какими будут концентрации ионов цинка и фосфат-ионов после выпадения осадка и установления равновесия?
Решение
а) напишем уравнения реакции:
3ZnCl2+ 2Na3PO4 ® Zn3(PO4)2¯ + 6NaCl – молекулярное уравнение;
3Zn2+ + 2PO43– ® Zn3(PO4)2¯ – ионно-молекулярное уравнение.
б) определим количество хлорида цинка и фосфата натрия в исходных растворах:
n(ZnCl2) = С(ZnCl2)×Vр-ра = 0,1×0,3 = 0,03 моль,
n(Na3PO4) = С(Na3PO4) ×Vр-ра = 1×1 = 1 моль;
т. о., фосфат натрия – в избытке.
в) рассчитаем количество и массу образующегося осадка Zn3(PO4)2 (по количеству хлорида цинка): из n(ZnCl2) = 0,03 моль получим 0,03/3 = 0,01 моль Zn3(PO4)2 или 3,85 г.
г) определим соотношение молярных концентраций ионов цинка и фосфат-ионов в растворе после выпадения осадка:
После смешивания объем полученного раствора будет равен 1,3 литра. Количество фосфат-ионов в полученном растворе будет равно разнице между первоначальным количеством и прореагировавшим (растворимостью Zn3(PO4)2 можно пренебречь), т. е. n(PO43–) = 1 – 0,02 = 0,98 моль, и их молярная концентрация составит С(PO43–) = 0,98/1,3 = 0,75 моль/л.
Концентрацию ионов цинка рассчитаем из ПР Zn3(PO4)2:
Zn3(PO4)2¯ «3Zn2+ + 2PO43–, ПР = [Zn2+]3× [PO43–]2.
[Zn2+] = 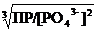 =
= 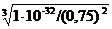 = 1,8×10–11 моль/л.
= 1,8×10–11 моль/л.
Т. о., в результате выпадения осадка соотношение концентраций ионов Zn2+ и PO43– изменилось от 3:100 в момент сливания растворов до 4:1011.
