Теория электродных потенциалов; уравнение Нернста

Равновесный электродный потенциал характеризует равновесие типа Meⁿ⁺ + ne^– ⇆ Me, которое возникает при контакте металла с раствором его соли, и, таким образом, является характеристикой равновесной системы. Поэтому более корректно говорить не о потенциале металла, а о потенциале окислительно-восстановительной системы или о потенциале электродного процесса, например, процесса Cu²⁺ + 2e^– ⇆ Cu.

В общем случае для электродного потенциала системы Ox + ne^– ⇆ Red (где Ox – окисленная форма, т.е. вещество, принимающее электроны, а Red – восстановленная форма, в которую превращается окисленная форма после присоединения электронов), принято следующее обозначение: 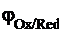. Например, потенциал системы Cu²⁺ + 2e^– ⇆ Cu обозначается .

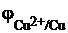Обозначение потенциалаокислительно-восстановительной системы, как и численное значение потенциала не зависит от того, как записано равновесие: и для записи Zn²⁺ + 2e^– ⇆ Zn, и для записи Zn ⇆ Zn²⁺ + 2e^– обозначение потенциала одно и то же: 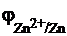, поскольку обе эти записи выражают одно и то же состояние равновесия.

Численное значение электродного потенциала зависит от концентрации веществ в растворе, температуры раствора, а если в процессе участвует газообразное вещество, то и давления. Поэтому для сопоставления электродных потенциалов различных процессов, величины потенциалов обычно приводят к стандартным условиям: концентрация участников реакции в растворе – 1 моль/л, температура – 25°C (298 K), давление – 1 атмосфера. Электродные потенциалы, характеризующие окислительно-восстановительную систему в стандартных условиях, называются стандартными электродными потенциалами и обозначаются j°, например, .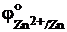

Измерение абсолютного значения потенциала, возникающего на границе металл-раствор не представляется возможным. Поэтому для построения численной шкалы электродных потенциалов нужно потенциал какого-нибудь электрода (точнее говоря, электродного процесса) принять равным нулю и относительно него измерять потенциалы других электродов. В качестве такого эталона принят водородный электрод. Водородный электрод представляет собой пластинку из губчатой платины, которая находится в растворе кислоты (например, HCl или H₂SO₄) и омывается газообразным водородом. Водород хорошо растворяется в платине, при этом молекулы водорода частично распадаются на атомы (платина катализирует этот распад). На поверхности соприкосновения платины с раствором кислоты может протекать окисление атомов водорода или восстановление ионов водорода. Платина при этом не принимает участия в электродных реакциях и играет роль губки, пропитанной водородом. Таким образом, на поверхности водородного электрода протекает процесс 2H⁺ + 2e^– ⇆ H₂. Стандартный электродный потенциал этой системы 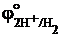и принят равным нулю.

Для того, чтобы определить стандартный электродный потенциал какого-нибудь металла, например, цинка, относительно водородного электрода, необходимо в стандартных условиях собрать гальванический элемент, в котором один электрод будет металлическим (цинковым), а другой – водородным

Zn ÷ ZnCl₂ ÷÷ HCl ÷ H₂ (Pt)

и измерить ЭДС этого элемента:

.

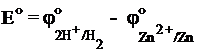Так как .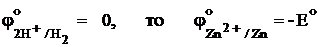

Численное значение электродного потенциала системы a Ox + ne^– ⇆ b Red в нестандартных условиях рассчитывается по уравнению Нернста:

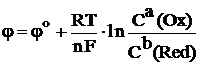(9.2а)

или

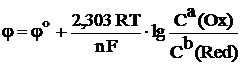, (9.2б)

где j – электродный потенциал в нестандартных условиях (В);

j° – стандартный электродный потенциал (В);

R – универсальная газовая постоянная (8,314 Дж/моль·K);

T – температура (K);

n – число электронов, участвующих в электродном процессе;

F – число Фарадея (96 500 Кулон/моль);

С(Ox) – концентрация окисленной формы (моль/л);

С(Red) – концентрация восстановленной формы (моль/л);

a, b – стехиометрические коэффициенты в уравнении полуреакции.

При постоянной температуре T = 298 K выражение 2,303RT/F представляет собой постоянную величину равную 0,059 . Поэтому для этих условий уравнение Нернста можно записать в другом виде, более удобном для практического применения: 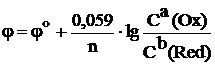. (9.3)

Уравнение Нернста для металлического электрода, находящегося в равновесии с раствором соли этого металла Meⁿ⁺_{(раствор)} + ne^– ⇆ Me (такие электроды называют также электродами первого рода) имеет вид

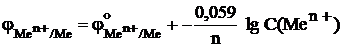. (9.4)

Потенциал водородного электрода 2H⁺ + 2e^– ⇆ H₂ в условиях, отличающихся от стандартных, также можно рассчитать по уравнению Нернста

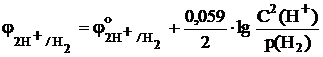, (9.5а)

где p(H₂) – давление газообразного водорода.

При нормальном атмосферном давлении p(H₂) = 1 атм это уравнение преобразуется к виду: 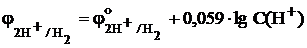. (9.5б)

Учитывая, что 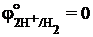, 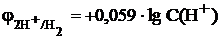; (9.5в)

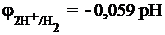. (9.5г)

Пример 9.1 Рассчитать потенциал медного электрода в 0,01 М растворе сульфата меди.

Согласно уравнению Нернста для металлического электрода 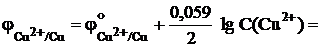+ 0,337 - 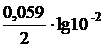= 0,278 В.

Пример 9.2 Рассчитать потенциал водородного электрода при pH=7.

Согласно уравнению Нернста потенциал водородного электрода

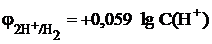= -0,059 pH = -0,059×7 = -0,41 (В).

Пример 9.3 Рассчитать ЭДС гальванического элемента Даниэля-Якоби в стандартных условиях.

Поскольку условия стандартные, то E° = j°_катода - j°_анода =

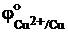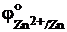= - = +0,337 В - (-0,763 В) = 1,1 В.