Общий анализ однокомпонентных систем. Диаграмма состояния воды. Физический смысл диаграммы состояния воды.

Общий анализ
1. а) Обратимся вначале к наиболее простым – однокомпонентным –системам. Как следует из названия, они содержат лишь одно вещество, которое, однако, может находиться в разных агрегатных состояниях.
б) Итак, здесь К = 1. И положим п = 2, т. е. то, что из внешних параметров на
систему влияют только температура и давление. Тогда правило фаз принимает
вид:
C = 3 – Ф . (7.1)
2. а) Отсюда следует: если в подобной системе — только 1 фаза (Ф = 1), то С = 2 — система имеет 2 степени свободы и называется бивариантной. Это значит,
что в некоторых пределах можно произвольно менять 2 параметра — и дав-
ление, и температуру, — сохраняя то же фазовое состояние. (Об изменении
концентрации говорить не приходится, так как в однокомпонентной системе
вещество находится в чистом виде.)
б) Однако при некоторых значениях Т и Р в системе могут образовываться сразу две фазы (Ф = 2). Тогда С = 1, т. е. система становится моновариантной.
В этом случае для сохранения фазового равновесия произвольно можно
менять либо только Т, либо только Р, а второй параметр должен принимать
некоторое зависимое значение.
в) Наконец, имеется определенная комбинация значений Т и Р, при которой
одновременно сосуществуют сразу три фазы (Ф = 3). Тогда С = 0. Система
становится инвариантной. Изменение любого параметра выводит систему из такого состояния.
3. а) Из выражения (7.1) следует и такой вывод: поскольку С не может быть отрицательным, то в однокомпонентной системе не может одновременно присутствовать больше трех фаз.
б) Для воды, где при умеренных давлениях известны только три агрегатных состояния, это кажется очевидным, хотя при высоких давлениях образуется несколько разных модификаций льда.
в) Или, например, сера имеет 4 агрегатных состояния — две модифика-
ции твердого состояния, а также жидкое и газообразное. И в этом случае
одновременно больше трех состояний существовать не может ни при каких
комбинациях давления и температуры.
7.2. Диаграмма состояния воды: общее описание
Представим на примере воды перечисленные в п. 7.1 ситуации.
1. а) Так, если в однокомпонентной системе — только одна фаза (Ф = 1), то, согласно правилу фаз (7.1), система является бивариантной. В некоторых пределах можно менять сразу и давление, и температуру, и система будет по-прежнему состоять только из этой одной фазы.
б) Но как представить воду, находящуюся только в жидком состоянии? Ведь известно, что над поверхностью воды в реальных условиях всегда есть пар, т. е. вторая (газовая) фаза.
в) Так вот, все, что говорится о состоянии воды с точки зрения правила фаз, наглядней относить к системе под поршнем (рис. 7.1). Поршень создает некоторое давление Р — то внешнее давление, под которым находится система. Изменение этого давления и температуры дает возможность получать различные состояния системы — от однофазного до трехфазного — и построить диаграмму состояния.
г) Обычно построение производят в координатах давление-
температура. Комбинация каких-либо значений Р и Т дает на диаграмме
фигуративную точку, которой соответствует то или иное состояние системы.
2. Для воды подобная диаграмма приведена на рис. 7.2.
а) Ключевое значение имеют три линии, разделяющие диаграмму на три области. Каждая из областей означает, что вода находится только в одном состоянии — жидком (Ж), твердом (Тв) или газообразном (Г).
б) Линии, разделяющие области, — это двухфазные состояния системы, т.е. при значениях Т и Р, отвечающих этим линиям, под поршнем существуют две фазы — именно те, области которых разделены соответствующей линией. Например, линия ОС разделяет области Ж и Г. Соответственно, на данной линии имеются сразу жидкая и газообразная фазы.
в) А точка пересечения всех трех линий, т. е. точка, где сходятся друг с другом все три области, называется тройной. При той паре значений Т и Р, которые соответствуют этой точке, под поршнем присутствуют сразу три фазы — Ж, Тв и Г.
3. Такая диаграмма проясняет смысл результатов, вытекающих из правила
фаз.
а) В пределах каждой области (где Ф = 1) можно менять одновременно оба параметра (и Т, и Р) — и мы будем оставаться внутри данной области, т. е. число и характер фаз будут неизменными.
Это и означает, что если Ф = 1, то С = 2 (система бивариантна).
б) На любой из разделительных линий (где Ф = 2) величины Т и Р уже связаны друг с другом. Чтобы оставаться на линии, относительно произвольно мы можем менять только один параметр, а второй должен изменяться зависимым образом. Это иллюстрация того, что если Ф = 2, то С = 1.
в) И, наконец, сам термин «тройная точка» (где Ф = 3) означает, что нельзя изменить ни одного параметра, чтобы не выйти из этой точки (из трехфазного состояния системы). Степень свободы системы равна нулю. То есть, если Ф = 3, то С = 0 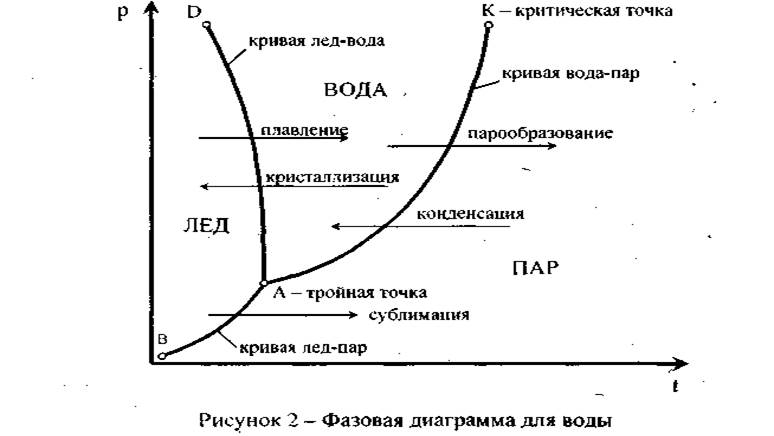Диаграммой фазового равновесия или диаграммой состояния, или фазовой диаграммой называется геометрическое изображение равновесных состояний термодинамической системы при различных значениях параметров состояний. Каждая точка на диаграмме состояния, именуемая фигуративной точкой, определяет численные значения параметров, характеризующих данное состояние системы. С помощью диаграмм состояний можно оценить, сколько фаз и какие конкретно фазы образуют систему при данных значениях параметров состояния. Для однокомпонентных систем используют диаграммы состояния, показывающие зависимость между температурой и давлением. Можно представить существование трех двухфазных и одного трехфазного равновесия для однокомпонентной системы: Л ↔ В ↔ П. Рассмотрим диаграмму состояния однокомпонентной системы (воды), где имеют место - три двухфазных и одно- трехфазное равновесие (рис. 4.1.).Линии, отделяющие одну фазовую область от другой называются линиями фазовых равновесий. В данном случае кривые aa₁, aa₂ и аа₃ делят диаграмму состояния на три поля: лед, вода и пар. Все фигуративные точки, принадлежащие одному полю, отвечают однофазному состоянию и имеют, согласно правилу фаз, две степени свободы: с=1-1+2=2. С = К – Ф + 2,

К – число компонентов = 1 однокомпонентная с-ма, Ф – число фаз, 2 – параметры.

Это означает, что в пределах данного фазового поля одновременное изменение двух параметров состояния не вызывает нарушения фазового равновесия. Линия аа₁ характеризует равновесие Л ↔ П и называется кривой возгонки или сублимации. Она показывает влияние внешнего давления на температуру возгонки вещества. Вместе с тем она характеризует температурную зависимость давления насыщенного пара над твердым веществом. Линия аа₂ соответствует двухфазному равновесию между водой и льдом. Ее называют кривой плавления, т.к. она изображает зависимость температуры плавления от внешнего давления. Линия аа₃ соответствует двухфазному равновесию между водой и паром, характеризующийся одной степенью свободы. Это означает, что можно произвольно изменять только один из параметров состояния - р или Т. Из диаграммы также следует, что линия аа₃ характеризует зависимость давления насыщенного пара данного вещества от температуры и ее можно трактовать как зависимость температуры кипения вещества от внешнего давления. В этой связи кривая аа₃ получила название кривой кипения или кривой испарения.

На линиях может изменяться только один параметр, Т или р. с = 1- 2 + 2 = 1 Линии равновесия аа₃ , aa₁ и аа₂ сходятся в тройной точке а, где сосуществуют все три фазы. Согласно правилу фаз для трехфазного равновесия в однокомпонентной системе число степеней свободы равно 0. Это означает, что три фазы могут находиться в равновесии друг с другом сколь угодно долго, но при строго определенных значениях параметров состояния. с = 1 – 3 + 2 = 0.