Тема 3. Химическая термодинамика
Литература: [1] c.116-148; [2] с.166-169, 195-204; [3] c.159-175
Теоретические основы
Химическая термодинамика изучает изменения в состоянии веществ при физико-химических превращениях, выясняет возможность и степень самопроизвольного протекания химических реакций.
Внутреннее состояние веществ в химической термодинамике характеризуется такими важнейшими термодинамическими функциями состояния, как энтальпия (Н), энтропия (S) и свободная энергия Гиббса, или изобарно-изотермический потенциал (G).
Энтальпия определяется содержанием в веществах внутренней энергии. Изменение энтальпии в ходе химической реакции (DН) сопровождается тепловым эффектом (Q), который может быть экспериментально измерен. При условии постоянства давления (изобарный процесс) DН и Q равны по абсолютной величине и противоположны по знаку. Если теплота выделяется, реакция называется экзотермической. При этом DН<0 и Q>0. Для эндотермической реакции (протекает с поглощением теплоты) справедливы неравенства: DН>0 и Q<0. Тепловой эффект реакции образования одного моля вещества из простых веществ носит название теплоты образования.
Энтропия характеризует неупорядоченность внутреннего состояния вещества. С увеличением хаотичности в расположении и движении частиц, составляющих данное вещество, её значение возрастает. Так, энтропия увеличивается при повышении температуры, плавлении и испарении вещества (переходы от кристаллического состояния к менее упорядоченному жидкому и далее к газообразному) и, особенно, при сублимации (испарение твёрдого тела). Энтропия изменяется и в ходе химической реакции. При этом знак величины DS (р-ции) свидетельствует о характере изменения беспорядка в расположении и перемещении атомов и молекул.
В химических процессах одновременно проявляются две тенденции: стремление частиц объёдиняться в более сложные, т.е. к большему порядку в их расположении, что уменьшает энтальпию, и стремление частиц разъёдиниться, т.е. к большей хаотичности, что увеличивает энтропию. Суммарный эффект этих двух противоположных тенденций в процессах, протекающих при постоянных температуре и давлении, отражается в характере изменения свободной энергии Гиббса (изобарно-изотермический потенциал):
DG = DH - TDS,
где энтальпийный (DH) и энтропийный (ТDS) факторы выражены в одинаковых единицах измерения - кДж/моль.
По знаку величины DG в ходе химической реакции можно сделать вывод о принципиальной возможности самопроизвольного протекания этой реакции при стандартных условиях: DG < 0 - процесс принципиально осуществим;
DG > 0 - процесс самопроизвольно протекать не может;
DG = 0 - система находится в состоянии равновесия.
Термодинамические функции состояния обладают общим свойством: их изменение в ходе химической реакции не зависит от пути этой реакции, а определяется только природой конечных и начальных веществ. Например, для реакции:
аА + bB = cC + dD
значения DH(р-ции), DS(р-ции), DG(р-ции) можно вычислить как разность между суммой стандартных значений соответствующих функций (DH°298 - стандартных теплот образования, DS°298 - стандартных энтропий, DG°298 - свободных энергий Гиббса образования) для продуктов реакции и суммой значений тех же функций для исходных веществ:
DH(р-ции) = [c·DH°298(C) + d·DH°298(D)] - [a·DH°298(A) +
+ b·DH°298(B)];
DS(р-ции) = [c·S°298(C) + d·S°298(D)] - [a·S°298(A) +
+ b·S°298(B)];
DG(р-ции) = [c·DG°298(C) + d·DG°298(D)] - [a·DG°298(A) +
+ b·DG°298(B)];
Значения теплот образования и стандартных энтропий приведены в приложении 2. Стандартное изменение свободной энергии Гиббса в химической реакции можно рассчитать также по формуле:
DG(р-ции) = DH(р-ции) - Т·DS(р-ции) (Т = 298 К).
DH(р-ции) и DS(р-ции) мало зависит от температуры. Поэтому из условия принципиальной осуществимости реакции
DH(р-ции) - Т·DS(р-ции) < 0 или Т·DS(р-ции) > DH(р-ции)
можно примерно определить температуру, выше или ниже которой происходит данная реакция.
В качестве примера произведём термодинамический расчёт двух химических реакций.
I. 2 Сu(NO3) 2 (т) ¾® 2СuO(т) + 4NO2(г) + O2(г)
Изменение энтальпии при стандартных условиях:
DH(р-ции) = [2·DH°298(CuO) + 4·DH°298(NO2)] -
-[2·DH°298(Сu(NO3)2] = 2·(-182.1) + 4·(33.5) - 2·(-305.3) =
= 420.4 кДж.
Изменение энтропии при стандартных условиях: DS(р-ции) = [2·S°298(CuO) + 4·S°298(NO2) + S°298(O2)] -
-[2·S°298(Сu(NO3)2] = 2·42.7 + 4·240.3 + 205.0 - 2·109.0 =
= 1033.6 Дж/K = 1.034 кДж/К.
Изменение свободной энергии Гиббса при стандартных условиях:
DG(р-ции) = 420.4 - 298·1.034 = 112.3 кДж.
Выводы:
1. Положительный знак DH(р-ции) говорит о том, что реакция протекает с поглощением теплоты (Q(р-ции) < 0), т.е. является эндотермической. Это энтальпийно невыгодный процесс.
2. Характер изменения энтропии (DS(р-ции) > 0) свидетельствует об увеличении беспорядка в расположении и перемещении частиц. Большое положительное значение DS(р-ции) обусловлено резким возрастанием объёма системы (объём газообразных продуктов намного больше объёма твердого исходного вещества). Это энтропийно выгодный процесс.
3. Положительный знак DG(р-ции) указывает на невозможность самопроизвольного протекания данной реакции при стандартных условиях. Вычислим температуру, выше которой начинается эта реакция: Т > DH/DS = 420.4/1.034= = 407 К, или реакция возможна при t > 134°C.
II.CO(г) + Cl2(г) ¾® COCl2(г)
Изменение энтальпии при стандартных условиях: DH(р-ции) = DH°298(COСl2) - DH°298(СO) = -220.3 - (-110.6) = = - 109.7 кДж.
Изменение энтропии при стандартных условиях: DS(р-ции) = S°298(COСl2) - [S°298(СO) + S°298(Сl2)] = 283.9- - (197.7 + 222.9) = - 136.7 Дж/K = - 0.137 кДж/K.
Изменение свободной энергии Гиббса при стандартных условиях: DG(р-ции) = -109.7 - 298·(-0.137) = - 68.9 кДж.
Выводы:
1. Отрицательный знак DH(р-ции) говорит о том, что реакция протекает с выделением теплоты (Q(р-ции) >0), т.е. является экзотермической. Это энтальпийно выгодная реакция.
2. Характер изменения энтропии (DS(р-ции) < 0) свидетельствует об увеличении порядка в расположении и перемещении частиц. Отрицательное значение DS(р-ции) обусловлено уменьшением объёма системы (из двух молей газообразных веществ образуется один). Это энтропийно выгодный процесс.
3.Отрицательный знак DG(р-ции) указывает на возможность самопроизвольного протекания данной реакции при стандартных условиях. Вычислим температуру, выше которой эта реакция самопроизвольно не протекает:
Т·DS(р-ции) > DH(р-ции) ; - 0.137·Т > - 109.7, или
0.137Т < 109.7, откуда Т < 109.7/0.137 = 801 K, или реакция возможна при температуре t < 528° C.
Задачи 41 - 60
Используя данные приложения 2, вычислить стандартные изменения энтальпии (DH), энтропии (DS) и свободной энергии Гиббса (DG) для химических реакций, уравнения которых указаны ниже. Объясните характер изменения энтальпии (экзо- или эндотермическая реакция; выделяется или поглощается теплота) и энтропии (DS > 0, DS < 0, DS = 0). Возможна ли данная реакция при стандартных условиях ? При какой температуре она начинается?
У р а в н е н и я р е а к ц и й
41. C3H6(г) + Н2(г) = C3Н8(г)
42. Fe3O4(т) + CO(г) = 3FeO(т) + CO2(г)
43. Cu2S(т) + 2O2(г) = 2CuO(т) + SO2(г)
44. C2H5OH(ж) + 3O2(г) = 2CO2(г) + 3H2O(г)
45. C2H4(г) + 3O2(г) = 2CO2(г) + 2H2O(ж)
46. CО(г) + 3Н2(г) = CН4(г) + H2O(г)
47. 2CO(г) + O2(г) = 2CO2(г)
48. Fe2O3(т) + 3H2(г) = 2Fe(т) + 3H2O(г)
49. 4НJ(г) + О2(г) = 2J2(г) + 2Н2O(г)
50. Fe2O3(т) + 3СО(г) = 2Fe(т) + 3СО2(г)
51. N2(г) + 3H2(г) = 2NH3(г)
52. С2Н2(г) + 2H2(г) = С2Н6(г)
53. 4NH3(г) + 5O2(г) = 4NO(г) + 6H2O(г)
54. H2(г) + СО2(г) = СО(г) + H2O(ж)
55. 3N2O(г) + 2NH3(г) = 4N2(г) + 3H2O(г)
56. 4NH3(г) + 3O2(г) = 2N2(г) + 6H2O(г)
57. CO2(г) + Н2(г) = CO(г) + Н2O(ж)
58. 2H2S(г) + 3O2(г) = 2SO2(г) + 2Н2O(ж)
59. 2H2S(г) + O2(г) = 2S(т) + 2Н2O(г)
60. РН3(г) + 2О2(г) = Н3РО4(т)
Тема 4. Химическая кинетика
И равновесие
Литература: [1] c.143-151, 167-189; [2] с.170-195; [3] c.176-206
Теоретические основы
Скорость химической реакции представляет собой число элементарных актов этой реакции в единицу времени в единице объёма для гомогенных реакций или на единице площади поверхности раздела фаз для гетерогенных реакций.
Из множества молекул при столкновении химически взаимодействуют только те, энергия которых не ниже энергии активации. Доля таких молекул, они называются активными, а также величина энергии активации (высота активационного барьера) определяют величину скорости химической реакции.
На практике это проявляется в зависимости скорости реакции от природы и концентрации реагирующих веществ, температуры, природы реакционной среды (например, природы растворителя) и присутствия катализаторов. Каждый из указанных факторов так или иначе влияет либо на долю активных молекул, либо на высоту активационного барьера.
Зависимость скорости реакции от температуры выражается формулой Вант-Гоффа 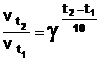 , где
, где 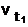 - скорость реакции при температуре t1 ,
- скорость реакции при температуре t1 , 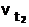 - скорость реакции при температуре t2 , g - температурный коэффициент реакции. Например, при повышении температуры от 20° до 60° скорость реакции, температурный коэффициент которой равен 3, возрастает в
- скорость реакции при температуре t2 , g - температурный коэффициент реакции. Например, при повышении температуры от 20° до 60° скорость реакции, температурный коэффициент которой равен 3, возрастает в 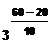 = 34 = 81 раз.
= 34 = 81 раз.
Согласно закону действия масс изменение концентрации реагирующих веществ вызывает пропорциональное изменение скорости реакции. Так, для реакции
аА + вВ ¾® сС + dD
скорость будет пропорциональна произведению концентрации веществ А и В, взятых в степенях, соответствующих стехиометрическим коэффициентам при формулах этих веществ в уравнении реакции: 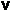 = k [A]a•[B] b.
= k [A]a•[B] b.
При этом концентрации твёрдых веществ считаются практически неизменными и в явном виде не включаются в выражение для скорости. Например, скорость реакции железа с соляной кислотой
Fe (тв) + 2HCl (р-р) = FeCl2 (р-р) + H2 (г)
выражается только черезконцентрацию кислоты:
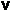 = k [HCl]2.
= k [HCl]2.
При увеличении концентрации HCl, например, в 3 раза, скорость этой реакции возрастает в 32 раза, т.е. в 9 раз.
Для газообразных веществ изменения концентраций можно достичь, изменяя внешнее давление в реакционной системе. Например, при повышении давления в 4 раза в системе 2SO2 (г) + O2 (г) = 2SO3 (г) (*)
скорость этой реакции 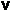 = k [SO2]2•[O2] возрастёт в 42• 4 = 64 раза, так как при этом так же в четыре раза увеличится концентрация каждого газообразного компонента.
= k [SO2]2•[O2] возрастёт в 42• 4 = 64 раза, так как при этом так же в четыре раза увеличится концентрация каждого газообразного компонента.
Большинство химических реакций является обратимыми: одновременно протекает прямая (слева направо) и обратная (справа налево) реакции. В момент выравнивания скоростей этих реакций в системе наступает химическое равновесие

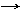 аА + вВ сС + dD,
аА + вВ сС + dD,
характеризуемое константой равновесия:
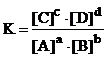 .
.
Например, константа равновесия для реакции (*)
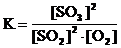 .
.
Следует учесть, что в случае гетерогенных равновесий, например, MgSО3 (тв) = MgО (тв) + SО2 (г) концентрации
твёрдых веществ в явном виде не записывают в выражении для константы химического равновесия: К = [SO2].
Направление смещения равновесия определяется стремлением системы противодействовать вмешательству извне (принцип Ле Шателье).
Так, нагревание смещает равновесие в сторону эндотермической реакции, происходящей с поглощением тепла. Охлаждение - в сторону экзотермической реакции, сопровождающейся выделением тепла.
Повышение давления вызывает смещение равновесия в сторону реакции, протекающей с уменьшением объёма или числа молей газообразных веществ. Напротив, понижение давления - в сторону реакции с увеличением объёма (числа молей газообразных веществ).
Увеличение концентрации исходных веществ сдвигает равновесие вправо, а увеличение концентрации продуктов взаимодействия - влево. В общем случае повышение концентрации какого-либо компонента реакционной системы смещает равновесие в сторону той реакции, в которой этот компонент расходуется.
Например, в системе (*) прямая реакция экзотермична, протекает с уменьшением числа молей газообразных веществ, из трёх молей исходных газов образуются два моля газообразного продукта. Поэтому для смещения равновесия слева направо, в сторону прямой реакции, необходимо понизить температуру по сравнению с равновесной, повысить давление и концентрации SO2 и О2 или понизить концентрацию SO3 (отводить его из сферы реакции по мере образования).
Задачи 61 - 80
Составьте выражения для скоростей прямой, обратной реакций (уравнение реакции то же, что в предыдущей задаче), константы равновесия. Вычислите, во сколько раз изменится скорость прямой реакции при заданном изменении температуры, концентрации и давлении (табл. 4). Как необходимо изменить внешние условия (температуру, давление, концентрации веществ) для смещения равновесия слева направо?
Т а б л и ц а 4
| Номер задачи | 61 62 63 64 65 66 67 68 69 70 |
| Уравнение в задании темы 3 | 41 42 43 44 45 46 47 48 49 50 |
          Темп.коэф-иент t1 t2 n1 (концентрация 1-ого компонента увеличилась в n1 раз) n2 (концентрация 2-ого компонента увеличилась в n2 раз) m (давление уве- личилось в m раз) Темп.коэф-иент t1 t2 n1 (концентрация 1-ого компонента увеличилась в n1 раз) n2 (концентрация 2-ого компонента увеличилась в n2 раз) m (давление уве- личилось в m раз) | 2 3 3 2 2 3 2 2 4 2 110 90 100 20 30 40 80 130 90 90 120 110 130 50 70 90 70 140 100 100 3 3 4 5 6 7 2 4 8 3 8 8 4 5 1 100 1 5 6 15 2 3 2 10 2 3 2 3 2 10 |
продолжение таблицы
| Номер задачи | 71 72 73 74 75 76 77 78 79 80 |
| Уравнение в задании темы 3 | 51 52 53 54 55 56 57 58 59 60 |
          Температурный коэффициент t1 t2 n1 (концентрация 1-ого компонента увеличилась в n1 раз) n2 (концентрация 2-ого компонента увеличилась в n2 раз) m (давление уве- личилось в m раз) Температурный коэффициент t1 t2 n1 (концентрация 1-ого компонента увеличилась в n1 раз) n2 (концентрация 2-ого компонента увеличилась в n2 раз) m (давление уве- личилось в m раз) | 2 3 4 4 2 3 4 2 2 2 50 90 10 30 30 50 60 50 40 20 70 120 30 60 70 100 80 70 50 40 1 3 2 5 2 2 10 4 4 12 10 2 2 3 3 4 3 2 6 5 5 4 2 8 3 3 7 4 5 6 |
Тема 5. Растворы
Литература: [1] c. 204-231; [2] с. 213-230; [3] c.125-134
Теоретические основы
Многие химические реакции протекают в растворах. В истинных растворах растворённое вещество диспергировано до его мельчайших частиц (молекул, ионов или атомов). Истинными растворами называются гомогенные системы переменного состава, состоящие из двух или более компонентов.
Состав раствора выражают концентрацией растворённых веществ. Основными способами выражения концентрации являются:
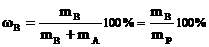 |
1.Массовая доля растворённого вещества (wв) – это количество весовых частей растворённого вещества, содержащегося в ста весовых частях раствора (выражается в %):
где mр – масса раствора (например, в граммах), mА – масса растворителя (г), mв – масса растворенного вещества (г).
2. Молярность, или молярная концентрация (С) – это количество вещества (nв, моль) растворённого вещества, содержащееся в 1 литре раствора (выражается в моль/л º М):
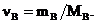
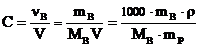 |
где Mв – молярная масса растворённого вещества (г/моль), V – объём раствора в литрах, r - плотность раствора (г/мл), причём количество вещества растворённого вещества:
3. Моляльность, или моляльная концентрация (Сm) – это количество вещества (nв, моль) растворённого вещества, приходящееся на 1 кг растворителя (выражается в моль/кг):
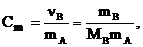
где mА – масса растворителя (кг).
4. Мольная доля растворённого вещества (cв) – это отношение количества вещества растворённого вещества к сумме количества вещества всех веществ в растворе:
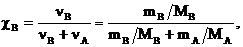
где nА – количество вещества растворителя (моль), MА – молярная масса растворителя (г/моль).
Очень разбавленные растворы (с низкой концентрацией растворенного вещества) по своим свойствам приближаются к идеальным растворам. В идеальных растворах каждый компонент ведёт себя независимо от других компонентов. В таких растворах силы межмолекулярного взаимодействия между компонентами одинаковы. Коллигативные (общие, или коллективные) свойства идеальных растворов зависят от концентрации и практически не зависят от природы растворённых веществ. К ним, в частности, относятся повышение температуры кипения и понижение температуры замерзания растворов и осмотическое давление.
Температура кипения растворов выше температуры кипения растворителей. Согласно закону Рауля повышение температуры кипения DТкип пропорционально моляльности раствора и не зависит от природы растворенного вещества
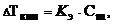
где Кэ - эбулиоскопическая постоянная растворителя.
Температура замерзания (кристаллизации) растворов ниже температуры замерзания (кристаллизации) чистых растворителей. Согласно закону Рауля понижение температуры замерзания DТзам пропорционально моляльности раствора и не зависит от природы растворенного вещества
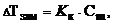
где Кк - криоскопическая постоянная растворителя.
Значения Кэи Кк (измеряются в кг×К/моль) зависят от природы растворителей. Например, для воды: Кэ = 0,52и Кк = 1,86; для этанола: Кэ = 1,22и Кк = 1,99.
Используя уравнения закона Рауля можно определить молярную массу растворенного вещества. Для этого экспериментально находят DТкип и DТзам. Зная массу растворенного вещества mв и растворителя mА, рассчитывают молекулярную массу растворенного вещества Mв по уравнению
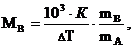
где К º Кэ или К º Кк.
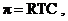 Если раствор и растворитель разделены полупроницаемой мембраной, то возможен самопроизвольный переход молекул растворителя из растворителя в раствор. Односторонняя диффузия частиц через пористую перегородку получила название «осмос». Раствор при этом разбавляется, и высота его столба увеличивается. Количественно осмос характеризуется осмотическим давлением p, которое равно давлению столба раствора в осмометре высотой h. Согласно закону Вант-Гоффа осмотическое давление относительно чистого растворителя пропорционально молярной концентрации раствора где R = 8,314 Дж/К×моль –
Если раствор и растворитель разделены полупроницаемой мембраной, то возможен самопроизвольный переход молекул растворителя из растворителя в раствор. Односторонняя диффузия частиц через пористую перегородку получила название «осмос». Раствор при этом разбавляется, и высота его столба увеличивается. Количественно осмос характеризуется осмотическим давлением p, которое равно давлению столба раствора в осмометре высотой h. Согласно закону Вант-Гоффа осмотическое давление относительно чистого растворителя пропорционально молярной концентрации раствора где R = 8,314 Дж/К×моль –
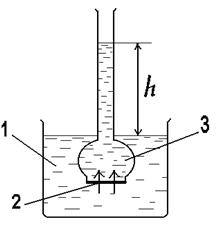
Рис.5. Схема осмометра: 1 - вода; 2 - раствор; 3-полупроницаемая мембрана.
универсальная газовая постоянная, Т – абсолютная температура, С – молярная концентрация раствора.
Осмос играет важную роль в биологических процессах, обеспечивая поступление воды. Растворы сахара (сироп) и соли (рассол) широко применяются для консервирования продуктов, так как вызывают удаление воды из микроорганизмов.
Пример. Приготовлен раствор с плотностью r = 1,01 г/мл из 1,5 г глутаминовой кислоты (Mв = 147 г/моль) и 100 г воды (MА = 18 г/моль). Рассчитать массовую и мольную доли глутаминовой кислоты в растворе, молярную и моляльную концентрации раствора, повышение температуры кипения и понижение температуры замерзания, а также величину осмотического давления, если мембрана пропускает только молекулы воды и температура опыта 25°С. Постоянные воды: Кэ = 0,52и Кк = 1,86.
Массовая доля:
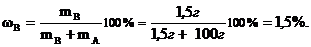
Мольная доля:
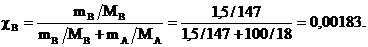
Моляльность:
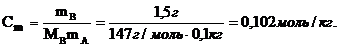
Молярность:
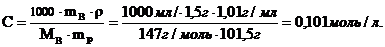
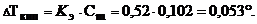 Повышение температуры кипения:
Повышение температуры кипения:
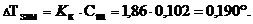 Понижение температуры замерзания:
Понижение температуры замерзания:
Осмотическое давление:
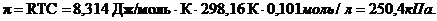
Задачи 81-100
По данным таблицы 4 рассчитайте массовую и мольную доли растворённого в 100 г воды(MА = 18 г/моль) вещества, молярную и моляльную концентрации соответствующего раствора, повышение температуры кипения и понижение температуры замерзания, а также величину осмотического давления, если мембрана пропускает только молекулы воды и температура опыта 25°С. Постоянные воды: Кэ = 0,52и Кк = 1,86.
Таблица 5
| Номер задачи | Растворённое вещество | Плотность раствора, r (г/моль) | ||
| Название | Молярная масса, МВ (г/моль) | Масса на 100 г воды, mВ (г) | ||
| Глицерин | 5,27 | 1,010 | ||
| Глицерин | 7,53 | 1,015 | ||
| Глицерин | 8,70 | 1,018 | ||
| Глицерин | 11,10 | 1,022 | ||
| Уксусн. кислота | 2,04 | 1,001 | ||
| Уксусн. кислота | 3,09 | 1,002 | ||
| Уксусн. кислота | 4,17 | 1,004 | ||
| Уксусн. кислота | 5,26 | 1,005 | ||
| Уксусн. кислота | 6,38 | 1,007 | ||
| Уксусн. кислота | 7,53 | 1,008 | ||
| Фруктоза | 1,85 | 1,020 | ||
| Глюкоза | 3,01 | 1,030 | ||
| Галактоза | 5,04 | 1,050 | ||
| Арабиноза | 2,55 | 1,030 | ||
| Ксилоза | 4,60 | 1,050 | ||
| Рибоза | 6,20 | 1,060 | ||
| Дезоксирибоза | 5,86 | 1,060 | ||
| Сахароза | 8,40 | 1,080 | ||
| Сорбит | 3,64 | 1,040 | ||
| Гулоза | 2,70 | 1,030 |
