Уравнение Клапейрона – Менделеева

Молярная масса газов можно вычислить также, пользуясь уравнением идеального газа – уравнением Клапейрога – Менделеева:

pV = mBRT/MB

где p – давление газа, Па; V – его объем; mB – масса вещества, г; MB – его молярная масса, г/моль; T – абсолютная температура, К; R – универсальная газовая постоянна, равная 8,314 Дж/(моль К).

Если объем и давление газа выражены в других единицах измерения, то значение газовой постоянной в уравнении Клапейрона – Менделеева примет другое значение. Оно может быть рассчитано по формуле, вытекающей из объединенного закона газового состояния для моля вещества при нормальных условиях:

R= (pо Vо/Tо)для одного моля газа

Строение атома. Ранние модели атома. Постулаты Бора.

Атом (от др.-греч. ἄτομος — неделимый) — наименьшая химически неделимая часть химического элемента, являющаяся носителем его свойств^[1]. Атом состоит из атомного ядра и окружающего его электронного облака. Ядро атома состоит из положительно заряженных протонови незаряженных нейтронов, а окружающее его облако состоит из отрицательно заряженных электронов. Если число протонов в ядре совпадает с числом электронов, то атом в целом оказывается электрически нейтральным. В противном случае он обладает некоторым положительным или отрицательным зарядом и называется ионом. Атомы классифицируются по количеству протонов и нейтронов в ядре: количество протонов определяет принадлежность атома некоторому химическому элементу, а число нейтронов — изотопу этого элемента.

Дж. Дж. Томсон (Около 1900 г.) предлагает первую модель атома, согласно которой положительный заряд равномерно заполняет весь объем атома, а отрицательный, представленный электронами, вкраплен в эту положительно заряженную сферу. Эта модель получила название «пудинг Томсона».

Ранняя планетарная модель атома Нагаоки. В 1904 году японский физик Хантаро Нагаока

предложил модель атома, построенную по аналогии с планетой Сатурн. В этой модели вокруг маленького положительного ядра по орбитам вращались электроны, объединённые в кольца. Модель оказалось ошибочной, но некоторые важные её положения вошли в модель Резерфорда.^{[источник не указан 600 дней]}

Планетарная модель атома Бора-Резерфорда. В 1911 году ^[11] Эрнест Резерфорд, проделав ряд экспериментов, пришёл к выводу, что атом представляет собой подобие планетной системы, в которой электроны движутся по орбитам вокруг расположенного в центре атома тяжёлого положительно заряженного ядра («модель атома Резерфорда»). Однако такое описание атома вошло в противоречие с классической электродинамикой. Дело в том, что, согласно классической электродинамике, электрон при движении с центростремительным ускорением должен излучать электромагнитные волны, а, следовательно, терять энергию. Расчёты показывали, что время, за которое электрон в таком атоме упадёт на ядро, совершенно ничтожно. Для объяснения стабильности атомов Нильсу Бору пришлось ввести постулаты, которые сводились к тому, что электрон в атоме, находясь в некоторых специальных энергетических состояниях, не излучает энергию («модель атома Бора-Резерфорда»). Постулаты Бора показали, что для описания атома классическая механика неприменима. Дальнейшее изучение излучения атома привело к созданию квантовой механики, которая позволила объяснить подавляющее большинство наблюдаемых фактов.

Постулаты

Модель атома Бора

· Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам для которых момент импульса квантуется: 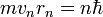, где n - натуральные числа, а 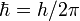- постоянная Планка. Пребывание электрона на орбите определяет энергию этихстационарных состояний

.

· При переходе электрона с орбиты на орбиту излучается или поглощается квант энергии hν = E_n − E_m, где E_n;E_m — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.

Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемуюБоровской моделью атома^[1]. В дальнейшем Зоммерфельд расширил теорию Бора на случай эллиптических орбит. Её называют моделью Бора-Зоммерфельда.

5. Состояние электронов в атоме. Квантовые числа. Геометрическая интерпретация главного, орбитального и магнитного квантовых чисел.

Состояние каждого электрона в атоме обычно описывают с помощью четырех квантовых чисел: главного (n), орбитального (l), магнитного (m) и спинового (s). Первые три характеризуют движение электрона в пространстве, а четвертое - вокруг собственной оси.

Главное квантовое число (n). Определяет энергетический уровень электрона, удаленность уровня от ядра, размер электронного облака. Принимает целые значения (n = 1, 2, 3 ...) и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома и какой энергетический уровень является внешним.

Пример.

Элемент кадмий Cd расположен в пятом периоде, значит n = 5. В его атоме электроны раcпределены по пяти энергетическим уровням (n = 1, n = 2, n = 3, n = 4, n = 5); внешним будет пятый уровень (n = 5).

Орбитальное квантовое число (l) характеризует геометрическую форму орбитали. Принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, cодинаковыми n и l - подуровнем.

Для

l=0 s- подуровень, s- орбиталь – орбиталь сфера

l=1 p- подуровень, p- орбиталь – орбиталь гантель

l=2 d- подуровень, d- орбиталь – орбиталь сложной формы

f-подуровень, f-орбиталь – орбиталь еще более сложной формы

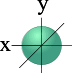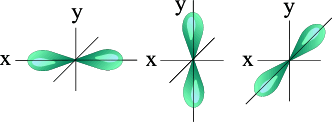S - орбиталь	Три p – орбитали

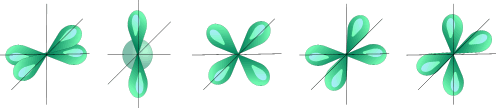Пять d – орбиталей