Зависимость скорости реакции от температуры
Скорость реакции увеличивается с повышением температуры. Это объясняется увеличением скорости движения молекул, что делает столкновения между ними более результативными (ускорение реакции за счет увеличения числа столкновений между молекулами хотя и имеет место, но пренебрежимо мало по сравнению с фактором возрастания энергии столкновений).
Опытным путем голландский ученый Якоб Вант-Гофф установил правило, выражающее зависимость скорости реакции от температуры и названное его именем.
Правило Вант-Гоффаформулируется следующим образом:
При повышении температуры на каждые 10 градусов скорость реакции увеличивается в 2—4 раза.
Это означает, что при повышении температуры в арифметической прогрессии скорость химической реакции возрастает в геометрической прогрессии.
Основанием в формуле прогрессии является температурный коэффициент скорости реакции γ, показывающий, во сколько раз увеличивается скорость (или, что то же самое — константа скорости) данной реакции при росте температуры на 10 градусов. Математически правило Вант-Гоффа выражается формулами:
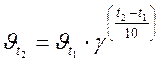 или
или 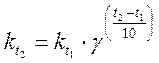
где 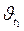 и
и 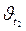 – скорости реакции соответственно при начальной t1 и конечной t2 температурах.
– скорости реакции соответственно при начальной t1 и конечной t2 температурах.
Правило Вант-Гоффа может быть также выражено следующими соотношениями:
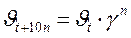 ;
; 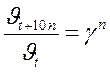 ;
; 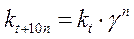 ;
; 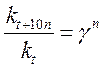 ,
,
где 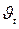 и
и 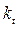 – соответственно скорость и константа скорости реакции при температуре t ;
– соответственно скорость и константа скорости реакции при температуре t ; 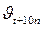 и
и 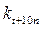 – те же величины при температуре t +10n; n – число «десятиградусных» интервалов (n =(t2–t1)/10), которые составляют интервал повышения температуры t2–t1.
– те же величины при температуре t +10n; n – число «десятиградусных» интервалов (n =(t2–t1)/10), которые составляют интервал повышения температуры t2–t1.
Величина n может быть целым числом, если интервал повышения температуры t2–t1 кратен десяти, но в общем случае является дробным. При целочисленном значении n при расчете температурного коэффициента можно находить корень n-ой степени из отношения скоростей реакции. В общем случае, по логарифму отношения скоростей реакции находят значение логарифма температурного коэффициента, а затем вычисляют антилогарифм (величину 10x). Если позволяют возможности калькулятора, при дробном значении n можно непосредственно вычислять корень n-ой степени, где n — нецелое число, из отношения скоростей реакции
Более точно, чем по правилу Вант-Гоффа, зависимость константы скорости от температуры описывается уравнением Аррениуса
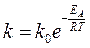 , (4)
, (4)
где е – основание натуральных логарифмов, ЕА – энергия активации, Т – абсолютная температура, R – универсальная газовая постоянная; k0 – предэкспоненциальный множитель (константа, зависящая от природы реагирующих веществ).
Для прохождения химической реакции между частицами (атомами, молекулами, ионами) необходимо их столкновение. Но к взаимодействию, то есть к химической реакции, приводит не каждое столкновение; взаимодействие возможно лишь в случае, когда энергия частиц достаточно велика, чтобы они сблизились на такое расстояние, при котором произошло бы перекрывание их электронных облаков и последующее перераспределение электронной плотности. При этом одни связи разрушаются, а другие образуются. Согласно теории активации в химическое взаимодействие вступают только активные молекулы, т.е. имеющие избыточное количество энергии по сравнению со средней величиной.
Энергией активацииданной реакции называется энергия, которую необходимо сообщить одному молю реагирующего вещества, чтобы все молекулы стали активными. Энергия активации ЕА выражается в кДж/моль, и чем больше ее значение, тем больше изменение температуры влияет на скорость данной реакции; соответственно, тем больше значение температурногокоэффициента скорости реакции γ в формуле Вант-Гоффа.
Уравнение Аррениуса (4) часто используют в логарифмической форме
записи:
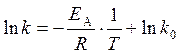 ,
,
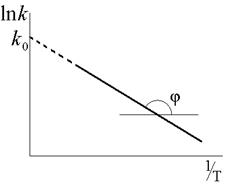 |
| Рис 2. Зависимость константы скорости реакции от температуры |
из которой следует, что зависимость константы скорости реакции, построенная в координатах lnk — 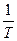 , является линейной (рис. 2). Таким образом, если определить две константы скорости данной реакции k1 и k2 при температурах Т1 и Т2 , то можно также определить энергию активации реакции по тангенсу угла наклона прямой tgφ = EA/R , поскольку отношение EA/R выполняет роль коэффициента перед переменной в уравнении прямой линии. При этом нет необходимости выяснять значение предэкспоненциального множителя k0 , (его обычно определяют экстраполяцией зависимости на ось ординат), и энергию активации вычисляют по формуле:
, является линейной (рис. 2). Таким образом, если определить две константы скорости данной реакции k1 и k2 при температурах Т1 и Т2 , то можно также определить энергию активации реакции по тангенсу угла наклона прямой tgφ = EA/R , поскольку отношение EA/R выполняет роль коэффициента перед переменной в уравнении прямой линии. При этом нет необходимости выяснять значение предэкспоненциального множителя k0 , (его обычно определяют экстраполяцией зависимости на ось ординат), и энергию активации вычисляют по формуле:
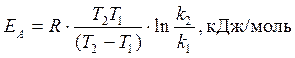 .
.
Примеры решения задач
Пример 1. Написать выражения закона действия масс для следующих реакций:
а) 2NO(газ) + Сl2 (газ) = 2NOCl(газ) ;
б) CaCO3 (тверд.) = CaO (тверд.) + CO2 (газ) .
Решение.
а) Оба исходных реагента – газы, поэтому их концентрации войдут в выражение для скорости реакции в соответствии с формулировкой закона действия масс:
υ = k·[NO]2·[Cl2].
б) Карбонат кальция – твердое вещество, концентрация которого не изменяется в ходе реакции, поэтому его концентрация в выражение закона действия масс не входит, а других исходных реагентов в данной реакции нет. Следовательно, выражение для скорости будет иметь вид:
υ = k ,
и в данном случае скорость реакции (при постоянной температуре) будет постоянной величиной.
Пример 2. Как изменится скорость реакции 2СO + О2 = 2СО2 , протекающей в закрытом сосуде, если увеличить давление в 2 раза?
Решение. Скорость указанной химической реакции определяется выражением:
υнач = k·[СО]2·[О2].
Увеличение давления приводит к увеличению концентрации обоих реагентов в 2 раза. С учетом этого перепишем выражение закона действующих масс:
υ1 = k·[2СО]2·[2О2] = k·22[СО]2·2[О2] = 8k·[СО]2·[О2] = 8 υнач .
Ответ: Скорость реакции увеличится в 8 раз.
Пример 3.Вычислить, во сколько раз увеличится скорость реакции, если повысить температуру системы от 20 °С до 100 °С,
приняв значение температурного коэффициента скорости реакции равным 3.
Решение. Отношение скоростей реакции при двух разных температурах связано с температурным коэффициентом и изменением температуры формулой:
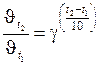 .
.
Вычисление:
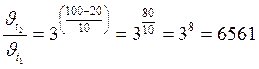 .
.
Ответ: Скорость реакции увеличится в 6561 раз.
Пример 4. .При изучении гомогенной реакции А + 2В = 3D установлено, что в течение 8 минут протекания реакции количество вещества А в реакторе уменьшилось с 5,6 моль, до 4,4 моль. Объем реакционной массы составлял 56 л. Вычислить среднюю скорость химической реакции за исследованный промежуток времени
по веществам А, В и D.
Решение. Используем формулу в соответствии с определением понятия «средняя скорость химической реакции» и подставляем численные значения, получая среднюю скорость по реагенту А:
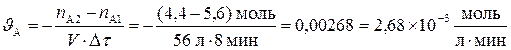 .
.
Из уравнения реакции следует, что по сравнению со скоростью убыли вещества А скорость убыли вещества В вдвое больше, а скорость увеличения количества продукта D — втрое больше.
Следовательно:
υ(А) = ½υ(В) =⅓υ(D)
и тогда υ(В) = 2υ(А) = 2·2,68·10–3 = 6, 36·10–3 моль·л–1·мин–1;
υ(D) = 3υ(А) = 3·2,68·10–3 = 8, 04·10–3 моль·л–1·мин–1.
Ответ: υ(А) =2,68·10–3 моль·л–1·мин–1;
υ(В) = 6, 36·10–3 моль·л–1·мин–1; υ(D) = 8, 04·10–3 моль·л–1·мин–1.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Содержание работы:
1. После ознакомления с теоретическим материалом выполнить нижеприведенные опыты 1 и 2 и записать данные о времени прохождения реакции (τ) в соответствующие столбцы таблиц.
2. На основании полученных данных рассчитать скорость реакции υ для каждого случая концентрации или температуры.
3. Построить графики зависимости скорости реакции от концентрации реагирующих веществ и температуры.
4. Произвести расчеты величины температурного коэффициента γ по данным опыта 2.
5. Сделать выводы о влиянии концентрации реагирующих веществ и температуры на скорость химических реакций.
