Энтропия. Второй закон термодинамики
Самопроизвольные процессы.В природе физические и химические превращения совершаются в определенном направлении. Так, два тела, находящиеся при разных температурах, вступают в контакт, тепловая энергия передается от более теплого тела к более холодному до тех пор, пока температура этих двух тел не сравняется. При погружении цинковой пластинки в соляную кислоту образуется ZnCl2 и H2. Все эти превращения являются самопроизвольными (спонтанными). Самопроизвольный процесс не может протекать в обратном направлении так же самопроизвольно, как в прямом.
В химии важно знать критерии, позволяющие предвидеть, может ли химическая реакция происходить самопроизвольно, и если может, то уметь определить количества образовавшихся продуктов. Первый закон термодинамики такого критерия не дает. Тепловой эффект реакции не определяет направления процесса. Самопроизвольно могут протекать как экзотермические, так и эндотермические реакции. Так, например, самопроизвольно идет процесс растворения нитрата аммония NH4NO3 (к) в воде, хотя тепловой эффект этого процесса положителен: 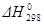 > 0 (процесс эндотермический); тоже самое можно сказать и о растворении гипосульфита натрия в воде. А в другом примере невозможно осуществить при Т = 298 К и p = 101 кПа (1 атм) синтез н. гептана C7H16 (ж), несмотря на то, что стандартная теплота его образования отрицательна:
> 0 (процесс эндотермический); тоже самое можно сказать и о растворении гипосульфита натрия в воде. А в другом примере невозможно осуществить при Т = 298 К и p = 101 кПа (1 атм) синтез н. гептана C7H16 (ж), несмотря на то, что стандартная теплота его образования отрицательна: 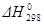 < 0 (процесс экзотермический).
< 0 (процесс экзотермический).
Таким образом, разность энтальпий реакции еще не определяет возможности ее протекания в данных конкретных условиях.
Второй закон термодинамики. Критерий самопроизвольного протекания процесса в изолированных системах дает второй закон термодинамики.
Второй закон термодинамики дает возможность разделить все допускаемые первым законом процессы на самопроизвольные и не самопроизвольные.
Второй закон термодинамики является постулатом, обоснованным большим опытом, накопленным человечеством. Он выражается разными эквивалентными формулировками:
1. Теплота не может переходить сама собой от менее нагретого тела к более нагретому - постулат Клаузиуса (1850 г). Утверждается, что процесс теплопроводности необратим.
2. Быстро или медленно всякая система стремится к состоянию истинного равновесия.
3. Невозможен периодический процесс, единственным результатом которого является превращение теплоты в работу - формулировка Кельвина - Планк.
4. Теплота может переходить в работу только при наличии разности температур и не целиком, а с определенным термическим коэффициентом полезного действия:
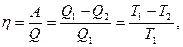
где η - термический коэффициент полезного действия; A – работа, полученная системой за счет перехода тепла от тела с высокой температурой (T1) к телу с низкой температурой (T2); Q1 – теплота, взятая у тела нагретого с температурой T1; Q2 – теплота, отданная холодному телу с температурой T2. Т.е. любые процессы протекают под действием разности потенциалов, каковой для тепловых процессов является разность температур, для электрических разность потенциалов, для механических - разность высот и т.д. Общим является сравнительно низкий коэффициент полезного действия. Значение к. п. д. обращается в единицу, если T2 → 0, но абсолютный нуль недостижим (третье начало термодинамики), следовательно, всю энергию нагретого тела при T1 в работу превратить нельзя. Т.е. при совершении работы часть общей энергии системы остается неиспользованной.
Понятие об энтропии.Исследуя выражение к.п.д. тепловой машины Клаузиус ввел новую термодинамическую функцию, которую назвал энтропией – S.
Работа идеальной тепловой машины (цикл Карно) подробно рассматривается в курсе физики.
Из математического выражения второго закона термодинамики следует:
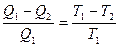 или
или 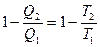
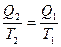 или
или 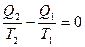
В дифференциальной форме:
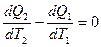
Суммируя изменения по всему циклу тепловой машины, получаем выражение 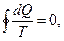 где dQ – приращение тепла, T – соответствующая температура;
где dQ – приращение тепла, T – соответствующая температура; 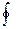 - интеграл по замкнутому контуру.
- интеграл по замкнутому контуру.
Подинтегральное выражение Клаузиус принял за приращение новой функции S – энтропии:
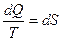 или
или 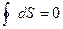
Энтропия представляет собой функцию параметров состояния системы (p, V, T) и может оценить направление процесса в системе, стремящейся к равновесию, т.к. для равновесного процесса ее изменение равно нулю; 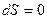 или
или 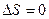 .
.
В случае необратимого превращения, т.е. спонтанного процесса, идущего при постоянной температуре, имеем 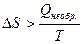
Если протекает процесс самопроизвольно, то изменение энтропии положительно: 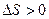
Для изолированных систем процессы, для которых изменение энтропии < 0, запрещены.
Если в качестве изолированной системы выбрать вселенную, то второе начало термодинамики можно сформулировать следующим образом:
Существует функция S, называемая энтропией, которая является такой функцией состояния, что
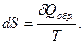
В случае обратимого процесса энтропия вселенной постоянна, а в случае необратимого процесса возрастает. Энтропия вселенной не может уменьшаться”.
Статистическая интерпретация энтропии.Для характеристики состояния некоторой массы вещества, являющейся совокупностью очень большого числа молекул можно указать параметры состояния системы и таким образом охарактеризовать макросостояние системы; но можно указать мгновенные координаты каждой молекулы (xi, yi, zi) и скорости перемещения по всем трем направлениям Vxi, Vyi, Vzi, т.е. охарактеризовать микросостояние системы. Каждому макросостоянию отвечает огромное число микросостояний. Число микросостояний, соответствующее макроскопическому состоянию определяется точными величинами параметров состояния и обозначается через W- термодинамическая вероятность состояния системы.
Термодинамическая вероятность состояния системы, состоящей всего из 10 молекул газа примерно 1000, а ведь только в 1 см3 газа содержится 2,7 ∙ 1019 молекул (н.у.). Поэтому в термодинамике используют не величину W, а ее логарифм lnW. Последнему можно придать размерность (Дж/К), умножив на константу Больцмана К:
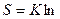 W, где
W, где 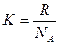 =1, 38 · 10-23 Дж/К,
=1, 38 · 10-23 Дж/К,
где NA – число Авогадро
Величину S называют энтропией системы. Энтропия – термодинамическая функция состояния системы.
Если изолированная система находится в макроскопическом состоянии 1, соответствующем W1 микроскопических состояний и если она может перейти в макроскопическое состояние 2, число микроскопических состояний которого W2, то система будет иметь тенденцию перейти в состояние 2 при условии, что W2 > W1
Система спонтанно стремится к состоянию, которому в микроскопическом масштабе соответствует наибольшее число возможностей реализации.
Например, при расширении идеального газа в пустоту конечное состояние (с большим объемом по сравнению с начальным состоянием) включает гораздо большее число микросостояний просто потому, что молекулы могут принимать большее число положений в пространстве.
Когда в изолированной системе происходит самопроизвольный процесс, число микроскопических состояний W возрастает; тоже самое можно сказать об энтропии системы. При возрастании числа микроскопических состояний W, связанных с макроскопическим состоянием системы, энтропия увеличивается.
Например, рассмотрим термодинамическое состояние 1 моль воды (18 г H2O) при стандартных условиях. Пусть W (ж) - термодинамическая вероятность состояния этой системы. При понижении температуры до 0 ºС вода замерзает, превращается в лед; при этом молекулы воды как бы закрепляются в узлах кристаллической решетки и термодинамическая вероятность состояния системы уменьшается; W (к) < W (ж). Следовательно, падает и энтропия системы: 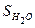 (к) <
(к) < 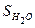 (ж). Наоборот при повышении температуры до 100º С вода закипает и превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается: W (г) > W (ж), следовательно, растет и энтропия системы:
(ж). Наоборот при повышении температуры до 100º С вода закипает и превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается: W (г) > W (ж), следовательно, растет и энтропия системы:
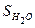 (г) >
(г) > 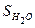 (ж).
(ж).
Энтропия, таким образом, является мерой неупорядоченности состояния системы. Действительно, единственному микроскопическому состоянию (W = 1) будет соответствовать полная упорядоченность и нулевая энтропия, т.е. известны положение, скорость, энергия каждой частицы, и все эти микроскопические характеристики будут оставаться постоянными во времени.
Второй закон термодинамики можно сформулировать следующим образом:
Изолированная система стремится достигнуть наиболее вероятного состояния, т.е. макроскопического состояния, соответствующего наибольшему числу микроскопических состояний.
В изолированных системах самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии системы: Δ S > 0 (Δ S = S2 – S1).
Энтропия чистых веществ, существующих в виде идеальных кристаллов при температуре абсолютного нуля равна нулю. Это значит, что при абсолютном нуле достигается полная упорядоченность.
Третий закон термодинамики
Этот закон позволяет приписать абсолютную энтропию всем чистым веществам при любой температуре.
Величины абсолютной энтропии 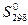 (стандартная энтропия в основном приводится при температуре 298 К и атмосферном давлении и) выражаются в кал/моль К или в энтропийных единицах (э.е.). Для твердых тел величина абсолютной энтропии в среднем равна 10 – 15 э.е. Величина 0,6 э.е. для алмаза свидетельствует о весьма жесткой упорядоченной структуре.
(стандартная энтропия в основном приводится при температуре 298 К и атмосферном давлении и) выражаются в кал/моль К или в энтропийных единицах (э.е.). Для твердых тел величина абсолютной энтропии в среднем равна 10 – 15 э.е. Величина 0,6 э.е. для алмаза свидетельствует о весьма жесткой упорядоченной структуре.
Поскольку можно рассчитать абсолютную энтропию чистых веществ при любой T, можно определить изменение энтропии Δ S для любой химической реакции. Энтропия – функция состояния, поэтому изменение энтропии равно разности между величинами абсолютной энтропии продуктов и реагентов при температуре и давлении, при которых протекает реакция.
Так, для химической реакции
aA + bB +…= dD + eE +…
Изменение энтропии будет
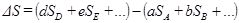 или
или 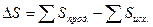
Например, изменение энтропии Δ 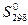 в стандартных условиях для реакции образования хлороводорода рассчитывается следующим образом:
в стандартных условиях для реакции образования хлороводорода рассчитывается следующим образом:
H2 (г) + Cl2 (г) = 2HCl (г)
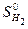 = 130,58 Дж/моль К;
= 130,58 Дж/моль К; 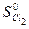 = 222,96 Дж/моль ∙ К;
= 222,96 Дж/моль ∙ К;
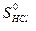 = 186,69 Дж/моль ∙ К
= 186,69 Дж/моль ∙ К
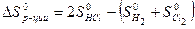
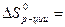 2 ∙ 186,69 – (130,58 + 222,96) = 19,84 Дж/К
2 ∙ 186,69 – (130,58 + 222,96) = 19,84 Дж/К
Изменение энтропии, сопровождающее эту реакцию невелико, поскольку реакция протекает в газовой фазе без изменения числа газообразных молекул.
Если изменение энтальпии ∆ H отражает в основном стремление атомов к объединению в молекулу, т.к. к укрупнению, агрегации, определенному порядку, то величина ∆ S отражает противоположную тенденцию: стремление частиц к разъединению, дроблению, беспорядку.
Движущей силой процесса, протекающего в изобарно – изотермических условиях может быть или стремление системы перейти в состояние с наименьшей энергией, т.е. выделить теплоту в окружающую среду, уменьшить энтальпию (стремление к порядку), или стремление системы перейти в состояние с наибольшей термодинамической вероятностью, т.е. увеличить энтропию (стремление к беспорядку). Если процесс протекает так, что ∆ H = 0, то рост энтропии становится его единственной движущей силой. И, наоборот, при условии ∆ S = 0 единственной движущей силой процесса является убыль энтальпии. В связи с этим можно говорить об энтальпийном ∆ H и энтропийном T ∆S факторах процесса, равенству которых ∆ H = T ∆ S отвечает наиболее устойчивое при данных условиях равновесное состояние системы. Вывести эту систему из равновесного состояния можно только внешним воздействием (изменением T, p и т.п.)
