Обработка двухпараметрических зависимостей

Постановка задачи. Пусть имеется n пар значений (x_i, y_i), которые отвечают линейной зависимости y = a + bx, причем каждое из x_i и y_i измерено с некоторой погрешностью, из-за чего экспериментальные результаты точно на прямую не попадают (рис. 1). Необходимо найти параметры a и b линейной зависимости, наилучшим образом проходящей через экспериментальные точки в целом (возможно, не проходя ни через одну из них).

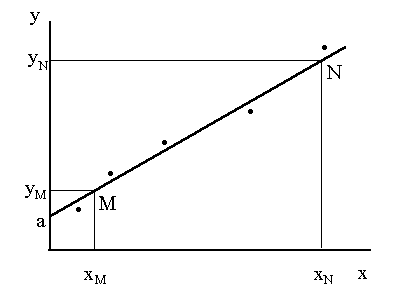
Рис. 1. Обработка результатов графическим методом

Порядок расчета. В настоящее время наибольшей популярностью у химиков пользуются два метода определения параметров линейной зависимости (линейной регрессии): графический метод и метод наименьших квадратов.

Для обработки результатов графическим методом используют миллиметровую бумагу, на которую в виде графика наносят экспериментальные данные в строгом соответствии с выбранным масштабом. При выборе масштаба осей графика для нанесения 3 - 4 делений на каждую из осей координат руководствуются тем, чтобы интервал изменения абсцисс и ординат экспериментальных точек соответствовал отметкам в начале и конце осей координат. Для построения удобного для расчета графика не нужно стремиться к появлению нуля или другого конкретного значения в точке пересечения осей. При разбиении оси на отрезки равной длины и нанесения соответствующих делений число клеточек между делениями выбирают таким образом, чтобы оно было кратно разности координат, соответствующих этим делениям.

После расчета цены деления осей на график наносят экспериментальные данные в виде точек. Затем через экспериментальные точки проводят прямую (на глаз, как можно ближе к нанесенным точкам, как показано на рис. 1). Далее на этой прямой выбирают две любые точки M и N, желательно достаточно удаленные друг от друга. Отсчитав по осям их координаты (x_M, y_M) и (x_N, y_N), рассчитывают тангенс угла наклона прямой по формуле

.

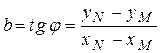Это значение совпадает с угловым коэффициентом b искомой прямой. При желании значение параметра a можно найти, продлив проведенную прямую до пересечения с осью ординат и отсчитав координату y этой точки (рис. 1).

Использование метода наименьших квадратов не требует построения графика. Расчет параметров линейной зависимости производится только лишь на основании координат экспериментальных точек по формулам:

.

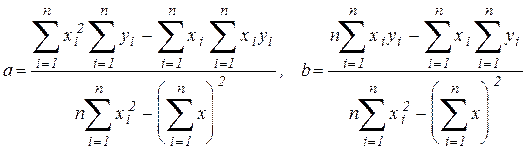В том случае если двухпараметрическая зависимость не является линейной, то, проведя тождественные преобразования, можно получить такую зависимость некоторых других функций связываемых переменных, которая будет иметь уже линейный вид. Такие преобразования называются линеаризующими. В результате их выполнения нелинейная зависимость y = f(x) примет видя j(x, y) = a + by(x, y). После вычисления соответствующих функций j(x_i, y_i) и y(x_i, y_i) и замены переменных задача сводится к описанной выше.

В лабораторной работе "Скорость химических реакций" производится обработка экспериментальных данных зависимости скорости реакции от концентрации реагирующих веществ с целью расчета порядка реакции и зависимости скорости реакции от температуры с целью вычисления температурного коэффициента скорости или энергии активации.

Нахождение любой из трех названных величие выполняется и графическим методом, и методом наименьших квадратов. Такой расчет включает вычисление параметра b линейной зависимости, после чего из найденного значения b рассчитывается либо порядок реакции, либо температурный коэффициент скорости реакции, либо энергия активации. Параметр a линейной зависимости позволяет объединить все другие неизменные в ходе опыта величины в некоторую константу, вычислять которую не требуется.

Конкретный порядок расчета, включающий преобразование расчетного выражения логарифмированием, выделение параметров a и b линейной зависимости, замену переменных, внешний вид графика и таблицы, упрощающей расчет параметра b методом наименьших квадратов, изложен в трех следующих примерах.

Пример 1. Зависимость скорости реакции взаимодействия тиосульфата натрия и серной кислоты от концентрации реагирующих веществ отражается законом действующих масс:

.

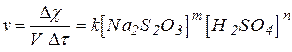После логарифмирования этого выражения и соответствующей группировки слагаемых имеем:

.

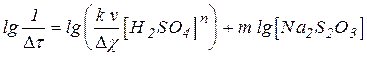Методика выполнения измерений, приведенная в описании лабораторной работы "Скорость химических реакций и химическое равновесие", обеспечивает постоянство всех величин, указанных в круглых скобках этого выражения. Следовательно, зависимость lg (1 / Dt) от lg [ Na₂S₂O₃ ] является линейной и угловой коэффициент этой линейной зависимости равен порядку реакции по тиосульфату натрия. Полагая x_i = lg [Na₂S₂O₃]_i и y_i = lg (1 / Dt)_i, заключаем, что

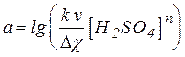и b = n.

Следовательно, построение графика зависимости y_i = lg (1 / Dt)_i от x_i = lg [Na₂S₂O₃]_i (рис. 2) и расчет тангенса угла наклона позволяет получить непосредственно значение порядка реакции. Значения координат точек (x_i, y_i) для нанесения их на график удобно заимствовать из табл. 1. Этой же таблицей удобно пользоваться для расчета порядка реакции методом наименьших квадратов.

Замечание. Расчет текущих концентраций С тиосульфата натрия в растворе после разбавления проводят, принимая во внимание, что исходный раствор Na₂S₂O₃ концентрации 0.1 н. соответствует C₀ = 0.05 M раствору. Поскольку количество вещества тиосульфата натрия до и после смешивания его с другими реагентами не изменяется, то

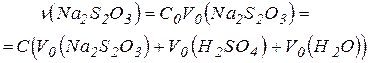
где V₀ - объемы добавляемых растворов.

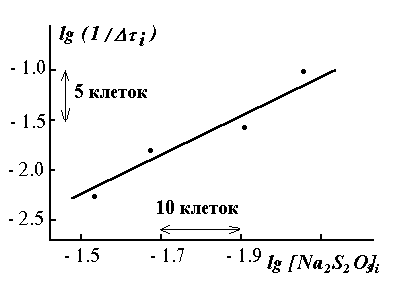
Рис. 2. Примерный вид графика для расчета порядка реакции

i	[Na2S2O3]i	Dti	xi = lg [Na2S2O3]i	yi = lg 1/Dti	xi2	xiyi
Сумма

Табл. 1. Расчет порядка реакции методом наименьших квадратов.

Пример 2. Зависимость скорости реакции от температуры может быть представлена уравнением Вант-Гоффа:

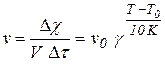
Прологарифмировав это выражение и раскрыв скобки, получаем:

,

,

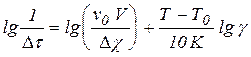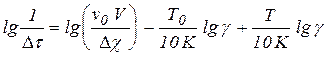Полагая

,

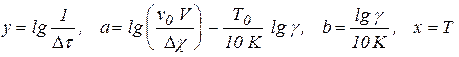приходим к линейной зависимости y = a + bx, которую можно обработать как графически (рис. 3), так и методом наименьших квадратов. После вычисления углового коэффициента прямой (тангенса угла наклона) можно найти температурный коэффициент скорости из выражения для b, приведенного выше, а именно: g = 10^10b.

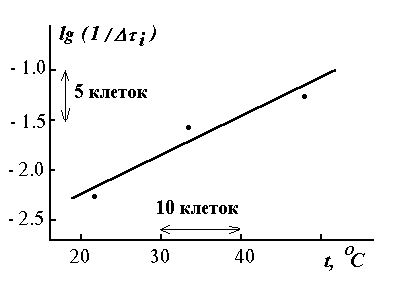
Рис. 3. Примерный вид графика для расчета температурного коэффициента скорости реакции

При построении графика по вертикальной оси следует откладывать y_i = lg (1/Dt_i), а по горизонтальной - x_i = t_i. Расчет методом наименьших квадратов удобно осуществлять, заполняя таблицу 2.

i	Ti	Dti	xi = Ti	yi = lg 1/Dti	xi2	xiyi
Сумма

Табл. 2. Расчет температурного коэффициента скорости реакции методом наименьших квадратов

Пример 3. Зависимость скорости реакции взаимодействия тиосульфата натрия и серной кислоты от температуры выражается уравнением Аррениуса:

.

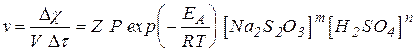Прологарифмировав это выражение и сгруппировав слагаемые, получаем:

.

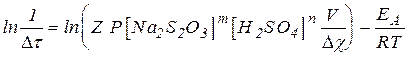Введя обозначения

,

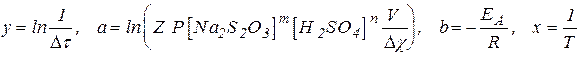приходим к линейной зависимости y = a + bx, которую можно обработать как графически, так и методом наименьших квадратов. После вычисления углового коэффициента прямой можно найти энергию активации реакции из выражения для b, приведенного выше: E_A = - bR.

При построении графика (рис. 4) по вертикальной оси следует откладывать y_i = lg (1/Dt_i), а по горизонтальной - x_i = 1/T_i. Расчет методом наименьших квадратов удобно осуществлять, заполняя таблицу 3.

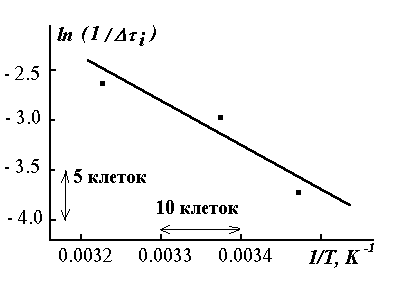
Рис. 4. Примерный вид графика для расчета энергии активации

i	Ti	Dti	xi = 1/Ti	yi = ln 1/Dti	xi2	xiyi
Сумма

Табл. 3. Расчет энергии активации реакции методом наименьших квадратов