Внутренняя энергия и первый закон термодинамики. Энтальпия
Термодинамика - это наука, изучающая переходы энергии из одной формы в другую и от одной части системы к другой при протекании различных процессов. Раздел термодинамики, изучающий системы, в которых происходят химические реакции и фазовые переходы, называется химической термодинамикой.
Для характеристики состояния системы термодинамика использует так называемые термодинамические функции, к которым относятся внутренняя энергия (U), энтальпия (H), энтропия (S), свободная энергия Гиббса (G). Общим для термодинамических функций является то, что все они являются функциями состояния: изменение термодинамической функции зависит только от начального и конечного состояния системы и не зависит от пути, по которому протекает данный процесс. Остановимся на характеристике первых двух термодинамических функций.
Внутренняя энергия (U) - это совокупность всех видов энергии термодинамической системы, кроме кинетической энергии ее движения как целого и потенциальной энергии ее положения в каком-либо внешнем поле.
Во внутреннюю энергию входят энергия движения тел, образующих систему, энергия движения молекул, атомов, ионов, электронов, внутриядерная энергия и т.д. Поскольку во внутреннюю энергию входят все виды энергии, заключенные в материи, в том числе и те, о которых мы ничего не знаем, абсолютные значения внутренней энергии не могут быть определены. Однако можно определить изменение внутренней энергии в результате какого-либо процесса:
ΔU = U2 - U1,
где U1 и U2 - внутренняя энергия процесса в начальном и конечном состояниях системы.
Пусть система представляет собой сосуд, в котором свободно движется поршень, оказывающий давление (р) на газ, находящийся внутри сосуда. В системе протекают процессы, сопровождающиеся выделением или поглощением теплоты. Если эти процессы являются химическими реакциями или фазовыми переходами, то количество теплоты, поглощаемое системой, называется тепловым эффектом реакции или фазового перехода (Q). Реакции, протекающие с поглощением тепла (Q < 0), называются эндотермическими, с выделением тепла (Q > 0) - экзотермическими. Если поршень в сосуде движется свободно, процесс протекает при постоянном давлении (изобарный процесс с тепловым эффектом Qp). Если поршень фиксирован, процесс осуществляется при постоянном объеме (изохорный процесс с тепловым эффектом QV).
Пусть в системе имеет место эндотермическая реакция (Q > 0). В этом случае поглощенная системой теплота может израсходоваться на увеличение внутренней энергии системы на величину ΔU и на совершение работы А против внешних сил (например, на поднятие поршня). В соответствии с законом сохранения энергии:
Q = ΔU + A или ΔU = Q – А
Приведенное выше уравнение является математическим выражением первого закона термодинамики: увеличение внутренней энергии системы равно количеству теплоты, сообщенной системе, минус количество работы, совершенной системой против внешних сил.
Значения ΔU и А могут быть как положительными, так и отрицательными; в последнем случае внутренняя энергия системы понижается, а внешние силы совершают определенную работу.
Совершаемую системой работу можно представить как сумму двух величин:
А = А(р) + А',
где А(р) - работа, совершенная против внешнего давления, А' - все другие виды работы (например, работа, связанная с электрическим или магнитным полем). Рассмотрим случай, когда А' = 0. Тогда:
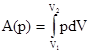
Если реакция протекает при постоянном объеме, то V1 = V2 и А(р) = 0, откуда QV = ΔU.
Таким образом, тепловой эффект изохорного процесса равен изменению внутренней энергии системы.
Если в процессе реакции постоянным остается давление, то
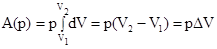 , Qp = ΔU + pΔV
, Qp = ΔU + pΔV
Подставив в уравнение значения ΔU и ΔV, получаем:
Qp = (U2 - U1) + p(V2 -V1) = (U2 + pV2) - (U1 + pV1);
Qp = H2 - H1 = ΔH,
где H = U + pV - термодинамическая функция, называемая энтальпией. Таким образом, тепловой эффект изобарного процесса равен изменению энтальпии системы.
Отметим, что энтальпия, как и внутренняя энергия, является функцией состояния и определяется лишь начальным и конечным состоянием системы, но не зависит от пути, по которому протекает процесс. Поскольку в выражение энтальпии входит внутренняя энергия, абсолютное значение Н неопределимо. В связи с тем, что химические реакции часто проводят при постоянном давлении, энтальпия широко используется для выражения тепловых эффектов.
Термохимия. Закон Гесса
Термохимия - раздел химической термодинамики, рассматривающий тепловые эффекты реакций и связанные с ними расчеты. Такие расчеты выполняют с использованием термохимических уравнений, которые отличаются от обычных химических уравнений следующими особенностями:
1. Коэффициенты в термохимических уравнениях указывают не число атомов и молекул, участвующих во взаимодействии, а количества вещества. В силу этого в подобных уравнениях допустимо использование дробных коэффициентов, которые обычно подбирают таким образом, чтобы коэффициент перед целевым продуктом реакции равнялся единице.
2. В термохимических уравнениях указывается тепловой эффект реакции (обычно величина ΔН). Тепловой эффект при этом относят к числу молей реагентов и продуктов реакции, определяемых коэффициентами уравнения, и выражают в кДж.
3. В термохимических уравнениях обязательно указывают агрегатное состояние реагентов и продуктов реакции, поскольку фазовые переходы сопровождаются выделением или поглощением энергии. Агрегатное состояние вещества обозначают сокращениями: к - кристаллическое, ж - жидкое, г - газообразное, р - растворенное.
Тепловые эффекты обычно относят к стандартным условиям (температура 298 К, давление 1,01325.105 Па); стандартные энтальпии обозначают символом 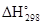 .
.
Термодинамические уравнения более информативны, чем обычные химические уравнения. Так, из уравнения реакции:
2Н2 + О2 = 2Н2О
следует, что из двух молекул водорода и одной молекулы кислорода образуются две молекулы воды. Термохимическое уравнение этой реакции имеет следующий вид:
2Н2(г) + О2(г) = 2Н2О(г); 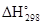 = -483,64 кДж
= -483,64 кДж
Из него следует, что при образовании двух молей водяного пара из двух молей водорода и моля кислорода в газообразном состоянии выделяется 483,64 кДж теплоты при стандартных условиях. Если расчет имеет целью определить тепловой эффект образования моля газообразной воды, уравнение можно записать так:
Н2(г) + 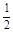 О2(г) = Н2О(г);
О2(г) = Н2О(г); 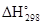 = -241,83 кДж/моль
= -241,83 кДж/моль
Поскольку термохимические уравнения и их тепловые эффекты относят к макроколичествам веществ, с ними можно выполнять разнообразные алгебраические операции: их можно складывать, вычитать, умножать на некоторые величины и т.д.
Основным законом термохимии, на основании которого проводят термохимические расчеты, является закон, сформулированный Г. И. Гессом в1841 г.: тепловой эффект химической реакции определяется начальным и конечным состоянием системы и не зависит от пути проведения процесса и числа промежуточных стадий.
Например, если реакцию
А(г) + 2В(г) = АВ2(г); ΔН1
провести в две стадии
А(г) + В(г) = АВ(г); ΔН2,
АВ(г) + В(г) = АВ2(г); ΔН3,
то сумма тепловых эффектов отдельных стадий будет равна тепловому эффекту суммарной реакции
ΔН1 = ΔН2 + ΔН3
Связь между тепловыми эффектами химической реакции и ее отдельных стадий может быть представлена наглядно с помощью энтальпийных диаграмм. На энтальпийных диаграммах значениям энтальпии для различных состояний системы соответствуют ступеньки, расстояние между которыми равны тепловым эффектам перехода из одного состояния в другое (рис. 14); стрелки, направленные вниз, соответствуют выделению энергии, стрелки, направленные вверх, - ее поглощению.
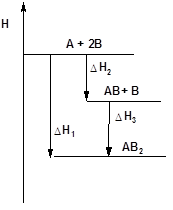
Рис. 14. Энтальпийная диаграмма для реакции А + 2В = АВ2.
Закон Гесса позволяет решать многие практически важные задачи. Прежде всего отметим, что этот закон позволяет выражать тепловые эффекты реакций через энтальпии образования веществ, участвующих во взаимодействии.
Энтальпия образования - это изменение энтальпии системы при синтезе одного моля вещества из простых веществ. Эта величина обозначается символом ΔНf. Если процесс протекает в стандартных условиях, энтальпию образования называют стандартной ( 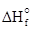 ). Значения стандартных энтальпий образования для различных соединений приводятся в термодинамических справочниках.
). Значения стандартных энтальпий образования для различных соединений приводятся в термодинамических справочниках.
Энтальпии простых веществ по определению равны нулю. Если элемент образует несколько простых веществ, то равным нулю принимается значение 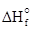 для той аллотропной модификации, которая при стандартных условиях наиболее устойчива (например, графит в случае углерода).
для той аллотропной модификации, которая при стандартных условиях наиболее устойчива (например, графит в случае углерода).
Конкретные термохимические расчеты выполняют на основании следствий из закона Гесса.
Следствие первое - с термохимическими реакциями можно выполнять арифметические операции. Таким образом, комбинируя термохимические уравнения, можно определять тепловые эффекты любых реакций, в том числе и тех, для которых его определение связано с экспериментальными сложностями или вообще невыполнимо. Например, невозможно экспериментально определить тепловой эффект реакции образования оксида углерода(II):
С(графит) + 1/2О2(г) = СО(г),
поскольку большое сродство углерода к кислороду приводит к образованию примеси СО2 даже при недостатке кислорода. В то же время легко поддаются экспериментальному определению тепловые эффекты следующих реакций:
С(графит) + О2(г) = СО2(г); DHо1 = -393,5 кДж;
СO(г) + 1/2O2(г) = CO2(г); DHо2 = -283 кДж
Вычтя второе уравнение из первого, получим уравнение образования оксида углерода(II):
С(графит) + О2(г) - СO(г) + 1/2O2(г) = СО2(г) - СО2(г);
С(графит) - СO(г) + 1/2O2(г) = 0;
С(графит) + 1/2O2(г) = СO(г)
Соответствующая комбинация тепловых эффектов реакций дает искомый тепловой эффект
DHо = DHо1 - DHо2 = -393,5 - (-283) = -110,5 (кДж)
Следствие второе - тепловой эффект химической реакции равен разности сумм энтальпий образования продуктов реакции и энтальпий образования исходных веществ.
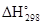 =
= 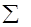 i
i 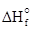 (пр) -
(пр) - 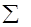 j
j 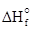 (реаг),
(реаг),
где i и j – коэффициенты в термохимическом уравнении.
Применение данного следствия позволяет рассчитать тепловой эффект любой реакции, для которой известны стандартные энтальпии образования реагентов и продуктов реакции (справочные данные).
Рассчитаем в качестве примера тепловой эффект реакции термического разложения карбоната кальция:
CaCO3(к) = CaO(к) + CO2(г);
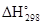 =
= 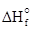 (CaO) +
(CaO) + 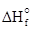 (CO2) -
(CO2) - 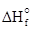 (CaCO3);
(CaCO3);
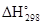 = -635,5 + (-393,5) - (-1206,9) = 177,9 (кДж)
= -635,5 + (-393,5) - (-1206,9) = 177,9 (кДж)
Следствие третье - тепловой эффект химической реакции равен разности сумм энтальпий сгорания исходных веществ и энтальпий сгорания продуктов реакции.
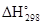 =
= 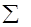 i
i 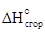 (реаг) -
(реаг) - 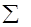 j
j 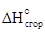 (пр)
(пр)
В качестве примера рассчитаем энтальпию процесса перехода цис-бутена-2 в транс-изомер:
cis-С4Н8 ® trans-C4H8
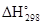 =
= 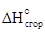 (cis-C4H8) -
(cis-C4H8) - 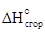 (trans-C4H8);
(trans-C4H8); 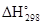 = -2710,4 - (-2706,2) = -4,2 (кДж)
= -2710,4 - (-2706,2) = -4,2 (кДж)
