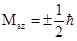Квантово-механическое описание одноэлектронных частиц

Волновая функция имеет сложный вид, поэтому решение уравнения Шредингера связано с колоссальными сложностями. Строго оно может быть решено только для одноэлектронных частиц, например, для атома водорода. Решение уравнения Шредингера даже для столь простых систем привело к двум интересным следствиям:

1. Решения имеют дискретный характер и представляют собой набор волновых функций и соответствующих им дискретных (квантованных) значений энергии атома.

2. Волновые функции включают целочисленные параметры, изменяющиеся на единицу - квантовые числа. Поэтому орбитали атома водорода можно качественно описать с помощью набора квантовых чисел. Каждое квантовое число играет важную роль, обеспечивая квантование (дискретность) определенной физической величины.

Главное квантовое число (n) изменяется дискретно, принимая значения 1, 2, 3, ..¥. Главное квантовое число характеризует прежде всего энергетический уровень электрона, энергия которого определяется следующим выражением:

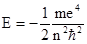
Поскольку масса и заряд электрона постоянны, энергия последнего зависит только от квантового числа. Как следует из приведенного выше уравнения, максимальное значение Е соответствует n = ¥ и равно нулю. Эта энергия отвечает удалению электрона на бесконечно большое расстояние от ядра, т.е. ионизации атома водорода. Все остальные разрешенные значения энергии отрицательны, минимальное из них составляет

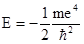= -1,31×10³ кДж/моль

Главное квантовое число характеризует среднюю удаленнось электрона от ядра. Совершенно очевидно, что орбиталь не имеет строгих размеров в обычном понимании этого слова, так как электрон с разной вероятностью может находиться в любой точке пространства. Поместим ядро атома в центр координат, разобьем окружающее его пространство на множество тончайших сферических слоев. Объем такого слоя, отстоящего от ядра на расстояние r, будет равен 4pr²dr, где dr - толщина слоя. Тогда, в соответствии с физическим смыслом квадрата волновой функции, вероятность нахождения электрона в таком слое составит:

dW = 4pr²y²dr

Если построить зависимость 4pr²y² от r, то мы получим график функции радиального распределения вероятности нахождения электрона на разных удалениях от ядра. Примеры приведены на рис. 2. Вероятность нахождения электрона имеет один или несколько максимумов, отвечающих расстояниям, на которых электрон находится наиболее часто. Если на графике f(r)= 4pr²y² максимумов несколько, то самый высокий из них будет расположен тем дальше от ядра, чем больше значение главного квантового числа.

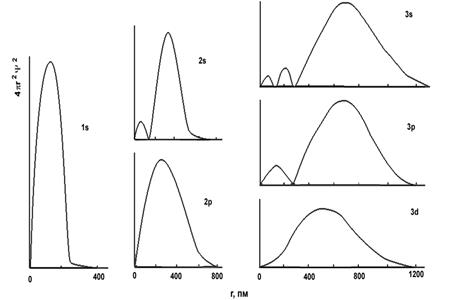
Рис. 2. Кривые радиального распределения вероятности нахождения электрона для некоторых орбиталей атома водорода.

Орбитальное квантовое число (l) для заданного значения n принимает целочисленные значения от 0 до (n-1). Значение l обозначается буквами в следующем порядке

l 0 1 2 3 4 5

Обозначение s p d f g h

Соответственно, орбитали, для которых l = 0 называются s-орбиталями, l = 1 - р-орбиталями и т.д.

Орбитальное квантовое число характеризует энергетические подуровни атома. Сколько значений принимает l в пределах заданного значения n, столько подуровней включает данный энергетический уровень. Так, первый уровень (n = 1) содержит один s-подуровень (l = 0). Второй уровень включает два подуровня s и p (l = 0 и 1), третий - три подуровня s, p и d, (l = 0, 1 и 2) и т.д.

От орбитального квантового числа зависят также значения, которые может принимать орбитальный момент импульса электрона. Орбитальным моментом импульса называется векторное произведение радиус-вектора и импульса электрона:

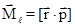
Как всякий вектор, момент импульса характеризуется абсолютной величиной (модулем M_l) и направлением, определяемым проекциями M_l на координатные оси. Орбитальное квантовое число квантует значения M_l в соответствии с уравнением:

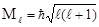
Так, для s-подуровней модуль момента импульса равен нулю, для всех р-подуровней - 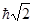и т.д.

Орбитальное квантовое число определяет форму граничной поверхности орбитали. Так, все s-орбитали имеют сферическую форму, р-орбитали - форму гантели (объемной восьмерки); форма d-орбиталей - либо объемная четырехлепестковая розетка, либо гантель в кольце. Формы орбиталей, отвечающих различным значениям l, приведены на рис. 3.

p_z p_x p_y

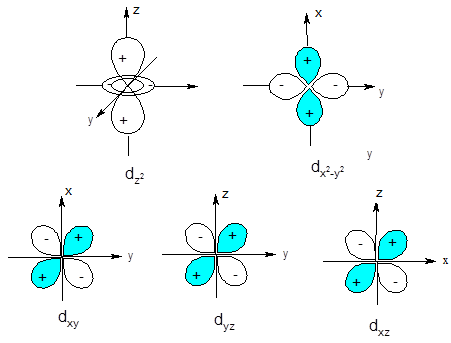
Рис. 3. Форма граничной поверхности s-, p- и d-орбиталей.

Главное и орбитальное квантовые числа совместно обуславливают вид кривой радиального распределения вероятности нахождения электрона: число максимумов на ней равно разности n-l. Например, для подуровня 1s (n = 1, l = 0) кривая радиальной вероятности имеет один максимум, для подуровня 2s (n = 2, l= 0) - два максимума, для подуровня 2p (n = 2, l= 1) - один максимум и т.д. (рис. 2).

Магнитное квантовое число (m_l). В пределах заданного значения l магнитное квантовое число принимает ряд значений: -l, …-2, -1, 0, +1, +2, ...l. Это квантовое число определяет ориентацию вектора 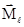в пространстве, квантуя проекцию вектора на одну из координатных осей, например, на ось z:

M_lz =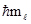

Определению проекций 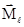на другие координатные оси препятствует принцип неопределенности: если бы это было возможно, то было бы установлено точное значение момента импульса электрона.

Характеризуя направление орбитального момента импульса, магнитное квантовое число тем самым определяет ориентацию электронной орбитали в пространстве. Сколько значений принимает m_l для заданного значения l, столько орбиталей, по-разному ориентированных в пространстве, возможно для данного подуровня (рис. 3). Так, для s-подуровня m_l принимает одно значение (m_l = 0), т.е. s-орбиталь может быть ориентирована в пространстве одним способом, а s-подуровень включает одну орбиталь. В случае р-подуровня m_l имеет три значения (0, ±1) и три р-орбитали этого подуровня ориентируются в пространстве тремя разными способами: по оси x (орбиталь p_x), по оси у (орбиталь p_y) и третья по оси z (орбиталь p_z). d-Подуровень включает пять орбиталей (m_l = 0, ±1, ±2), ориентированных относительно координатных осей пятью различными способами. Знаки (+) и (-) на рис. 3 указывают математический знак волновой функции для разных областей пространства.

Орбитали одного подуровня, отличающиеся значениями m_l, имеют одинаковые энергии. Число таких орбиталей определяет степень вырождения подуровня. Так, s-подуровень не вырожден, р-подуровень трехкратно вырожден, степень вырождения для d- и f-подуровней равна соответственно пяти и семи. В общем случае степень вырождения определяется следующей формулой:

С.В. = 2l + 1

При помещении атома в электрическое или магнитное поле, энергии орбиталей с одинаковыми значениями l, но разными значениями m_l становятся неодинаковыми, так как эти орбитали по-разному ориентированы относительно направления поля. Происходит снятие вырождения, соответственно чему линии в атомном спектре расщепляются.

Спиновое (s) и магнитное спиновое (m_s) квантовые числа. Квантовые числа n, l и m_l квантуют физические характеристики электрона, связанные с его поступательным движением. Однако электрон, кроме орбитального момента импульса, имеет еще и собственный момент импульса (спин), связанный с квантово-механическим аналогом вращательного движения, что обеспечивает четвертую степень свободы электрона. Как указывалось выше, для квантования орбитального момента импульса необходимы два квантовых числа (l и m_l); аналогично для квантования собственного момента импульса так же нужны два квантовых числа - спиновое (s), квантующее модуль момента (M_s), и магнитное спиновое (m_s), квантующее направление вектора 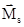. Экспериментально установлено, что в сильных электрических и магнитных полях любая орбиталь проявляет свойства двухкратно вырожденной.

С.В. = 2s + 1; s = 1/2

Таким образом, квантовое число s является полуцелым и одинаково для всех электронов. Проекция собственного момента импульса на направление магнитного поля имеет два значения, соответственно чему магнитное спиновое квантовое число принимает значения +1/2 (a-спин, ­) и -1/2 (b-спин, ¯).

Найденные значения s и m_s позволяют квантовать характеристики собственного момента импульса электрона:

;
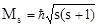