Стехиометрические законы химии

Закон сохранения массы (М.В. Ломоносов, 1748 г.). Сумма масс продуктов реакции равна сумме масс веществ, вступивших во взаимодействие. В математическом виде этот закон выражается следующим уравнением:

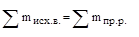
Дополнением к данному закону является закон сохранения массы элемента (А. Лавуазье, 1789 г.). Согласно этому закону в процессе химической реакции масса каждого элемента остается постоянной.

Законы М.В. Ломоносова и А. Лавуазье нашли простое объяснение в рамках атомистической теории. Действительно, при любой реакции атомы химических элементов остаются неизменными и в неизменном количестве, что влечет за собой как постоянство массы каждого элемента в отдельности, так и массы веществ в целом.

Рассматриваемые законы имеют определяющее значение для химии, поскольку позволяют описывать химические реакции уравнениями и выполнять на их основе количественные вычисления. Необходимо отметить, что закон сохранения массы не является абсолютно точным. Как следует из теории относительности (А. Эйнштейн, 1905 г.), любой процесс, протекающий с выделением энергии, сопровождается уменьшением массы системы в соответствии с уравнением:

DE = Dm×c²,

где DЕ – выделившаяся энергия, Dm – изменение массы системы, с - скорость света в вакууме (3,0×10⁸ м/с). В результате уравнение закона сохранения массы следует записывать в следующем виде:

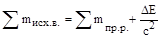
Таким образом, экзотермические реакции сопровождаются уменьшением массы, а эндотермические – увеличением массы. В этом случае закон сохранение массы может быть сформулирован следующим образом: в изолированной системе сумма масс и приведенных энергий есть величина постоянная. Однако для химических реакций, тепловые эффекты которых измеряются сотнями кДж/моль, дефект массы составляет 10^-8-10^-9 г и не может быть зарегистрирован экспериментально.

Закон постоянства состава (Ж. Пруст, 1799-1804 гг.). Индивидуальное химическое вещество молекулярного строения имеет постоянный качественный и количественный состав, не зависящий от способа его получения.

Соединения, подчиняющиеся закону постоянства состава, называют дальтонидами. Дальтонидами являются все известные к настоящему времени органические соединения (около 30 миллионов) и часть (около 100 тыс.) неорганических веществ. Вещества, имеющие немолекулярное строение (бертолиды), не подчиняются данному закону и могут иметь переменный состав, зависящий от способа получения образца. К бертолидам относится большинство (около 500 тыс.) неорганических веществ, в основном это бинарные соединения d-элементов (оксиды, сульфиды, нитриды, карбиды и т.д.). Примером соединения переменного состава может служить оксид титана(III), состав которого варьирует в пределах от TiO_1,46 до TiO_1,56. Причиной переменного состава и иррациональности формул бертолидов является изменение состава части элементарных ячеек кристалла (дефекты кристаллической структуры), не влекущее за собой резкого изменения свойств вещества. Для дальтонидов подобное явление невозможно, поскольку изменение состава молекулы ведет к образованию нового химического соединения.

Закон эквивалентов (И. Рихтер, Дж. Дальтон, 1792-1804 гг.). Массы реагирующих веществ прямо пропорциональны их эквивалентным массам.

,

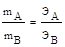где Э_А и Э_В - эквивалентные массы реагирующих веществ.

Эквивалентной массой вещества называется молярная масса его эквивалента.

Эквивалент - это реальная или условная частица, отдающая или присоединяющая один катион водорода в реакциях кислотно-основного взаимодействия, один электрон в окислительно-восстановительных реакциях или взаимодействующая с одним эквивалентом любого другого вещества в реакциях обмена. Например, при взаимодействии металлического цинка с кислотой один атом цинка вытесняет два атома водорода, отдавая при этом два электрона:

Zn + 2H⁺ = Zn²⁺ + H₂­

Zn⁰ - 2e^- = Zn²⁺

Следовательно, эквивалентом цинка является 1/2 его атома, т.е. 1/2 Zn (условная частица).

Число, показывающее, какая часть молекулы или формульной единицы вещества является его эквивалентом, называется фактором эквивалентности - f_э. Эквивалентная масса, или молярная масса эквивалента, определяется как произведение фактора эквивалентности на молярную массу:

Э = М·f_э

Например, в реакции полной нейтрализации серная кислота отдает два катиона водорода:

H₂SO₄ + 2KOH = K₂SO₄ + 2H₂O

Соответственно, эквивалентом серной кислоты является 1/2 H₂SO₄, фактор эквивалентности равен 1/2, а эквивалентная масса составляет (1/2)×98 = 49 г/моль. Гидроксид калия связывает один катион водорода, поэтому его эквивалентом является формульная единица, фактор эквивалентности равен единице, а эквивалентная масса равна молярной массе, т.е. 56 г/моль.

Из рассмотренных примеров видно, что при расчете эквивалентной массы необходимо определить фактор эквивалентности. Для этого существует ряд правил:

1. Фактор эквивалентности кислоты или основания равен 1/n, где n - число задействованных в реакции катионов водорода или гидроксид-анионов.

2. Фактор эквивалентности соли равен частному от деления единицы на произведение валентности (v) катиона металла или кислотного остатка и их числа (n) в составе соли (стехиометрический индекс в формуле):

f_э =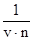

Например, для Al₂(SO₄)₃ f_э = 1/6.

Фактор эквивалентности оксида рассчитывается по аналогичной формуле, где v и n – валентность и число атомов кислорода, т.е. f_э = 1/2n.

3. Фактор эквивалентности окислителя (восстановителя) равен частному от деления единицы на число присоединенных (отданных) им электронов.

Следует обратить внимание на то обстоятельство, что одно и то же соединение может иметь разный фактор эквивалентности в разных реакциях. Например, в реакциях кислотно-основного взаимодействия:

H₃PO₄ + KOH = KH₂PO₄ + H₂O; f_э(H₃PO₄) = 1

H₃PO₄ + 2KOH = K₂HPO₄ + 2H₂O; f_э(H₃PO₄) = 1/2

H₃PO₄ + 3KOH = K₃PO₄ + 3H₂O; f_э(H₃PO₄) = 1/3

или в окислительно-восстановительных реакциях:

KMn⁺⁷O₄ + NaNO₂ + H₂SO₄ ® Mn⁺²SO₄ + NaNO₃ + K₂SO₄ + H₂O;

Mn⁺⁷ + 5e^- ® Mn⁺²; f_э(KMnO₄) = 1/5

KMn⁺⁷O₄ + NaNO₂ + H₂O ® Mn⁺⁴O₂ + NaNO₃ + KOH;

Mn⁺⁷ + 3e^- ® Mn⁺⁴; f_э(KMnO₄) = 1/3

Закон объемных отношений (Ж. Гей-Люссак, 1808 г.). Изучая реакции между газообразными веществами, Гей-Люссак обнаружил общую закономерность, присущую данным процессам. При постоянных температуре и давлении объемы вступивших в реакцию газов относятся друг к другу и к объемам газообразных продуктов реакции как небольшие целые числа.

Например, при синтезе аммиака из трех объемов водорода и одного объема азота образуются два объема аммиака.

N₂ + 3H₂ = 2NH₃

1V 3V 2V

Закон объемных отношений может быть объяснен на основе закона Авогадро.

Закон Авогадро (А. Авогадро, 1811 г.). Итальянский химик А. Авогадро показал, что закономерности реакций между газами могут быть объяснены, если принять следующее: в равных объемах различных газов при одинаковых температуре и давлении содержится одинаковое число молекул.

Закон Авогадро объясняется тем, что объем газа фактически представляет собой объем межмолекулярного пространства, тогда как собственным объемом молекул газа и силами притяжения между ними можно пренебречь. В результате объем газообразного вещества определяется лишь температурой и давлением и не зависит от природы, размеров и свойств молекул газа.

Из закона Авогадро вытекает несколько важных следствий:

1. При одинаковых условиях (температуре и давлении) один моль любого газа занимает одинаковый объем. При нормальных условиях (р₀ = 101,325 кПа, Т₀ = 273 К) молярный объем газа (V_m) составляет 22,414 л.

2. Объемы прореагировавших газов относятся друг к другу и к объемам газообразных продуктов реакции как коэффициенты в уравнениях реакций. Тем самым закон Авогадро объясняет закон объемных отношений.

3. В равных объемах различных газов при одинаковых условиях содержится равное количество вещества.

1.3. Методы определения молекулярных масс газообразных веществ

Метод измерения относительной плотности газа по газу. Относительной плотностью газа по газу называется отношение масс равных объемов газов, взятых при одинаковой температуре и давлении. Пусть m_A и m_B – массы равных объемов газов А и В. Тогда плотность газа А по газу В будет определяться следующим соотношением:

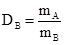
Поскольку m_A = n_A×M_A, а m_B = n_B×M_B, то

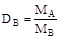или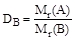

Следовательно, M_r(A) = M_r(B)×D_B

Относительная плотность может быть измерена по любому газу. Hа практике её часто определяют по водороду или воздуху. Соответственно, молекулярная масса может быть определена следующим образом:

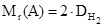или M_r(A) = 29×D_возд,

где 29 – средняя молекулярная масса воздуха.

Рассмотренный метод может быть применен и для определения молекулярных масс паров жидкостей.

Определение молекулярных масс по уравнению состояния идеального газа. Уравнение состояния идеального газа (уравнение Менделеева–Клапейрона) имеет следующий вид:

;

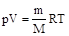где m - масса газа (кг), М – его молярная масса (кг/моль), р – давление (Па), V – объем (м³), Т – абсолютная температура (К), R – универсальная газовая постоянная (8,314 Дж/моль×К).

При не слишком низких температурах и невысоких давлениях реальные газы удовлетворительно следуют данному уравнению, и его можно использовать для определения молярных, а следовательно, и молекулярных масс газов. Для этого достаточно измерить температуру, давление, объем и массу газа, а затем рассчитать М по формуле:

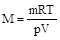
1.4. Методы определения атомных масс

Метод Канниццаро пригоден для определения атомных масс элементов, образующих соединения с молекулярной структурой (т.е. преимущественно для неметаллов). Согласно методу вначале определяют молекулярные массы для возможно большего числа соединений исследуемого элемента. Затем определяют содержание этого элемента в соединениях и расчитывают его массовую долю (w). Массу всех атомов элемента в молекуле определяют по формуле:

n·A_r = M_r·w

За атомную массу принимается наименьшее из значений n×A_r, так как в молекуле не может меньше одного атома данного элемента. В табл. 1 приведены результаты определения атомной массы углерода по методу Канниццаро. Из данных видно, что A_r(C) следует принять равной 12.

Таблица 1.

Определение атомной массы углерода по Канниццаро

Соединение	w(С), %	Mr	n×Ar
Углекислый газ	27,3
Угарный газ	42,9
Циановодород	44,4
Метан	75,0
Этан	80,0
Бензол	92,3

Метод Дюлонга-Пти основан на измерении молярных теплоемкостей простых веществ. Молярная теплоемкость простого вещества – это количество теплоты, необходимое для нагревания моля соответствующего элемента на 1 К.

С_М = С×М,

где С – удельная теплоемкость, М – молярная масса элемента. Исследуя атомные теплоемкости, П. Дюлонг и А. Пти установили закономерность, названную правилом Дюлонга-Пти (1819 г.): молярная теплоемкость простых веществ - величина постоянная. Правило подтверждают данные, приведенные в табл. 2. В среднем значения теплоемкостей близки к 25 кДж/моль×К.

Таблица 2.

Молярные теплоемкости некоторых простых веществ

Вещество	М, г/моль	C, Дж/г×К	СМ, Дж/моль×К
Литий	6,94	3,58	24,85
Алюминий	26,98	0,903	24,35
a-Сера	32,06	0,705	22,61
Железо	56,84	0,440	25,00
Селен	78,96	0,320	25,3
Молибден	95,94	0,251	24,1
Ртуть	200,59	0,140	27,99
Свинец	207,2	0,128	26,44

Приведенное выше уравнение позволяет определить приблизительное значение молярной массы элемента, если известна удельная теплоемкость вещества:

М¢ = =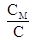

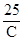
Чтобы уточнить найденное значение М', его следует сопоставить с эквивалентной массой элемента. Последняя либо равна молярной массе элемента, либо в целое число раз меньше ее.

В качестве примера определим атомную массу алюминия, для которого С = 0,903 Дж/г×К:

М¢ = 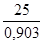= 27,68 (г/моль)

Зная, что эквивалентная масса алюминия равна 8,99 г/моль, найдем частное от деления М' на М_Э(Al) и округлим полученную величину (валентность) до целого числа

n = 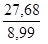= 3,08 » 3

Тогда, уточненная молярная масса алюминия составит:

M(Al) = М_Э(Al)×n = 8,99×3 = 26,97 (г/моль)

Соответственно, атомная масса алюминия равна 26,97.

СТРОЕНИЕ АТОМА