Свойства растворов высокомолекулярных веществ

Растворы ВМВобладают рядом своеобразных черт, обусловленных специфическими свойствами макромолекул и, глазным образом, их размерами. Некоторые макромолекулы линейных полимеров могут достигать в длину 100 - 1000 нм (10^-7 ¸ 10^-6 м), то есть их размеры соизмеримы с размерами частиц в ультрамикрогетерогенных дисперсных системах. Другая специфическая особенность макромолекул - способность принимать различные конформации, число которых достигает многих миллиардов. Причём каждая макромолекула в результате теплового движения непрерывно изменяет свою конформации, т. е. отдельные сегменты её совершают так называемое микроброуновское движение. Эти свойства макромолекул придают растворам ВМВ с одной стороны сходство с истинными растворами низкомолекулярных веществ, с другой - сходство с коллоидными растворами, с третьей - специфические черты, свойственные только им.

Свойства растворов ВМВ, сближающие их с истинными растворами низкомолекулярных веществ, обусловлены тем, что полимеры существуют в растворе в виде отдельных макромолекул. Макромолекулы, как правило, хорошо сольватированы, что даёт возможность называть такие растворы лиофильными коллоидами. Вот главные из таких свойств:

- растворы ВМВ образуются самопроизвольно;

- они термодинамически устойчивы;

- растворы ВМВ обратимы, т. е. могут быть многократно подвергнуты разделению на растворитель и полимер и последующему повторному растворению.

Большие размеры макромолекул придают растворам ВМВ свойства, сближающие их с коллоидными растворами:

- опалесценция;

- малое осмотическое давление;

- малая скорость диффузии;

- способность к электрофорезу.

Вместе с тем растворы полимеров обладают и рядом свойств, присущих только им (в принципе некоторые из этих свойств могут наблюдаться и у других систем, но там они являются скорее исключением, чем правилом):

- большая вязкость;

- способность к застудневанию;

- способность к высаливанию;

- коацервация;

- выделение из водных растворов под действием органических жидкостей.

Здесь более подробно будут рассмотрены именно эти специфические

свойства растворов высокомолекулярных веществ.

Вязкость. Вискозиметрия

Вязкостьили внутреннее трение - свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В данном разделе мы будем говорить только о вязкости жидкостей, преимущественно растворов полимеров.

Основной закон вязкого течения был установлен И. Ньютоном (1б87). Закон был выведен при рассмотрении движения двух плоскопараллельных пластинок (каждая с площадью внутренней поверхности, равной S) внутри вязкой жидкости (рис. 10.1).

Рис. 10.1. Распределение слоёв жидкости по скоростям при ламинарном

течении между неподвижной (нижней) и подвижной (верхней)

твёрдыми пластинками

Представим, что нижняя пластинка неподвижна, а верхняя сдвигается под действием силы F со скоростью. При этом слой жидкости, прилегающий к верхней пластинке, и связанный с ней силами адгезии, будет перемещаться вместе с пластинкой в том же направлении и с той же скоростью v. Слой жидкости, прилегающий к нижней пластинке, будет оставаться неподвижным. Все промежуточные слои жидкости будут перемещаться с различными скоростями, которые будут тем больше, чем ближе к подвижной пластинке находятся слои. При небольшом зазоре у между пластинками концы векторов скорости всех слоёв будут лежать на одной прямой линии.

В современной трактовке закон звучит так:

при ламинарном течении жидкости между двумя плоскопараллельными пластинками скорость течения слоя жидкости прямо пропорциональна напряжению сдвига и расстоянию от неподвижной пластинки.

Этому закону соответствует математическое выражение

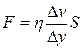или ,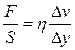

где F - касательная сила, вызывающая сдвиг слоёв жидкости относительно друг друга; S - площадь слоя, по которому происходит сдвиг; Dv /Dy - градиент скорости течения (быстрота изменения её от слоя к слою), иначе - скорость сдвига. Отношение F / S называется напряжением сдвига. Коэффициент пропорциональности h называется коэффициентом динамической вязкостиили просто динамической вязкостьюжидкости.

Жидкости, подчиняющиеся закону Ньютона – чистые жидкости (вода, органические жидкости, расплавленные металлы и т. п.), а также разбавленные растворы и коллоидные растворы, - называются ньютоновскими жидкостями. Соответственно, те жидкости, в которых не наблюдается линейной зависимости скорости течения от напряжения сдвига, называются неньютоновскими. К ним относятся дисперсные системы с большой концентрацией частиц дисперсной фазы – концентрированные суспензии, пасты, эмульсии, а также гели и студни.

Динамическая вязкость является основной количественной характеристикой вязкого течения жидкостей. В системе СИ единицей h является Па·c (паскаль-секунда). Для большинства чистых низкомолекулярных жидкостей и растворов на их основе h обычно не превышает 10 Па·c (для дистиллированной воды при 25 ^оС 0,001 Па·c). Растворы же высокомолекулярных веществ, а также сами расплавленные ВМВ обладают намного большей вязкостью.

Величина, обратная динамической вязкости, называется текучестью.

На практике вязкость ньютоновских жидкостей обычно определяют с помощью капиллярных вискозиметровтипа вискозиметра Оствальдаили Убеллоде, в которых определённый объём исследуемой жидкости под действием силы тяжести протекает через узкий длинный капилляр. В таком цилиндрическом капилляре при равномерной скорости течения устанавливается параболическое распределение скоростей слоёв (рис. 10.2).

Рис. 10.2. Распределение слоёв жидкости по скоростям при ламинарном

течении в узком капилляре

Такое распределение описывается законом Ж. Л. М. Пуазейля (1840 - 41):

объёмная скорость течения жидкости по цилиндрическому капилляру малого сечения прямо пропорциональна перепаду давления на концах капилляра и четвёртой степени его радиуса и обратно пропорциональна длине капилляра.

Закон может быть выражен уравнением (уравнение Пуазейля – Гагена):

,

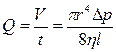где Q - объёмная скорость течения, равная отношению объёма жидкости V ко времени t его протекания по капилляру с радиусом r и длиной l; Dp - разность давлений на концах капилляра, вызывающая течение жидкости.

Так как скорость вытекания жидкости из сосуда по вертикальному капилляру зависит от её плотности, следует сделать на это поправку. Обычно это выражается в том, что наряду с динамической вязкостью жидкости характеризуют ещё и так называемой кинематической вязкостьюh_кин:

,

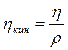где r- плотность жидкости.

Кинематическая вязкость измеряется в м²/с.

Идентичность коэффициента динамической вязкости в уравнениях Ньютона и Пуазейля была доказана Дж. Стоксом. Им же был предложен ещё один простой метод определения динамической вязкости - метод падающего шарика, при котором плотный шарик из инертного материала свободно падает в вязкой среде. Вязкость определяется по скорости прохождения падающим шариком промежутков между метками на сосуде, например, мерном цилиндре с жидкостью. Её расчёт основан на уравнении Стокса, приведённому в п. 7.3.

На практике обычно определяют не собственно динамическую вязкость, что связано с трудностями точного измерения параметров вискозиметров - размеров капилляра, перепада давления, радиуса шарика и т. д.), а так называемую относительную вязкостьh_отн:

,

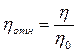где h - динамическая вязкость исследуемой жидкости; h₀ - вязкость эталонной жидкости (обычно за эталон принимается вода, но в случае работы неводными растворами можно принять чистый растворитель).

Так как по закону Пуазейля вязкость жидкости прямо пропорциональна времени её истечения из капилляра, то в расчётную формулу для относительной вязкости входит отношение времени истечения исследуемой жидкости t и эталонной t₀ (при одинаковой или почти одинаковой плотности):

.

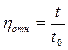При исследовании растворов чаще всего требуется установить зависимость вязкости раствора от его концентрации. Для этих целей удобно пользоваться удельной вязкостьюh_уд, характеризующей прирост вязкости раствора h по сравнению с вязкостью растворителя h₀:

.

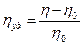Г. Штаудингером было показано, что для разбавленных растворов линейных полимеров с относительно короткими и жёсткими макромолекулами (например, целлюлоза), удельная вязкость пропорциональна их молярной массе М и массо-объёмной концентрации С:

,

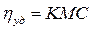где К - константа, характерная для данного полимергомологического ряда и растворителя.

Из этого уравнения следует, что удельная вязкость, отнесённая к единице концентрации (приведённая вязкость), не зависит от концентрации раствора полимера и пропорциональна его молекулярной массе:

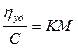
Полученное уравнение (уравнение Штаудингера)можно использовать для определения молярной массы полимеров. Константа К при этом определяется каким-либо независимым методом.

Уравнение Штаудингера, как уже говорилось выше, применимо только для растворов полимеров с достаточно жёсткими макромолекулами. Гибкие длинные макромолекулы обычно сворачиваются в клубки, что уменьшает сопротивление их движению. При этом изменяется константа К, а зависимость вязкости раствора полимера от молярной массы оказывается нелинейной. В таких случаях более правильно связывать с молекулярной массой полимера характеристическую вязкость[h], так как именно этой величиной оценивается прирост вязкости растворов, вызванный особенностями конформацийи микроброуновского движениямакромолекул. Характеристическая вязкость представляет собой предел, к которому стремится удельная вязкость раствора ВМВ при бесконечно малой концентрации:

.

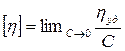Как правило, [h] определяется графическим способом при построении зависимости приведённой вязкости раствора полимера от его массо-объ­ём­ной концентрации как отрезок, отсекаемый этой линией от оси h_уд/С (рис. 10.3).

Рис. 10.3. Зависимость приведённой вязкости раствора полимера

от его массо-объ­ём­ной концентрации

Существует уравнение Марка – Хаувинка - Кунадля вычисления мо­лярной массы полимеров, включающее в себя приведённую вязкость:

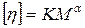
где К и a - постоянные для данного полимергомологического ряда и растворителя. Константа a, отражающая форму и плотность клубка макромолекулы, зависит от природы растворителя. Её значения лежат в основном в пределах от 0,5 до 1,0.

Следует помнить, что вычисленная таким образом молярная масса исследуемого полимера является средней, поскольку, как правило, в одном и том же образце полимера, в особенности синтетического, может присутствовать множество фракций, содержащих макромолекулы разной длины. Это же относится и к другим методам определения молярной массы ВМВ.