Окружающая среда – это все, что находится за пределами системы.

Система характеризуется определенными термодинамическими параметрами (свойствами)(температура, давление, объём, масса, концентрация и др.).

В химической термодинамике используется абсолютная шкала температур, единицей измерения в которой является кельвин (К). Сохранила значение также шкала Цельсия (единица измерения – градус Цельсия, ^оС). Нуль по шкале Цельсия равен 273,15 К.

В качестве единицы давления в Международной системе (СИ) используют паскаль (Па). Нередко используют также миллиметр ртутного столба (мм рт. ст.) и атмосферу (атм), 1 атм=760 мм рт. ст.=101325 Па =101,325 кПа.

За стандартные условияпринимают температуру 298,15 К (25 ^оС) и давление 101,325 кПа. Иногда используют нормальные условия(Т=273,15 К, или 0^оС, и р=101,325 кПа=1 атм=760 мм рт.ст.).

Термодинамика рассматривает равновесныесостояния системы, т.е. случай, когда термодинамические параметры одинаковы во всех точках системы.

Термодинамика изучает переходы системы из одного состояния в другое. Если переходы происходят при постоянстве некоторых параметров, то они называются:

1) изобарными (р=const);

2) изохорными (V=const);

3) изотермическими (T=const);

4) изобарно-изотермическими(р=const, T=const) и т.д.

Состояние системы описывают термодинамическими функциями состояния системы,или характеристическими функциями. Особенностью термодинамических функций состояния является независимость изменения функции от пути процесса. Их значение определяется только состоянием системы, т.е. параметрами системы (р, Т и др.).

Термодинамические параметры, не зависящие от количества (или массы) вещества, называют интенсивными(р, Т), а зависящие –экстенсивными. Функции состояния являются экстенсивными параметрами, поэтому их относят к 1 моль вещества. Наиболее используемыми являются следующие функции состояния: внутренняя энергия U, энтальпия H, энтропия S и энергия Гиббса G.

Первый закон (начало) термодинамики. Любой процесс подчиняется закону сохранения энергии, выражаемому уравнением

Q = ΔU + W. (3.1)

Уравнение (3.1) означает, что теплота Q, сообщенная системе, расходуется на изменение внутренней энергии системы ΔU и выполнение работы W против внешних сил.

Под внутренней энергией понимают общий запас энергии системы за исключением потенциальной энергии положения системы и кинетической энергии движения системы как целого. Внутренняя энергия представляет собой способность системы к совершению работы или передаче теплоты. Определить абсолютное значение внутренней энергии системы невозможно т.к., с одной стороны, это означало бы возможность состояния системы с энергией равной нулю, а с другой стороны, современной науке известны не все формы энергии. Тем не менее, можно найти изменение внутренней энергии системы при переходе из одного состояния в другое:

ΔU = U₂ – U₁. (3.2)

Теплота Q представляет собой меру хаотического движения частиц данной системы. Теплота передается от более нагретого тела к менее нагретому телу.

Работа W является мерой энергии, передаваемой от одной системы к другой под действием тех или иных сил.

Теплота и работа не являются функциями состояния, т.е. они зависят от пути процесса.

Единицей измерения теплоты и работы является джо- уль (Дж). Теплота, подводимая к системе, считается положительной (Q>0), а теплота выделяемая системой, – отрицательной (Q<0).

Формула (3.1) является математическим выражением первого закона термодинамики: энергия не возникает и не исчезает, но лишь переходит из одной формы в другую.

Энтальпия. Работа, производимая системой, может быть разделена на работу против внешнего давления рΔV и работу против всех прочих сил W′:

W = W′ + рΔV,

где р – внешнее давление; ΔV – изменение объема ( ΔV=V₂ – V₁ ; V₂ – объем системы в конечном состоянии или объем продуктов реакции; V₁ – объем системы в начальном состоянии или объем исходных веществ).

Если из всех внешних сил на систему действует только постоянное давление (р=const; изобарный процесс), то уравнение (3.1) запишется следующим образом:

Q_p=ΔU+рΔV=U₂–U₁+pV₂– pV₁=(U₂ +pV₂)– (U₁ + pV₁). (3.3)

Сумму

U+pV=H (3.4)

называют энтальпией. Энтальпия является термодинамическим свойством, так же как масса, объем и т.д. Одновременно энтальпия – функция состояния системы, т.е. ее изменение не зависит от пути процесса, а определяется только состоянием системы в конце и начале процесса. Энтальпия является экстенсивным свойством, т.е. ее численное значение пропорционально количеству вещества. Единицей измерения энтальпии является джоуль на моль (Дж/моль).

Подставив уравнение (3.3) в (3.4), получим уравнение

Q_p=H₂–H₁=ΔH. (3.5)

Из уравнения (3.5) следует, что энтальпия – это теплота, выделяемая или поглощаемая в ходе изобарного процесса (тепловой эффект изобарного процесса равен изменению энтальпии в ходе этого процесса).

Если понимать под Н₂ энтальпии всех конечных продуктов реакции (ΣΗ_f), а под H₁ – энтальпии всех исходных веществ (ΣΗ_i), то уравнение (3.5) для химической реакции запишется следующим образом:

Q_p = Δ_rH= ΣΗ_f - ΣΗ_i, (3.6)

где Δ_rH – изменение энтальпии в ходе химической реакции, или энтальпия реакции.

Для изохорного процесса (V=const, ΔV=0) уравнение (3.2) примет вид

Q_v = ΔU = U₂ – U₁, (3.7)

т.е. тепловой эффект изохорного процесса равен изменению внутренней энергии системы.

Для химической реакции, протекающей при постоянном объёме, уравнение (3.7) по аналогии с (3.6) можно записать так:

Q_v = Δ_rU= ΣU_f - ΣU_i . (3.8)

Химические процессы, протекающие с выделением теплоты, называются экзотермическими(ΔU<0; ΔH<0), а с поглощением теплоты – эндотермическими(ΔU>0; ΔH>0).

Химические уравнения, для которых указаны тепловые эффекты, называются термохимическими уравнениями. В термохимических уравнениях обычно указывают также агрегатное состояние веществ, концентрации растворов и другие факторы, влияющие на величину теплового эффекта реакции. Для того чтобы отнести тепловой эффект к 1 моль какого-либо вещества, в термохимических уравнениях иногда используют дробные стехиометрические коэффициенты. Приведем несколько примеров термохимических уравнений:

Н_2(г) + 1/2О_2(г) = Н₂О_(ж), 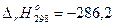кДж;

Н_2(г) + 1/2О_2(г) = Н₂О_(г), 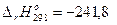кДж;

С_(гр) + О_2(г) = СО_2(г), 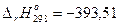кДж;

С_(алм) + О_2(г) = СО_2(г), 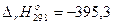кДж,

где г – газ; ж – жидкость; гр – графит; алм – алмаз.

В выражении 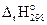индексы имеют следующее значение: 1) r означает, что изменение энтальпии относится к химической реакции; 2) правый нижний индекс (298) означает температуру системы; 3) правый верхний индекс (о) указывает на стандартное состояние веществ, участвующих в реакции. За стандартное состояние твердых веществ принимают состояние чистого кристаллического вещества, находящегося при стандартных условиях (298 К, 101,325 кПа) в виде стабильной в этих условиях модификации. Стандартное состояние жидких веществ – чистая жидкость, а газообразных – чистый газ при стандартных условиях.

Закон Гесса. Открыт в 1840 г. российским ученым Г.И. Гессом. Тепловой эффект реакции, протекающей при постоянном давлении или постоянном объеме, не зависит от пути протекания реакции и определяется только природой и состоянием исходных веществ и конечных продуктов.

Рассмотрим процесс получения оксида углерода (IV) из графита:

С_(гр) + О_2(г) = СО_2(г) .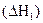

Эту же реакцию можно осуществить в две стадии через образование оксида углерода (II):

С_(гр) + 1/2О_2(г) = СО_(г)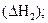

СО_(г) + 1/2 О_2(г) = СО_2(г)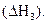

Эти реакции можно представить следующей схемой:

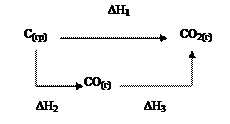
В соответствии с законом Гесса можно записать:

ΔН₁ = ΔН₂ + ΔН₃ или ΔН₁ - ΔН₂ - ΔН₃ = 0. (3.9)

Процессы, в которых система после ряда последовательных превращений возвращается в исходное состояние, называются круговыми процессами или термодинамическими циклами. Метод циклов используется для вычисления различных термодинамических свойств веществ. Так, в рассматриваемом цикле ΔН₁ и ΔН₃ могут быть относительно легко определены экспериментально, и затем из уравнения (3.9) можно найти величину ΔН₂, которую по объективным причинам сложно измерить:

ΔН₂ = ΔН₁ - ΔН₃.

Закон Гесса имеет ряд следствий. Рассмотрим два из них.

Первое следствие закона Гесса. Энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ.

Энтальпия образования вещества В ( 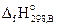) – это энтальпия реакции образования 1 моль соединения из простых веществ, устойчивых при стандартных условиях.Например, энтальпия образования нитрата натрия равна энтальпии реакции

Na_(кр) + ½N_2(г) + 3/2О_2(г) = NaNO_3(кр)

и составляет 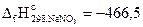кДж/моль.

Энтальпия образования простых веществ при стандартных условиях принята равной нулю. Стандартные энтальпии образования большого количества химических соединений определены экспериментально и приводятся в справочных изданиях.

Энтальпия химической реакции в общем виде

аА + bB = dD + eE (3.10)

определяется по уравнению

.

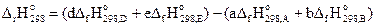(3.11)

Пример 3.1.Рассчитать стандартную энтальпию реакции

Al₂(SO₄)_3(т) = Al₂O_3(т) + 3SO_3(г), если стандартные энтальпии образования кристаллических сульфата алюминия и оксида алюминия и газообразного оксида серы (VI) составляют -3441; -1675 и -396 кДж/моль соответственно.

Решение. Из первого следствия закона Гесса

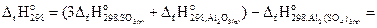=[3(-396) +(-1675)] – (-3441)= 578 кДж.

Пример 3.2. Реакция горения этана выражается термохимическим уравнением

С₂Н_6(г) + 3,5 О_2(г) = 2СО_2(г) + 3Н₂О_(ж) , Δ_rН^o = -1559, 87 кДж.

Вычислить энтальпию образования этана, если стандартные энтальпии образования СО_2(г) и Н₂О_(ж) составляют -393,51 и -237,19 кДж/моль соответственно.

Решение. На основании первого следствия из закона Гесса можно записать:

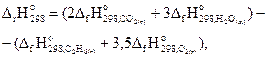
откуда

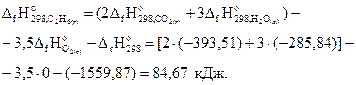
Пример 3.3.Вычислить количество теплоты, которое выделяется при окислении 20 г сульфида цинка кислородом.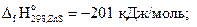

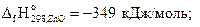
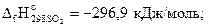
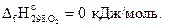
Решение. Из уравнения реакции

2ZnS + 3O₂ = 2ZnO + 2SO₂

на основании первого следствия из закона Гесса можно записать:

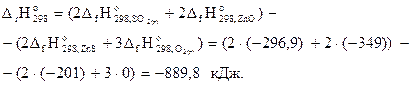
Это количество энергии (889,8 кДж) выделяется при окислении 2 моль сульфида цинка, т.е. 2(65+32)=194 г. Составим пропорцию:

при окислении 194 г ZnS выделяется (-889,8 кДж),

- “ - 20 г ZnS - “ - х кДж),

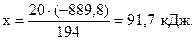
Пример 3.4.Определить 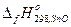исходя из следующих данных:

1) Sn_(бел) + О_2(газ) = SnO_2(кр) – 580,8 кДж;

2) 2SnО_(кр) + О_2(газ) = 2 SnO_2(кр) – 589,6 кДж.

Решение. Из уравнения (1) следует, что тепловой эффект этой реакции равен стандартной энтальпии образования SnO_2(кр)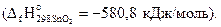

Запишем выражение для теплового эффекта реакции (2), используя первое следствие закона Гесса:

.

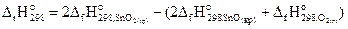Отсюда выразим стандартную энтальпию образования SnO_(кр):

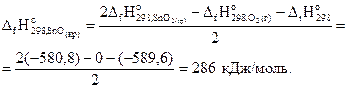
Второе следствие закона Гесса. Энтальпия химической реакции равна сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции.

Энтальпия сгорания вещества В ( 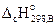) – это энтальпия реакции окисления кислородом 1 моль соединения до образования высших оксидов.Например, энтальпия реакции сгорания метанола есть изменение энтальпии следующей реакции:

СН₃ОН + 3/2О₂ = СО₂ + 2Н₂О.

Стандартные энтальпии сгорания большого количества органических соединений определены экспериментально и приводятся в справочных изданиях.

Энтальпия химической реакции в общем виде (3.10) определяется по уравнению

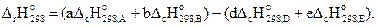
(3.12)

Уравнение (3.12) имеет особое значение для органических веществ.

Пример 3.5.Рассчитать стандартную энтальпию реакции

C₂H_4(г) + Н_2(г) = С₂Н_6(г) , если стандартные энтальпии сгорания газообразных этана и этилена составляют -1559,88 и -1410,97 кДж/моль соответственно.

Решение. На основании второго следствия закона Гесса запишем:

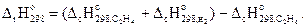
Стандартная энтальпия сгорания водорода равна стандартной энтальпии образования воды, т.е.

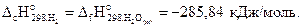
Подставляя численные значения величин в выражение для стандартной энтальпии реакции, получим

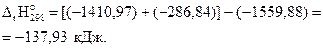
Пример 3.6.Рассчитать стандартную энтальпию реакции образования As₂O₅, используя следующие данные:

1) 4As_(кр)+3О_2(г)=2As₂O_3(кр) – 1313,6 кДж;

2) As₂O_3(кр)+О_2(г)= As₂O_5(кр) – 311,2 кДж.

Решение: Из уравнения (1) в соответствии с определением энтальпии образования вещества следует, что 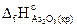составляет половину теплового эффекта этой реакции, т.е. (-1213,6/2)=-606,8 кДж/моль.

Для уравнения (2) на основании 1-го следствия закона Гесса запишем:

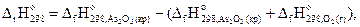
откуда

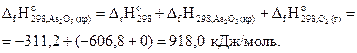
Энтропия. Энергия Гиббса

Одним из важнейших вопросов химии является вопрос о возможности протекания химической реакции. Количественным критерием принципиальной осуществимости химической реакции является, в частности, характеристическая функция состояния системы, называемая энергией Гиббса (G). Прежде чем перейти к рассмотрению этого критерия, остановимся на ряде определений.

Самопроизвольные процессы. Самопроизвольными называют процессы, происходящие без подвода энергии от внешнего источника. Многие химические процессы являются самопроизвольными, например растворение сахара в воде, окисление металлов на воздухе (коррозия) и др.

Обратимые и необратимые процессы. Многие химические реакции протекают в одном направлении до полного исчерпания реагирующих веществ. Такие реакции называются химически необратимыми. В качестве примера можно привести взаимодействие натрия и воды.

Другие реакции протекают вначале в прямом направлении, а затем в прямом и обратном благодаря взаимодействию продуктов реакции. В результате образуется смесь, содержащая одновременно исходные вещества и продукты реакции. Такие реакции называют химически обратимыми.В результате химически обратимого процесса наступает истинное (устойчивое) химическое равновесие, которое характеризуется следующими признаками:

1) в отсутствие внешних воздействий состояние системы остается неизменным неограниченно долго;

2) любое изменение внешних условий приводит к изменению состояния системы;

3) состояние равновесия не зависит от того, с какой стороны оно достигнуто.

В качестве примера системы, находящейся в состоянии истинного равновесия, можно привести эквимолекулярную смесь

СО_(г) + Н₂О_(г) 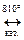СО_2(г) + Н_{2 (г)}.

Любое изменение температуры или других условий вызывает смещение равновесия, т.е. изменение состава системы.

Кроме истинных равновесий очень часто встречаются кажущиеся (ложные, заторможенные) равновесия, когда состояние системы сохраняется во времени очень долго, но небольшое воздействие на систему может привести к сильному изменению ее состояния. Примером может быть смесь водорода и кислорода, которая при комнатной температуре в отсутствие внешних воздействий может оставаться неизменной неограниченно долго. Однако достаточно ввести в эту смесь платинированный асбест (катализатор), как начнется энергичная реакция

Н_2(г) + О_2(г) = Н₂О­_(ж),

ведущая к полному исчерпанию исходных веществ.

Если ввести тот же катализатор при тех же условиях в жидкую воду, то получить исходную смесь невозможно.

Энтропия. Состояние любой системы может быть охарактеризовано значениями непосредственно измеряемых параметров (р, Т и др.). Это характеристика макросостояния системы. Состояние системы может быть описано также характеристиками каждой частицы системы (атома, молекулы): координатой, частотой колебания, частотой вращения и т.д. Это характеристика микросостояния системы. Системы состоят из очень большого числа частиц, поэтому одному макросостоянию будет отвечать огромное число различных микросостояний. Это число называется термодинамической вероятностью состояния и обозначается как W.

Термодинамическая вероятность связана с другим свойством вещества – энтропией (S, Дж/(моль^.К)) –формулой Больцмана

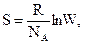(3.13)

где R − универсальная газовая постоянная, а N_A – постоянная Авогадро.

Физический смысл энтропии может быть пояснен следующим мысленным экспериментом. Пусть идеальный кристалл какого-либо вещества, например хлорида натрия, охлажден до абсолютного нуля температуры. В этих условиях ионы натрия и хлора, составляющие кристалл, становятся практически неподвижными, и данное макроскопическое состояние характеризуется одним единственным микросостоянием, т.е. W=1, и в соответствии с (3.13) S=0. При повышении температуры ионы начнут колебаться около положений равновесия в кристаллической решетке, число микросостояний, соответствующих одному макросостоянию, возрастает, и, следовательно, S>0.

Таким образом, энтропия является мерой неупорядоченности состояния системы. Энтропия системы увеличивается во всех процессах, сопровождающихся уменьшением упорядоченности (нагревание, растворение, испарение, реакции разложения и т.п.). Процессы, идущие с увеличением упорядоченности (охлаждение, кристаллизация, сжатие и т.п.), приводят к уменьшению энтропии.

Энтропия является функцией состояния, но в отличие от большинства других термодинамических функций возможно экспериментальное определение абсолютного значения энтропии вещества. Эта возможность основана на постулате М. Планка, согласно которому при абсолютном нуле энтропия идеального кристалла равна нулю(третий закон термодинамики).

Температурная зависимость энтропии вещества представлена качественно на рис. 3.1.

На рис. 3.1 видно, что при температуре, равной 0 К, энтропия вещества равна нулю. При повышении температуры энтропия плавно увеличивается, а в точках фазовых переходов имеет место скачкообразное увеличение энтропии, определяемое соотношением

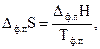(3.14)

где Δ _ф.пS, Δ_ф.пН и Т_ф.п − изменения энтропии, энтальпии и температура фазового перехода соответственно.

Энтропию вещества B в стандартном состоянии обозначают как 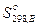. Для многих веществ абсолютные значения стандартных энтропий определены и приводятся в справочных изданиях.

Энтропия, так же как внутренняя энергия и энтальпия, является функцией состояния, поэтому изменение энтропии системы в процессе не зависит от его пути и определяется только начальным и конечным состояниями системы. Изменение энтропии в ходе химической реакции (3.10) может быть найдено как разность суммы энтропий продуктов реакции и суммы энтропий исходных веществ:

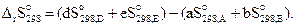(3.15)

Понятие энтропии используется в одной из формулировок второго закона термодинамики: в изолированных системах могут самопроизвольно протекать только процессы, идущие с увеличением энтропии (ΔS>0).Под изолированными системами понимаются системы, не обменивающиеся с окружающей средой ни веществом, ни энергией. Системы, в которых протекают химические процессы, к изолированным системам не относятся, т.к. они обмениваются с окружающей средой энергией (тепловой эффект реакции) и в таких системах могут протекать процессы и с уменьшением энтропии.

Пример 3.7.Рассчитать стандартную энтропию реакции

SO_2(г) + 2H₂S_(г) = 3S_(т) + 2Н₂О_(ж), если стандартные энтропии оксида серы (IV), сероводорода, серы и воды составляют 248,1; 205,64; 31,88 и 69,96 Дж/(моль• К) соответственно.

Решение. На основании уравнения (3.15) можно записать:

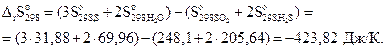
Энтропия в данной реакции уменьшается, что связано с образованием твердого и жидкого продуктов из газообразных веществ.

Пример 3.8.Не производя вычислений, определить знак изменения энтропии в следующих реакциях:

1) NH₄NO_3(к) = N₂O_(г) + 2Н₂О_(г),

2) 2Н_2(г) + О_2(г) = 2Н₂О_(г),

3) 2Н_2(г) + О_{2(г) =} 2Н₂О_(ж).

Решение. В реакции (1) 1 моль NH₄NO₃ в кристаллическом состоянии образует 3 моль газов, следовательно, D_rS₁>0.

В реакциях (2) и (3) уменьшается как общее число молей, так и число молей газообразных веществ. Следовательно, D_rS₂ <0 и D_rS₃<0. При этом уменьшение энтропии в реакции (3) больше, чем в реакции (2) , так как S^о(H₂O _(ж)) < S^о(H₂O_(г)).

Энергия Гиббса (изобарно-изотермический потенциал). Во многих случаях самопроизвольные процессы в природе протекают при наличии разности потенциалов, например, разность электрических потенциалов обусловливает перенос заряда, а разность гравитационных потенциалов – падение тела. Эти процессы заканчиваются при достижении минимума потенциала. Движущей силой химических процессов, протекающих при постоянных давлении и температуре, является изобарно-изотермический потенциал, называемый энергией Гиббсаи обозначаемый G. Изменение энергии Гиббса в химическом процессе определяется соотношением

ΔG = ΔH –TΔS, (3.16)

где ΔG – изменение энергии Гиббса химического процесса; ΔH – изменение энтальпии химического процесса; ΔS – изменение энтропии химического процесса; Т – температура, К.

Уравнение (3.16) может быть представлено в следующем виде:

ΔH = ΔG + TΔS. (3.17)

Смысл уравнения (3.17) в том, что часть теплового эффекта реакции расходуется на совершение работы (ΔG), а часть рассеивается в окружающую среду (TΔS).

Энергия Гиббса является критерием принципиальной возможности самопроизвольного протекания реакции. Если в ходе реакции энергия Гиббса уменьшается, то процесс может протекать в данных условиях самопроизвольно:

ΔG < 0. (3.18)

Процесс в данных условиях неосуществим, если

ΔG > 0. (3.19)

Выражения (3.18) и (3.19) одновременно означают, что обратная реакция не может (3.18) или может (3.19) протекать самопроизвольно.

Реакция является обратимой, т.е. может протекать и в прямом, и в обратном направлениях, если

ΔG = 0. (3.20)

Уравнение (3.20) является термодинамическим условием химического равновесия.

Соотношения (3.18) –(3.20) применимы также к фазовым равновесиям, т.е. к случаям, когда в равновесии находятся две фазы (агрегатных состояния) одного и того же вещества, например лед и жидкая вода.

Энтальпийный и энтропийный факторы. Из уравнений (3.16) и (3.18) следует, что процессы могут протекать самопроизвольно (ΔG<0), если они сопровождаются уменьшением энтальпии (ΔH<0) и увеличением энтропии системы (ΔS>0). Если же энтальпия системы увеличивается (ΔH>0), а энтропия уменьшается (ΔS<0), то такой процесс протекать не может (ΔG>0). При иных знаках ΔS и ΔН принципиальная возможность протекания процесса определяется соотношением энтальпийного (ΔH) и энтропийного (ТΔS) факторов.

Если ΔН>0 и ΔS>0, т.е. энтальпийная составляющая противодействует, а энтропийная благоприятствует протеканию процесса, то реакция может протекать самопроизвольно за счет энтропийной составляющей, при условии, что |ΔH|<|TΔS|.

Если энтальпийная составляющая благоприятствует, а энтропийная противодействует протеканию процесса, то реакция может протекать самопроизвольно за счет энтальпийной составлящей, при условии, что |ΔH|>|TΔS|.

Влияние температуры на направление реакции. Температура влияет на энтальпийную и энтропийную составляющие энергии Гиббса, что может сопровождаться изменением знака энергии Гиббса этих реакций, а следовательно, и направления протекания реакций. Для ориентировочной оценки температуры, при которой происходит смена знака энергии Гиббса, можно пренебречь зависимостью ΔН и ΔS от температуры. Тогда из уравнения (3.16) следует, что изменение знака энергии Гиббса произойдет при температуре

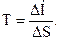(3.21)

Очевидно, что смена знака энергии Гиббса с изменением температуры возможна только в двух случаях: 1) ΔН>0 и ΔS>0 и 2) ΔН<0 и ΔS<0.

Стандартная энергия Гиббса образования 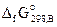– это изменение энергии Гиббса реакции образования 1 моль соединения из простых веществ, устойчивых при стандартных условиях.Энергия Гиббса образования простых веществ принимается равной нулю. Стандартные энергии Гиббса образования веществ можно найти в соответствующих справочниках.

Энергия Гиббса химической реакции. Энергия Гиббса является функцией состояния, т.е. ее изменение в процессе не зависит от пути его протекания, а определяется исходным и конечным состояниями системы. Следовательно, энергию Гиббса химической реакции (3.10) можно рассчитать по формуле

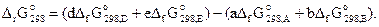
(3.22)

Отметим, что выводы о принципиальной возможности протекания реакции по величине Δ_rG применимы только к тем условиям, для которых вычислено изменение энергии Гиббса реакции. Если условия отличаются от стандартных, то для нахождения Δ_rG может быть использовано уравнение изотермы Вант-Гоффа, которое для реакции (3.10) между газами записывается как

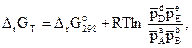(3.23)

а между растворенными веществами –

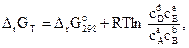(3.24)

где 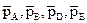– парциальные давления соответствующих веществ; с_А, с_В, с_D, c_E – концентрации соответствующих растворенных веществ; а, b, d, е – соответствующие стехиометрические коэффициенты.

Если реагирующие вещества находятся в стандартном состоянии, то уравнения (3.23) и (3.24) превращаются в уравнение

.

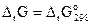Пример 3.9. Установить возможность протекания реакции NH_3(г) + HCl_(г) = NH₄Cl_(к)в стандартных условиях при температуре 298,15 К, используя данные по стандартным энтальпиям образования и энтропиям.

Функция	NH3(г)	HCl(г)	NH4Cl(к)
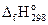, кДж/моль	-46,19	- 92,31	-315,59
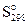, Дж/(моль•К)	192,5	186,68	94,5

Решение. На основании первого следствия закона Гесса найдём стандартную энтальпию реакции:

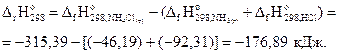
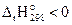; реакция экзотермическая, следовательно, энтальпийная составляющая благоприятствует протеканию реакции.

Изменение энтропии реакции рассчитаем по уравнению

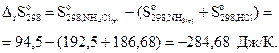
Реакция сопровождается уменьшением энтропии, значит, энтропийная составляющая противодействует протеканию реакции.

Найдём изменение энергии Гиббса процесса по уравнению (3.16):

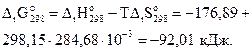
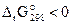, таким образом, данная реакция может протекать самопроизвольно при стандартных условиях.

Пример 3.10.Используя данные по стандартным энтальпиям образования и энтропиям, определить, при какой температуре наступит равновесие в системе N_2(г) + 3Н_2(г) = 2NH_3(г).

Функция	NH3(г)	H2(г)	N2(г)
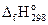, кДж/моль	-46,19
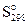, Дж/(моль•К)	192,5	130,6	191,5

Решение. Условием равновесия системы является ΔG=0. Для этого, используя соотношение (3.21), найдем температуру, при которой ΔG=0. Вычислим стандартные энтальпию и энтропию реакции:

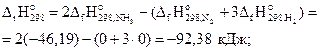
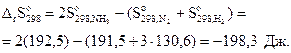
Энтальпийная составляющая благоприятствует, а энтропийная противодействует протеканию реакции, значит, при некоторой температуре возможна смена знака энергии Гиббса, т.е изменение направления протекания реакции.

Условие равновесия запишется следующим образом:

ΔG = ΔH –TΔS,

или, подставляя численные значения, получим

0 = - 92,38 – Т(-198,3) •10^-3.

Следовательно, реакция будет находиться в состоянии равновесия при температуре

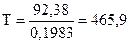К.

Ниже этой температуры реакция будет протекать в прямом направлении, а выше – в обратном.

Пример 3.11. При некоторой температуре Т эндотермическая реакция А® В практически идет до конца. Определить: а) знак D_rS реакции; б) знак DG реакции В ® А при температуре Т; в) возможность протекания реакции В ® А при низких температурах.

Решение. а) Самопроизвольное протекание реакции А ® В указывает, что DG<0. Поскольку DН>0, то из уравнения
DG = DH - TDS следует, что DS>0; для обратной реакции В ® А DS<0.

б) Для реакции А ® В DG<0. Следовательно, для обратной реакции при той же температуре DG>0.

в) Реакция А ® В эндотермическая (DH<0), следовательно, обратная реакция В ® А экзотермическая. При низких температурах абсолютная величина члена TDS мала, так что знак DG определяется знаком DН. Следовательно, при достаточно низких температурах протекание реакции В ® А возможно.

Пример 3.12. Рассчитать величину энергии Гиббса и определить, возможна ли реакция CO + Cl₂ ÛCOCl₂ при температуре 700 К, если константа равновесия реакции при этой температуре равна 10,83 атм^-1 и парциальные давления всех компонентов одинаковы и равны единице.

Решение. Взаимосвязь D_rG⁰ и К_р реакции А + В Û С + D дается уравнением изотермы (3.22)

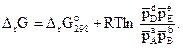
При стандартных условиях, когда парциальное давление каждого реагирующего вещества равно 1 атм, это соотношение примет вид

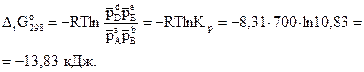
Следовательно, реакция при Т=700 К может протекать в прямом направлении самопроизвольно.

3.3. Вопросы и задачи для самостоятельной подготовки

1. Приведите численные значения давления и температуры в международной системе единиц, а также в атмосферах, миллиметрах ртутного столба и градусах Цельсия, соответствующие стандартным и нормальным условиям.

2. Какому условию удовлетворяют функции состояния? Что определяет изменение значения функции состояния в процессе?

3. Постоянством каких параметров характеризуются изобарно-изотермический и изохорно-изотермический процессы?

4. Сформулируйте первое начало термодинамики.

5. При каких условиях тепловой эффект процесса будет: а) равен изменению энтальпии этого процесса; б) равен изменению внутренней энергии процесса?

6. Химическая реакция протекает в герметичном реакторе. Изменением какой функции состояния будет определяться тепловой эффект реакции?

7. В ходе химической реакции температура системы повышается. Является этот процесс экзотермическим или эндотермическим? Какой знак (+) или (-) имеет изменение энтальпии этого процесса?

8. Сформулируйте закон Гесса.

9. Дайте определение понятия «стандартная энтальпия образования вещества».

10. Чему равны стандартные энтальпии образования молекулярного хлора и устойчивой при температуре 298 К модификации железа α-Fe?

11. Стандартная энтальпия образования белого фосфора равна нулю, а красного– (-18,41) кДж/моль. Какая из аллотропных модификаций более устойчива при температуре 25 ^оС?

12. Сформулируйте 1-е следствие закона Гесса.

13. Дайте определение понятия «стандартная энтальпия сгорания вещества».

14. Как связаны между собой стандартная энтальпия образования углекислого газа и стандартная энтальпия сгорания устойчивой при Т=298 К модификации углерода – графита?

15. Приведите 3 примера самопроизвольно протекающих химических процессов.

16. Перечислите признаки химического (истинного) равновесия.

17. Приведите примеры процессов, сопровождающихся: а) увеличением энтропии; б)уменьшением энтропии.

18. Какой знак должно иметь изменение энтропии самопроизвольно протекающей реакции, если Δ_rН=0?

19. Какой знак должно иметь изменение энтропии реакции термического разложения карбоната кальция? Почему? Напишите уравнение реакции.

20. Какие термодинамические свойства участников реакции необходимо знать для решения вопроса о возможности протекания реакции?

21. Экзотермическая реакция между газами сопровождается увеличением объёма. Что можно сказать о возможности протекания такой реакции?

22. В каком из следующих случаев возможна смена направления протекания реакция при изменении температуры: а)DH<0, DS<0; б) DH>0, DS>0; в) DН<0, DS>0; г) DH>0, DS<0?

23. Найдите стандартную энтальпию реакции окисления газообразного оксида серы(IV) <