Макарова Т.П., Будкевич Р.Л.

УДК 54

Макарова Т.П., Будкевич Р.Л.

М 15Физическая и коллоидная химия: Методические указания по выполнению контрольной работы по дисциплине «Физическая и коллоидная химия» для бакалавров направления 131000 «Нефтегазовое дело» очной и очно-заочной форм обучения. – Альметьевск: Альметьевский государственный нефтяной институт, 2014. – 48с.

Методические указания предназначены для выполнения контрольной работы, подготовки к сдаче зачёта по дисциплине «Физическая и коллоидная химия» и полностью соответствуют программе курса для технических направлений и специальностей вуза.

В методических указаниях приведены: примеры решения задач; задачи для самостоятельного решения; список рекомендованной литературы (основной и дополнительный).

Необходимый справочный материал для расчётов приведен в соответствующих приложениях, ссылка на которые дается в методических указаниях по их выполнению.

Печатается по решению учебно-методического совета АГНИ.

Рецензенты:

Марданова Э.И. - к.т.н., доцент, зав. кафедрой прикладной химии АГНИ

Вахитова Р.И. - к.т.н, доцент, кафедры промышленной теплоэнергетики АГНИ

© Альметьевский государственный

нефтяной институт, 2014

Содержание

Общие указания…………………………………………………………………….4

Варианты контрольных заданий…………………………….………………….5

Тема 1.

Агрегатные состояния вещества. Фазовые равновесия. Фазовые переходы. Правило фаз.

1.1. Фазовые равновесия. Правило фаз…………………………………...................6

1.2. Диаграммы состояний…………………………………………………….……..7

1.3. Перегонка растворов. ……………..………………………………………….12

1.4. Закон распределения. Экстракция…………………………………… ……..14

Тема 2.

Растворы – физико-химические системы. Коллигативные свойства растворов.

2.1. Растворимость………………………………………………………...…….….16

2.2. Физико-химические свойства разбавленных растворов

неэлектролитов…………………………………………………….………………..17

2.3. Растворы сильных электролитов……………………….………………………21

2.4. Буферные растворы. Буферная ёмкость ……………………………………..23

2.5. Потенциометрическое и кондуктометрическое титрование………...………28

Тема 3.

Дисперсные системы. Оптические и электрокинетические свойства. Строение мицелл. ККМ в растворах……………………………………….…..33

Тема 4.

Поверхностные явления. Сорбция. Классификация сорбционных явлений. Механизмы процессов сорбции…...……………………………….... 36

Тема 5.

Устойчивость коллоидных растворов. Коагуляция. Седименция….……………………………………………………………….........................41

Приложение……………………………………………………………………….46

Образец заполнения титульного листа………………………………………...47

Список литературы.................................................................................................48

ОБЩИЕ УКАЗАНИЯ

Настоящие методические указания предназначены для выполнения контрольной работы, подготовки к сдаче зачёта по дисциплине «Физическая и коллоидная химия». Содержание и объём требований определяется программой дисциплины «Физическая и коллоидная химия».

При оформлении контрольной работы следует придерживаться следующих правил:

- все задачи должны строго соответствовать варианту;

- условия задач должны быть переписаны в тетрадь полностью;

- решения задач должны содержать краткие объяснения и комментарии к выполненным арифметическим действиям, ссылки на использованные при решении законы и правила;

- необходимо пользоваться современной научной химической номенклатурой;

- все величины должны быть выражены в единицах международной системы (СИ);

- на каждой странице необходимо оставлять поля для замечаний рецензента;

- каждая задача записывается с новой страницы.

- построение графиков, предусмотренное при решении задач, должно быть осуществлено на миллиметровой бумаге.

Номер варианта соответствует порядковому номеру в журнале группы.

Прежде чем приступать к решению той или иной задачи, следует изучить теоретические основы данного раздела и усвоить тот объём теоретического материала, который необходим для осознанного решения задачи. Полезно ознакомиться с решениями типовых задач и примеров, приведенными в пособии.

Выполненную контрольную работу следует направить на кафедру прикладной химии. Получив проверенную работу, в случае необходимости нужно исправить допущенные ошибки в той же тетради и сдать её на повторное рецензирование.

Варианты контрольных заданий

вариант	Номера задач
	1, 31, 61, 91, 121,151,181, 211, 241, 271, 301, 331, 361, 391, 421
	2, 32, 62, 92, 122, 152, 182, 212, 242, 272, 302, 332, 362, 392, 422
	3, 33, 63, 93, 123, 153, 183, 213, 243, 273, 303 ,333, 363, 393, 423
	4, 34, 64, 94, 124, 154, 184, 214, 244, 274, 304, 334, 364, 394, 424
	5, 35, 65, 95, 125, 155, 185, 215, 245, 275, 305, 335, 365, 395, 425
	6, 36, 66, 96, 126, 156, 186, 216, 246, 276, 306, 336, 366, 396, 426
	7, 37, 67, 97, 127,157,187, 217, 247, 277, 307, 337, 367, 397, 427
	8, 38, 68 , 98, 128, 158, 188, 218, 248, 278, 308, 338, 368, 398, 428
	9, 39, 69, 99, 129, 159, 189, 219, 249, 279, 309, 339, 369, 399, 429
	10, 40, 70, 100, 130,160, 190, 220, 250, 280, 310, 340, 370, 400, 430
	11, 41, 71, 101, 131, 161, 191, 221, 251, 281, 311, 341, 371, 401, 431
	12, 42, 72, 102, 132, 162, 192, 222, 252, 282, 312, 342, 372, 402, 432
	13, 43, 73, 103, 133, 163, 193, 223, 253, 283, 313, 343, 373, 403, 433
	14, 44, 74, 104, 134, 164, 194, 224, 254, 284, 314, 344, 374, 404, 434
	15, 45, 75, 105, 135, 165, 195, 225, 255, 285, 315, 345, 375, 405, 435
	16, 46, 76, 106, 136, 166, 196, 226, 256, 286, 316, 346, 376, 406, 436
	17, 47, 77, 107, 137, 167, 197, 227, 257, 287, 317, 347, 377, 407, 437
	18, 48, 78, 108, 138, 168, 198, 228, 258, 288, 318, 348, 378, 408, 438
	19, 49, 79, 109, 139, 169, 199, 229, 259, 289, 319, 349, 379, 409, 439
	20, 50, 80, 110, 140, 170, 200, 230, 260, 290, 320, 350, 380, 410, 440
	21, 51, 81, 111, 141, 171, 201, 231, 261, 291, 321, 351, 381, 411, 441
	22, 52, 82, 112, 142, 172, 202, 232, 262, 292, 322, 352, 382, 412, 442
	23, 53, 83, 113, 143, 173, 203, 233, 263, 293, 323, 353, 383, 413, 443
	24, 54, 84, 114, 144, 174, 204, 234, 264, 294, 324, 354, 384, 414, 444
	25, 55, 85, 115, 145, 175, 205, 235, 265, 295, 325, 355, 385, 415, 445
	26, 56, 86, 116, 146, 176, 206, 236, 266, 296, 326, 356, 386, 416, 446
	27, 57, 87, 117, 147, 177, 207, 237, 267, 297, 327, 357, 387, 417, 447
	28, 58, 88, 118, 148, 178, 208, 238, 268, 298, 328, 358, 388, 418, 448
	29, 59, 89, 119, 149, 179, 209, 239, 269, 299, 329, 359, 389, 419, 449
	30, 61, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360, 390, 420, 450

Тема 1.

Агрегатные состояния вещества. Фазовые равновесия.

Фазовые переходы. Правило фаз.

Диаграммы состояний

Пример 1.По кривым охлаждения сплавов кадмия и висмута Cd – Bi

Рис. 1.1. Схема построения диаграммы состояния по данным термического анализа.

1. рассчитать, сколько килограммов и какой компонент выпадает из 3 кг жидкого расплава, содержащего 20 % висмута, если расплав охладить до 200°С;

2. определить при этой температуре состав жидкой фазы.

Решение:

1. На диаграмме (рис.1.1) находим точку, соответствующую составу 20% висмута и температуре 200°С. Для этого восстанавливаем перпендикуляр из точки на оси концентрации соответствующей содержанию висмута 20%, до пересечения с прямой, проходящей при температуре 200°С (точка О). Т. к. точка О лежит в области двухфазного состояния системы (расплав и твердые кристаллы кадмия), то, при заданных температуре и концентрации, кадмий будет выпадать из расплава. По правилу рычага определяем количество выпавшего кадмия. Для этого измеряем длины отрезков ОМ и ОN. Предположим, что первый равен 10 мм, а второй – 17 мм. Тогда, при общем весе расплава 3 кг, количество кадмия, выпавшего из расплава, будет равно:

кг

2. Для определения состава жидкой фазы при температуре 200°С опускаем из точки N перпендикуляр на ось концентраций. В нашем случае состав соответствует концентрации приблизительно 45% висмута.

Пример 2.По диаграмме плавкости системы, состоящей из воды и хлорида аммония Н₂О – NH₄Cl (рис. 1.2) определите:

Рис. 1.2.

1. Сколько хлорида аммония NH₄Cl содержалось в 750 г воды, если первые кристаллы льда появились при охлаждении раствора до –10°С?

2. Что произойдет с кусочком льда, если его бросить при –5°С в 15%-ый раствор хлорид аммония NH₄Cl?

3. Растворится ли кристалл хлорида аммония NH₄Cl при +10°С в 25%-ом растворе?

4. Какова растворимость хлорида аммония NH₄Cl в воде при +5°С (растворимость выразить в молях соли на 1000 г воды)?

5. Сколько воды нужно добавить к 100 г 25%-ного раствора хлорида аммония NH₄Cl охлажденного до –10°С, чтобы выпавший хлорид аммония NH₄Cl вновь растворился?

6. Сколько эвтектики получится из 500 г 5 %-ного раствора хлорида аммония NH₄Cl?

Решение:

1. По диаграмме, при –10°С лед начинает выделяться из 14%-ного раствора, следовательно, 750 г воды должны были составить 86%. Отсюда искомое количество хлорида аммония NH₄Cl равно:

г

2. Лед расплавиться, т.к. точка, изображающая состояние системы, лежит в области, где устойчивой является одна жидкая фаза.

3. Кристалл хлорида аммония NH₄Cl не может раствориться в 25%-ном растворе при +10°С, т.к. точка, изображающая состояние системы лежит в области, где устойчивыми являются две фазы: твердый хлорид аммония NH₄Cl и водный раствор хлорида аммония.

4. Линия ВС диаграммы является линией растворимости хлорида аммония NH₄Cl в воде. Из диаграммы растворимость хлорида аммония при +5°С равна 23%.

Растворимость, выраженная в молях хлорида аммония NH₄Cl (М = 53,3 г/моль) на 1000 г воды будет равна

моль/л

5. При –10°С растворимость хлорида аммония NH₄Cl равна 20%. В 100 г 25 %-ного раствора содержится 25 г NH₄Cl, который после разбавления должен составить 20%. Тогда общий вес раствора после разбавления будет равен

г

т.е. для растворения выпавшей соли нужно к взятым 100 г 25 %-ного раствора добавить 25 г воды.

6. По правилу рычага количество твердой фазы (тв), выделившейся к моменту достижения эвтектической температуры, относится к количеству оставшейся жидкости (ж), как отрезок fB к отрезку df, т.е.

Общее количество твёрдой и жидкой фаз равно 500

m_тв + m_ж = 500 Исключив m_тв, получаем

, отсюда m_ж = 139 г

Т.к. при эвтектической температуре устойчивым может быть только жидкий раствор эвтектического состава, целиком превращающийся в эвтектику, то искомое количество эвтектики тоже будет равно 139 г.

Задачи для самостоятельного решения

31 – 40.Определите (рис.1.3), какое вещество и в каком количестве можно извлечь из сплава массой m_c-ва кг, состоящего из хлорида натрия NaCl и хлорида кальция CaCl₂ в определённом процентном соотношении, охлаждением его от 800 до t °С. Определите, какое вещество и в каком количестве необходимо добавить, чтобы выпавшие кристаллы растворились.

№ задачи	CaCl2 (%)	NaCl, (%)	t°С	mc-ва (кг)	№ задачи	CaCl2 (%)	NaCl (%)	t°С	mc-ва (кг)
									3,5
				1,5
									4,5
				2,5
									5,5

Рис. 1.3

41 – 50.Определите с помощью диаграммы (рис.1.4) какую массу вещества 1 нужно прибавить к веществу 2 массой m₂ кг, чтобы понизить температуру его затвердевания до температуры t °С.

№ задачи	вещество 1	вещество 2	m2 (кг)	t°С	№ задачи	вещество 1	вещество 2	m2 (кг)	t°С
	KCl	LiCl				LiCl	KCl
	KCl	LiCl				LiCl	KCl
	KCl	LiCl				LiCl	KCl
	KCl	LiCl				LiCl	KCl
	KCl	LiCl				LiCl	KCl

Рис.1.4

Рис. 1.5

51 – 60. Определите с помощью диаграммы (рис. 1.5), какое вещество – кадмий или висмут (Cd или Вi) и в каком количестве выделяется из расплава массой m_р-ва определённой концентрации ω (по кадмию) при охлаждении его до температуры t°С. Определите с помощью диаграммы, сколько висмута Bi или Cd нужно прибавить, чтобы выпавший кадмий Cd или висмут Bi растворился.

№ задачи	mр-ва (г)	ω (%) Cd	t°С	№ задачи	mр-ва (г)	ω (%) Cd	t°С

Перегонка. Состав смеси

Пример 1.Рассчитайте, в каком весовом соотношении будут перегоняться вода и бромбензол, если при 95,25°С давление паров бромбензола равно 121 мм.рт.ст., а воды – 639 мм.рт.ст. Жидкости взаимонерастворимы.

Решение:

Молекулярная масса воды равна 18 г/моль, а бромбензола – 157г/моль. Для решения используем уравнение:

Т. о., отношение веса бромбензола к весу воды в дистилляте будут составлять 1,65. Т.е. на 100 кг перегнанной воды будет приходиться 165 кг бромбензола. Соотношение числа молей этих веществ составит 121 : 639 = 1 : 5, т.е. с 1 молем бромбензола будет перегоняться 5 молей воды.

Пример 2.Две жидкости А и В неограниченно растворимы друг в друге. Давление пара этой смеси при 150°С представляет линейную функцию от концентрации. Давление пара компонента А при этой температуре равно 800 мм. рт.ст., а компонента В – 500 мм. рт.ст. Вычислите отношение числа молей компонента А к числу молей компонента В в парах над смесью содержащей 5 мол.% компонента А. Определите состав смеси, кипящей при температуре 150°С под давлением 760 мм.рт.ст.

Решение:

а) для определения соотношения компонентов А и В в паровой фазе найдём значения парциальных давлений этих компонентов над смесью, состоящей из 95 мол.% вещества В и 5 мол.% вещества А.

Подставив Х_а = 0,05, Р_а = 800 мм.рт.ст и Р_в = 500 мм.рт.ст. получим:

Р_а = 0,005 × 800 = 40 мм.рт.ст. Р_в = 0,95 × 500 = 495 мм.рт.ст.

Соотношение числа молей компонентов в паровой фазе равно соотношению парциальных давлений этих компонентов.

Т.о. при температуре 150°С над жидкой смесью, состоящей из 95 мол.% вещества В и 5 мол.% вещества А, в паровой фазе на 100 молей вещества В приходится 8 молей вещества А. Общее давление пара над смесью сумме парциальных давлений компонентов: 40 + 495 = 535 мм.рт.ст.

б) мольную долю вещества А в смеси, кипящей под давлением 760 мм.рт.ст. определяем по уравнению:

Р = Х_а(Р_а – Р_в) + Р_в, 760 = Х_а (800 – 500) + 500,

1 – Х_а = 1 – 0,87 = 0,13

Следовательно, смесь, кипящая при температуре 150°С и давлении 760мм.рт.ст. содержит 0,87 мольных долей компонента (87 мол.%) А и 0,13 мольных долей (13 мол.%) компонента В.

Задачи для самостоятельного решения

61 – 70.Две жидкости А и В неограниченно растворимы друг в друге. Давление пара этой смеси при некоторой температуре представляет линейную функцию от концентрации. Давление пара компонента А при этой температуре равно Р_а мм. рт.ст., а компонента В – Р_в мм. рт.ст. Вычислите отношение числа молей компонента А к числу молей компонента В в парах над смесью содержащей ω_А, % (мол.) компонента А. Определите состав смеси, кипящей при данной температуре под давлением Р мм.рт.ст.

параметры	№ задачи
Ра, мм рт.ст.
Рв, мм рт.ст.
ωА, % (мол.)
Р мм.рт.ст.

71 - 80.При 250,9 мм. рт.ст. и 70°С жидкость, несмешивающаяся с водой, перегоняется с водяным паром. Вода при этой температуре имеет давление паров 233,7 мм.рт.ст. Полученный дистиллят содержит ω, % (масс.) жидкости. Вычислить молекулярную массу этой жидкости.

параметры	№ задачи
ω, % (масс.)	18,8	34,2	12,5	56,3	38,5	46,2	57,4	29,5	36,4	30,1

81 - 90.Температура кипения вещества А равна t₀ °С, а воды – 100°С. Вещество А и вода образуют азеотропную смесь состоящую из ω, % воды и вещества А. Температура кипения азеотропной смеси t°С. Определите, что останется в остатке, и что будет отгоняться при дистилляции смесей, содержащих:

а) ω₁, % воды; б) ω₂, % воды?

параметры	№ задачи
t0
ω, %
t
ω1, %
ω2, %

Тема 2.

Растворимость

Пример 1.Определение массы газа в растворе по его растворимости.

Сколько хлороводорода HCI растворится в 100 л воды при 40ºС и давлении 98625 Па, если растворимость HCI при этой температуре и давлении 1,0133×10⁵ Па составляет 386 м³ на 1 м³ воды?

Решение.

Растворимость (или коэффициент растворимости) выражают массой вещества (г), которое можно растворить в 100 г растворителя при данной температуре.

Определяем объём HCI, содержащегося в 100 л воды при 40ºС и давлении 1,0133×10⁵ Па:

1000 л H₂O — 386 м³

100 л H₂O — х м³ х = м³

Массу HCI вычисляем по уравнению Менделеева – Клайперона;

М (HCI) = 36,46 г/моль. Тогда:

m = = 53,4 кг.

Пример 2. Определение состава газовой смеси по растворимости газов.

Газовая смесь, содержащая 21% O₂ и 79% N₂, пропущена через воду при 0ºС и давлении 1,0133×10⁵ Па. Вычислите объёмные доли φ газовой смеси, растворённой в воде, если растворимость кислорода и азота в воде при этой температуре и давлении соответственно равна 0,048 и 0,0236 м³ на 1 м³ воды.

Решение.

Согласно закону Генри растворимость (Р) газа в воде пропорциональна его парциальному давлению в смеси. Определим парциальное давление газов в смеси:

p О₂ = 1,0133 × 10⁵ × 0,21 = 0,2128 × 10⁵ Па;

p = 1,0133 × 10⁵ × 0,79 = 0,8005 × 10⁵ Па.

Учитывая парциальные давления, определяем растворимость газов:

Р = = 0,0104 м³;

Р = = 0,0189 м³.

Общий объём азота и кислорода; 0,0104 + 0,0189 = 0,0293 м³. Тогда объёмная доля газов и смеси составит (%):

φ = 0,0104×100/0,0293 = 35,49; φ = 100,00 – 35,49 = 64,51.

Задачи для самостоятельного решения

121 - 130.В воде при 20ºС и общем давлении 2,5×10⁵ Па растворена газовая смесь, состоящая из О₂, N₂ и Cl₂. Объёмные доли этих газов в смеси соответственно равны ω (О₂), ω (N₂) и ω (Cl₂) %. Растворимость газов в 1 м³ воды (м³): РО₂ = 0,031; РN₂ = 0,016; РCl₂ = 2,299. Определите объёмные доли газов в газовой смеси, растворённой в воде.

параметры	№ задачи
ω (О2) %
ω (N2) %
ω (Cl2) %

131 - 140.В некотором объёме V₁ л воды растворен объём V₂ л вещества А при температуре t ºС и давлении Р Па. Определите массовую долю вещества А в полученном растворе.

параметры	№ задачи
V1, л (вода)	0,05	0,09	0,3	1,2	1,4	1,5	1,9	2,6	5,7	3,5
V2, л (в-во А)	4,9	6,3	10,5	2,7	3,1	9,7	8,5	10,2	11,6	13,4
в-во А	HCl	HCl	HCl	HBr	HBr	NH3	NH3	H2S	H2S	H2S
t, ºС
Р, Па×105	1,0	1,03	1,06	1,09	1,1	1,12	1,14	1,16	1,18	1,2

Физико-химические свойства

Решение.

По закону Рауля следует, что

Δt_зам = 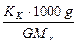; Δt_кип = ,

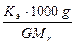где Δt_зам и Δt_кип – соответственно понижение температуры замерзания и повышение температуры кипения раствора; K_к и K_э – соответственно криоскопическая и эбуллиоскопическая константы растворителя; g – масса растворённого вещества, г; G – масса растворителя, г; M_r – молекулярная масса растворённого вещества; M_r(C₆H₅NO₂) = 123,11.

Повышение температуры кипения раствора нитробензола в бензоле :

Δt_кип = 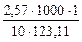= 2,09 ºС.

Температура кипения раствора: t_кип = 80,2 + 2,09 = 82,29 ºС.

Понижение температуры замерзания раствора нитробензола в бензоле:

Δt_зам = 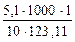= 4,14 ºС.

Температура замерзания раствора: Δt_зам = 5,4 – 4,14 = 1,26 ºС.

Пример 6. Вычисление молекулярной массы неэлектролита по повышению температуры кипения раствора.

Раствор камфоры массой 0,552 г в 17 г эфира кипит при температуре на 0,461 ºС выше, чем чистый эфир. Эбуллиоскопическая константа эфира 2,16ºС. Определите молекулярную массу камфоры.

Решение.

Молекулярную массу камфоры определяем, пользуясь соотношением

M_r = 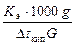= = 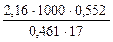155,14.

Молекулярная масса камфоры равна 155,14.

Задачи для самостоятельного решения

141 - 150. Осмотическое давление раствора, содержащего в объёме V₁ л массу m г неэлектролита, равно Р Па при температуре t ºС. Вычислите молекулярную массу неэлектролита.

параметры	№ задачи
V1, л
m, г	3,2	5,7	13,5	32,3	27,7	16,1	9,4	15,4	6,2	7,3
Р, Па×105	2,42	2,62	1,98	1,69	2,52	3,01	2,52	2,63	1,96	1,87
t, ºС

151 - 160. Давление водяного пара при температуре t ºС равно Р Па. Определите давление водяного пара над раствором, содержащим массу m₁ г некоторого вещества в массе m₂ г воды при этой температуре.

параметры	№ задачи
t, ºС
Р, Па	7375,9	4245,2					1227,8	2335,42	7375,9	4245,2
m1, г	6,2	9,4	8,7	20,4	3,5	8,3	3,5	7,4	2,5	9,6
m2, г
в-во	сахароза C12H22O11	этиленгликоль C2H4(OH)2	глюкоза C6H12O6	сахароза C12H22O11	глицерин C3H5(OH)3

161 - 170. Определите температуру кипения водного раствора некоторого вещества, если массовая доля его в растворе равна ω % (масс.). К_э(Н₂О) = 0,516

параметры	№ задачи
ω %, (масс.)
в-во	сахароза C12H22O11	этиленгликоль C2H4(OH)2	глюкоза C6H12O6	сахароза C12H22O11	глицерин C3H5(OH)3

171 - 180. Раствор неэлектролита массой m₁ г в воде массой m₂ г замерзает при температуре t ºС. Вычислите молекулярную массу неэлектролита. К_к(Н₂О) = 1,85.

параметры	№ задачи
m1, г	1,05	1,04	1,03	1,08	2,24	2,08	2,52	3,56	3,08	3,43
m2, г
t, ºС	–0,7	–0,6	–0,5	–0,8	–0,9	–0,4	–1,1	–1,2	–1,3	–1,4

Решение.

Изотонический коэффициент i показывает, во сколько раз значения осмотического давления р_осм, повышения температуры кипения Δt`<sub>кип</sub> (или понижения температуры замерзания Δt`_зам), понижения давления пара растворителя Δр` для раствора электролита, найденные экспериментально, больше соответствующих значений (Δр<sub>осм</sub>, Δt`_кип,Δt`_зам, Δр) для растворов неэлектролитов при той же молярной концентрации или молярности. Отклонение растворов электролитов от законов Вант-Гоффа и Рауля объясняется тем, что при растворении электролита в воде увеличивается общее число частиц, так как электролиты диссоциируют на ионы.

Значение изотонического коэффициента для растворов электролитов больше 1, а для растворов неэлектролитов равно 1. Осмотическое давление для растворов электролитов с учетем изотонического коэффициента равно:

р_осм = i .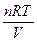

Отсюда:

i = 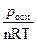= = 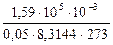= 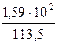1,4.

Пример 2. Вычисление изотонического коэффициента по давлению пара растворителя над раствором.

Давление водяного пара над раствором 24,8 г KCI в 100 г H₂O при 100ºС равно 9,14×10⁴ Па. Вычислите изотонический коэффициент, если давление водяного пара при этой температуре равно 1,0133×10⁵ Па.

Решение.

Первый закон Рауля для электролитов выражается уравнением:

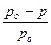= i ,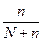

M (KCI) = 74,56 г/моль; n = 24,8/74,56 = 0,33 моль;

M(H₂O) = 18,02 г/моль; N = 100/18,02 = 5,55 моль.

Изотонический коэффициент равен:

i = 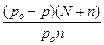= = 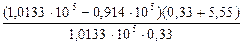= =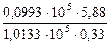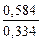1,75.

Пример 3. Вычисление кажущейся степени диссоциации сильного электролита по значению изотонического коэффициента.

Изотонический коэффициент 0,2н. раствора нитрата кальция Ca(NO₃)₂ равен 2,48. Вычислите кажущуюся степень диссоциации этого электролита.

Решение.

В случае сильных электролитов кажущуюся степень диссоциации определяют экспериментально, она всегда меньше истинной степени диссоциации, которая близка к единице. Степень диссоциации и изотонический коэффициент электролита связаны между собой соотношением

α = ,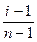

где n – число ионов, образующихся при диссоциации молекулы вещества.

При диссоциации Ca(NO₃)₂ образуется три иона. Кажущаяся степень диссоциации этого электролита равна

α = 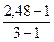= 1,48/2 = 0,74 (или 74%).

Пример 4. Вычисление степени диссоциации электролита по осмотическому давлению его раствора.

Рассчитайте кажущуюся степень электролитической диссоциации LiCI в 0,1 н. растворе соли, если раствор изотоничен с 0,19 М раствором сахара C₁₂H₂₂O₁₁ при 0ºС.

Решение.

Моль сахара равен 342,3 г. Осмотическое давление 0,19 М раствора сахара равно

p_{o cм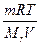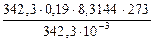} = = H/м² = 4,31·10⁵ Па.

M(LiCI) = 42,39 г/моль. По осмотическому давлению определяем изотонический коэффициент раствора LiCI:

i = 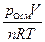= = 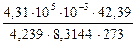1,9.

Кажущаяся степень диссоциации в 0,1 н. LiCI равна

α = 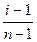= = 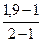= 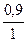0,9 (или 90%).

Задачи для самостоятельного решения

181 - 190. Изотонический коэффициент некоторого раствора электролит концентрацией С_м моль/л равен i. Сколько растворенных частиц содержится в объёме V л этого раствора?

параметры	№ задачи
в-во	HF	KCI	KNO3	KNO3	CaCI2	NaOH	MgCI2	HNO3	HCl	Ba(NO3)2
См моль/л	0,1	0,2	0,2	9×10-2	3,37	0,2	0,1		1,87	0,12
i	1,15	1,81	1,78	2,0	1,78	1,8	2,5	1,03	1,66	1,92
V, л	1,1	2,1	3,2	4,6	7,4	5,8	5,2	8,6	4,9	4,7

191 – 200.Осмотическое давление некоторого вещества концентрацией С_м моль/л при температуре t ºС равно р_осм Па. Вычислите изотонический коэффициент этого раствора.

параметры	№ задачи
См моль/л	0,1	0,05	0,06	0,07	0,08	0,09	0,11	0,12	0,13	0,14
t ºС		1,5		2,5		3,5		4,5		5,5
росм ×105Па	1,58	1,46	1,38	1,47	1,33	1,40	1,56	1,42	1,87	1,94

201 - 210. Рассчитайте кажущуюся степень диссоциации вещества в растворе концентрацией С_н моль/л, если изотонический коэффициент раствора данного вещества равен i. Вычислите осмотическое давление этого раствора при температуре t ºС.

параметры	№ задачи
в-во	KCI	KNO3	NaOH	MgCI2	HF	HNO3	HCl	Ba(NO3)2	KNO3	CaCI2
i	1,81	1,78	1,8	2,5	1,15	1,03	1,66	1,92	2,0	1,78
Сн моль/л	0,2	0,2	0,2	0,2	0,1		1,87	0,24	9×10-3	6,73
t ºС

Буферные растворы.

Пример 1.Вычисление рН буферного раствора.

1 л буферного раствора содержит 0,01 моль ацетата натрия и 0,1 моль уксусной кислоты. Найдите рН этого буферного раствора. Константа диссоциации уксусной кислоты равна Ксн₃соон = 1,75×10^-5.

Решение:

Буферными называют растворы, одновременно содержащие слабую кислоту и её соль (слабое основание и его соль) и обладающие свойством сохранять практически неизменной концентрацию ионов водорода при разбавлении, добавлении небольших количеств кислот или щелочей. Для любой слабой кислоты НА:

Кдис.кисл.	=	[Н+] [А-]	;	[Н+]	=	Ккисл [НА]	.
[НА]	[А-]

При добавлении к раствору слабой кислоты раствора сильного электролита (соли этой кислоты) концентрация аниона А^- значительно возрастает за счёт диссоциации соли. Так как сильные электролиты диссоциируют практически полностью, то концентрацию аниона А^- можно считать равной концентрации соли: [А^-] = [соли]. Концентрацию недиссоциированной части слабой кислоты можно приравнять к общей конце