Корпускулярно-волновой дуализм свойств материи

Впервые с проблемой двойственности природы материального объекта, волновой и корпускулярной, столкнулись при объяснении природы электромагнитного излучения. Как было показано раньше, существовал ряд экспериментов, которые хорошо объяснимы с позиций волновой природы электромагнитного излучения (например, интерференция и дифракция света). С другой стороны, существовали экспериментальные факты, объяснимые только с позиций корпускулярной природы света (фотоэффект, процессы излучения света нагретыми телами, Комптон-эффект). Так все же фотон – волна или частица?

Скорее всего, сущность этой проблемы связана с ограниченностью наших жизненных представлений. Мы живем в макромире, где только по отдельности встречаются процессы, имеющие корпускулярную и волновую природу. Нигде в повседневной жизни мы не встречаемся с движением, которое было бы результатом наложения этих двух форм, но это не значит, что его не существует. Из этой дилеммы возник совершенно новый подход к описанию физических и химических процессов микромира.

В 1924 г. Луи де Бройль (de Broglie) выдвинул гипотезу о том, что корпускулярно-волновой дуализм свойствен не только электромагнитному излучению, а является общим свойством материи. При этом он ввел понятие о волнах материи. Так, любому материальному объекту, обладающему массой m и движущемуся со скоростью v, соответствует волновой процесс с длиной волны l. По аналогии с электромагнитным излучением, где l=h/p, длина волны частицы (часто называется длиной волны де Бройля) вычисляется по уравнению

.

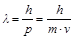Экспериментальное подтверждение волновых свойств электрона было получено в 1927 г. Девидсоном и Джермером и независимо от них Томсоном и Рейдом в опытах по рассеянию пучка электронов металлической фольгой.

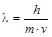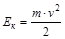Электроны, испускаемые нагретым катодом, разгоняются в электрическом поле напряжением » 100 В и приобретают кинетическую энергию » 100 эВ. При этом в случае, если формула де Бройля верна, электронам должна соответствовать длина волны .Если , то 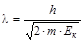. При E_к = 100 эВ (1 эВ=1,602×10^-19 Дж),l = 1,2 Å.

Если электроны обладают волновыми свойствами, то их пучок должен испытывать дифракцию на дифракционной решетке, постоянная которой a соизмерима с длиной волны электрона (a - постоянная решетки - сумма ширины щели и ширины промежутка между щелями). Так как длина волны электрона мала (l=1.2 Å), то роль дифракционной решетки, у которой a » l, могут играть кристаллические плоскости монокристаллов. В частности, была использована металлическая фольга (никель). Причем положение дифракционных полос должно определяться условием Вульфа-Брэгга: n×l = 2×a×sinJ (n - номер дифракционной полосы; l - длина волны электрона; a - постоянная дифракционной решетки; J - угол, под которым пучок электронов попадает на дифракционную решетку).

Действительно, при пропускании пучка электронов через металлическую фольгу была получена дифракционная картина в виде концентрических колец, положение которых изменялось в зависимости от кинетической энергии электронов (ускоряющего напряжения) – их длины волны, согласно условию Вульфа-Брэгга (рис. 1.2).

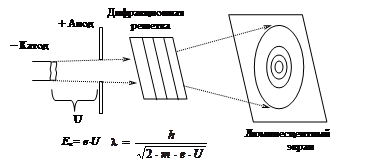Рис. 1.2. Схема опыта дифракции электронов: U (В) – напряжение ускоряющего электрического поля

Позднее наблюдали дифракцию и более тяжелых частиц, например протонов, нейтронов, атомов гелия.

Можно предположить, что и движению макрообъекта соответствует также волновой процесс. Движению тела массой m = 1 г со скоростью v = 1 см/с соответствует волновой процесс с длиной волны l=6,6×10^-29 м. Нет таких дифракционных решеток, чтобы наблюдать этот процесс.

Корпускулярно-волновой дуализм свойств электрона, как и других микрообъектов, является первым фундаментальным положением, на котором строится волновая механика – механика, применимая для описания объектов атомных и субатомных размеров.

Принцип неопределенности

Вторым фундаментальным положением, на котором строится волновая механика, является принцип неопределенности Гейзенберга. Поскольку электрон обнаруживает одновременно свойства волны и частицы, возникают трудности, связанные с измерением корпускулярных свойств электрона, а именно одновременного определения координат и импульса электрона.

Вернер Гейзенберг (Heisenberg) в 1927 г. сформулировал следующее положение: для микрочастицы невозможно одновременно точно определить ее координаты и импульс. Ограничения в точности определения даются соотношением Гейзенберга:

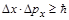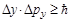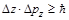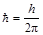, , , – постоянная Планка.

Из принципа неопределенности следует вероятностный подход к описанию механики микрообъектов. Точное определение координат частицы и ее импульса заменяется определением вероятности нахождения частицы в какой-то области пространства.Для движущейся частицы с вполне определенной энергией, а следовательно, импульсом мы не можем указать точные значения координат (траектории движения), а можем говорить лишь о вероятности нахождения ее в какой-либо части пространства.

Вероятностный характер механики микрочастиц следует также из опытов по дифракции электронов. Если пропускать не поток электронов, а последовательно по одному, то каждый электрон попадет в какое-то определенное место экрана и дифракционной картины не будет (от одного электрона). В какое конкретное место попадет следующий электрон, мы не знаем, но знаем, где вероятность его появления максимальна и где минимальна. И только большое число электронов, пропущенных последовательно друг за другом, создадут на экране дифракционную картину.